臺北市立永春高級中學 113 學年度數學教師甄試試題
一、 填充題:每題 8 分,共 88 分。 分數或根式須以最簡形式回答,否則不予計分。
解答:$$\cases{\alpha+\beta+ \gamma=5\\ \alpha\beta+ \beta\gamma+ \gamma\alpha =b\\ \alpha\beta \gamma=-c},又f(-1)=-6-b+c=20 \Rightarrow -b+c=26 \\ \Rightarrow \begin{vmatrix}1+\alpha & 1 & 1\\1 & 1+\beta & 1\\ 1 & 1& 1+\gamma \end{vmatrix} =\alpha\beta+ \beta\gamma+ \gamma\alpha +\alpha\beta \gamma=b-c= \bbox[red, 2pt]{-26}$$解答:$$3\log_{1/6} a+2\log_{1/6}b =\log_{1/6}a^3b^2 =-\log_6 a^3b^2= \color{blue}{\log_6(a^3b^2)^{-1}} \\ {1\over 2a}+{1\over 3b} \xrightarrow{要湊成三個a,二個b}{1\over 6a}+ {1\over 6a}+ {1\over 6a}+{1\over 6b}+{1\over 6b} \ge 5\sqrt[5]{({1\over 6})^5\cdot {1 \over a^3b^2}} ={5\over 6}(a^3b^2)^{-1/5} \\ \Rightarrow 30\ge {5\over 6}(a^3b^2)^{-1/5} \Rightarrow 6^2\ge (a^3b^2)^{-1/5} \Rightarrow 6^{10}\ge (a^3b^2)^{-1} \Rightarrow 10\ge \color{blue}{\log_6(a^3b^2)^{-1}} \\ \Rightarrow 3\log_{1/6} a+2\log_{1/6}b的最大值為\bbox[red, 2pt]{10}$$
解答:$$(1+2 +3+ 4+ 5+ 6+7+8)\cdot 2^7 = \bbox[red, 2pt]{4608}\\ \href{https://www.cpshs.hcc.edu.tw/resource/openfid.php?id=2035}{TRML 2013個人賽第一回第3題}$$
解答:$$|z|=1 \Rightarrow z=e^{i\theta} \Rightarrow |z^2-z+1|= \left|{1\over z} \right| \left|z-1+{1\over z} \right| =\left|z-1+{1\over z} \right| =|e^{i\theta}-1+e^{-i\theta}| =|2\cos \theta-1| \\ \Rightarrow \cases{M=3\\ m=0} \Rightarrow M+m= \bbox[red, 2pt]3$$
解答:$${總積分\over 隊數} ={1\cdot 20+ 2\cdot 15+ 4\cdot 10+8\cdot 5+ 16\cdot 3\over 32} ={178\over 32}=\bbox[red, 2pt]{89\over 16}$$
解答:$$\lim_{x\to \infty}{f(x)-2x^3\over x^2}=1 \Rightarrow f(x)=2x^3+x^2+ax+b, 又\lim_{x\to 0}{f(x)\over x}=-3 \Rightarrow a=-3,b=0 \\ \Rightarrow f(x)=2x^3+x^2-3x \Rightarrow f(3)=54+9-9=\bbox[red, 2pt]{54}$$
解答:$$題目應該是出錯了,只能硬著頭皮...\\ x^3-3x^2+5x=0 \Rightarrow x(x^2-3x+5)=0 \Rightarrow x=0 (x^2-3x+5=0無實根)\\ 因此x+y只要考慮y,即y^3-6y^2+10y-7=0無法因式分解,只能代公式\\y=\bbox[red, 2pt]{2+ \sqrt[3]{{3\over 2}+{1\over 6}\sqrt{211\over 3}}+\sqrt[3]{{3\over 2}-{1\over 6}\sqrt{211\over 3}}} \\ \href{https://zh.wikipedia.org/zh-tw/%E4%B8%89%E6%AC%A1%E6%96%B9%E7%A8%8B}{公式來源}$$
解答:$$\overline{AH} \bot \overline{BC} \Rightarrow \overrightarrow{AH} \cdot \overrightarrow{BC} =0 \Rightarrow \left( -{1\over 2}\overrightarrow{AB} +{3\over 2} \overrightarrow{AC}\right) \cdot (-\overrightarrow{AB} +\overrightarrow{AC}) =0 \Rightarrow {1\over 2}\cdot 5^2-2\overrightarrow{AB} \cdot \overrightarrow{AC}+{3\over 2}\cdot 3^2=0 \\ \Rightarrow \overrightarrow{AB} \cdot \overrightarrow{AC} =13 \Rightarrow \cos \angle A={\overrightarrow{AB} \cdot \overrightarrow{AC} \over |\overrightarrow{AB}| |\overrightarrow{AC}|} ={13\over 5\cdot 3} ={13\over 15} ={5^2+3^2-\overline{BC}^2 \over 2\cdot 3\cdot 5} \Rightarrow \overline{BC} =2\sqrt 2 \\ \Rightarrow {\overline{BC} \over \sin \angle A} =2R \Rightarrow {2\sqrt 2\over 2\sqrt{14}/15} =2R \Rightarrow R= {15\over 2\sqrt{7}} \Rightarrow R^2\pi= \bbox[red, 2pt]{{225\over 28} \pi}$$
解答:$$\sin^2 \theta={1\over 2}(1-\cos 2\theta) \Rightarrow \sin^2 50^\circ+\sin^2 70^\circ-\sin^2 80^\circ\\ ={1\over 2}(1-\cos 100^\circ)+{1\over 2}(1-\cos 140^\circ)-{1\over 2}(1-\cos 160^\circ)\\ ={1\over 2}(1+\cos 80^\circ)+{1\over 2}(1+\cos 40^\circ)-{1\over 2}(1+\cos 20^\circ)\\ =1+{1\over 2}(\cos 80^\circ+ \cos 40^\circ) -{1\over 2}(1+\cos 20^\circ) =1+\cos 60^\circ \cos20^\circ -{1\over 2}(1+\cos 20^\circ) \\=1+{1\over 2} \cos20^\circ-{1\over 2}-{1\over 2}\cos 20^\circ =\bbox[red, 2pt]{1 \over 2}$$
$$假設直線S在平面E上,且A,B,C在E上的投影點為A',B',C',如上圖。\\ 假設兩歪斜線的距離為a,則\cases{\overline{A'D}=\sqrt{100-a^2} \\ \overline{B'E} =\sqrt{169-a^2} \\ \overline{C'F} =\sqrt{576-a^2}} \Rightarrow \overline{B'E}={1\over 2}(\overline{A'D}+ \overline{C'F}) \\ \Rightarrow 4(169-a^2) =(\sqrt{100-a^2} +\sqrt{576-a^2})^2 =676-2a^2+2\sqrt{a^4-676a^2+57600} \\ \Rightarrow a^4 =a^4-676a^2+57600 \Rightarrow a^2={57600\over 676} ={14400\over 169} \Rightarrow a=\bbox[red, 2pt]{120\over 13}$$
解答:$$f(x)=3x^4-4mx^3+1 \Rightarrow f'(x)=12x^3-12mx^2=12x^2(x-m) \\ y=f(x)圖形為凹向上,f(x)=0無實根代表f'(x)=0的根其函數值皆大於0\\即f(0)f(m)\gt 0 \Rightarrow 1-m^4\gt 0 \Rightarrow \bbox[red, 2pt]{-1\lt m\lt 1}$$
二、 計算題:共 12 分。 須詳細過程,否則酌予扣分。
解答:$$\cases{\sqrt{10-6\cos \theta} =\sqrt{(\cos \theta-3)^2 +\sin^2\theta} \\{1\over 4} \sqrt{34-24\sqrt 2\sin \theta}= \sqrt{{17\over 8} -{3\over 2} \sqrt 2\sin \theta} =\sqrt{\cos^2 \theta-(\sin \theta-{3\over 4}\sqrt 2)^2} \\ \sqrt{19-2\sqrt 2\cos \theta-8\sin \theta} =\sqrt{(\cos \theta-\sqrt 2)^2 +(\sin \theta-4)^2}} \\ \Rightarrow 原式= \overline{PA}+ \overline{PB}+\overline{PC},其中\cases{P(\cos \theta, \sin \theta)在單位圓上\\ A(3,0)\\ B(0,3\sqrt 2/4) \\C(\sqrt 2,4)} \Rightarrow L= \overleftrightarrow{AB} :\sqrt 2x+4y=3\sqrt 2 \\ \Rightarrow 圓心O(0,0)至L距離=1 \Rightarrow 取切點為P =({1\over 3},{2\sqrt 2\over 3}),此時剛好O,P,C在一直線上\\ \Rightarrow \overline{PA}+ \overline{PB}+\overline{PC}=\overline{AB} +\overline{OC}-1= \sqrt{9+{18\over 16}} +\sqrt{18}-1= \bbox[red, 2pt]{{21\over 4}\sqrt 2-1}$$
========================== END ============================
解題僅供參考,其他教甄試題及詳解





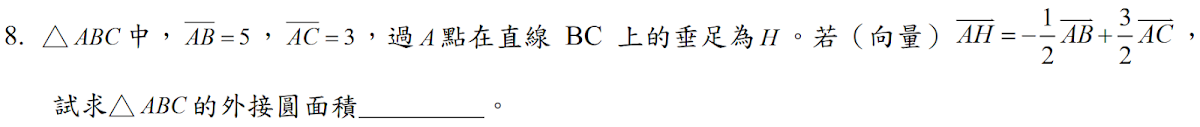






沒有留言:
張貼留言