新北市立國民中學 114 學年度教師聯合甄選數學科試題
選擇題: 共 40 題,總分 100 分。第 1~40 題,每題 2.5 分。
解答:$$\cases{12/4=3\\ 12\times 3/4=9} \Rightarrow \cases{Q_1=(a_3+a_4)/2=(3.2+3.4)/2=3.3\\ Q_3=(a_9+a_{10}) /2= (3.8+3.8)/2= 3.8} \\ \Rightarrow IQR=Q_3-Q_1=3.8-3.3=0.5,故選\bbox[red, 2pt]{(A)}$$解答:$$S=a_1+a_2+ \cdots+a_{10} =a(1+r+\cdots +r^9) =a\cdot {1-r^{10} \over 1-r} =4\cdot {1-1/1024\over 1/2} \\=8\cdot {1023\over 1024} \approx 8,故選\bbox[red, 2pt]{(D)}$$
解答:$$\cases{A(-1,3) \\B(2,7) \\C(5,3)} \Rightarrow a\triangle ABC= {1\over 2} \begin{Vmatrix} -1& 3& 1\\ 2& 7& 1\\ 5& 3& 1 \end{Vmatrix} ={1\over 2} \cdot |-24|=12,故選\bbox[red, 2pt]{(B)}$$
解答:$$只需考慮(A),(D) \Rightarrow \\\cases{(A)\bar x=(1+2+4+5+6)/5 =3.6 \Rightarrow \sum |x-\bar x|^2 =2.6^2+1.6^2+0.4^2+1.4^2+2.4^2\\ (D)\bar x=(1+4+6+8+9)/5=5.6 \Rightarrow \sum|x-\bar x|^2=4.6^2+1.6^2+0.4^2+2.4^2+3.4^2}\\ \Rightarrow 顯然(D)比較大,故選\bbox[red, 2pt]{(D)}$$
解答:$$4^{19} \times 5^{33} =2^{38} \times 5^{33} =2^5\times 10^{33} =32\times 10^{33}為35位數,故選\bbox[red, 2pt]{(B)}$$
解答:$${x+2\over x-3}\lt 2 \Rightarrow {x+2\over x-3}-2\lt 0 \Rightarrow {-x+8\over x-3} \lt 0 \Rightarrow (x-3)(-x+8)\lt 0 \Rightarrow (x-3)(x-8)\gt 0\\ \Rightarrow x\gt 8或x\lt 3,故選\bbox[red, 2pt]{(A)}$$
解答:$$連抽2球\cases{都是紅球機率=(5/9)(4/8) =5/18\\ 都是藍球機率=(4/9)(3/8)=1/6} \Rightarrow {5\over 18}+{1\over 6}={4\over 9},故選\bbox[red, 2pt]{(D)}$$
解答:$$\sqrt{64+32\sqrt 3}-\sqrt{97+56\sqrt 3} =\sqrt{64+ 2\sqrt {768}}-\sqrt{97+2\sqrt {2352}} =(\sqrt{48}+\sqrt{16})- (\sqrt{49}+\sqrt{48}) \\=4\sqrt 3+4-7-4\sqrt 3=-3,故選\bbox[red, 2pt]{(A)}$$
解答:$$(A)\bigcirc: a,b, c皆是3的倍數 \Rightarrow (a+b+c)是3的倍數\Rightarrow (a+b+c)^2是9的倍數 \\(B)\times \cases{a=15\\b=12\\ c=21} \Rightarrow a+b+c =48不是9的倍數\\ (C)\times \cases{a=15\\b=12\\ c=42} \Rightarrow a+b+c =69不是2的倍數\\ (D)\times \cases{a=15\\b=12\\ c=42} \Rightarrow a^2+b^2+c^2=2133 不是18的倍數\\,故選\bbox[red, 2pt]{(A)}$$
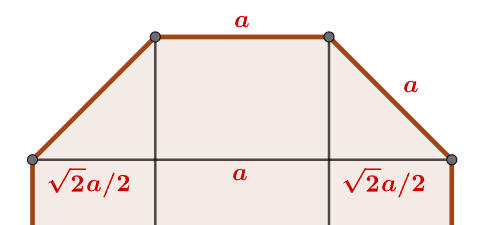
解答:
$$假設正八邊形邊長為a, 每一內角為{(8-2)\cdot 180\over 8}=135^\circ\\ \Rightarrow a+{\sqrt 2\over 2} a+{\sqrt 2\over 2} a=2 \Rightarrow a={2\over 1+\sqrt 2} =2(\sqrt 2-1),故選\bbox[red, 2pt]{(D)}$$
解答:$${1\over 2}+{1\over 4}+\cdots +{1\over 12} ={1\over 10}+{12+6+4+3+2\over 24} = {1\over 10}+{27\over 24} ={1\over 10}+1+{1\over 8} \\ \Rightarrow 需刪除{1\over 10}及{1\over 8},故選\bbox[red, 2pt]{(D)}$$
解答:$$依題意:5人=3男+1女+1師或3男+2女,因此有C^6_3C^4_1C^2_1+ C^6_3C^4_2 =160+120 =280\\,故選\bbox[red, 2pt]{(B)}$$
解答:$$y=f(x)={3x+2\over x-1} \Rightarrow 3x+2=xy-y \Rightarrow x(y-3)=y+2\Rightarrow x={y+2\over y-3},故選\bbox[red, 2pt]{(A)}$$
解答:$$\cases{x\ge 3 \Rightarrow |x-5|=1 \Rightarrow \cases{x\ge 5 \Rightarrow x-5=1\Rightarrow x=6\\ 3\le x\le 5 \Rightarrow 5-x=1 \Rightarrow x=4 }\\ x\le 3\Rightarrow |1-x| =1 \Rightarrow \cases{x\le 1\Rightarrow 1-x=1 \Rightarrow x=0\\ 1\le x\le 3 \Rightarrow x-1=1 \Rightarrow x=2}} \\ \Rightarrow x=0,2,4,6,共四個解,故選\bbox[red, 2pt]{(D)}$$
解答:$$\log_2 (x+3)+\log_2(x-4)= \log_2[(x+3)(x-4)]=3 \Rightarrow (x+3)(x-4)=2^3=8\\ \Rightarrow x^2-x-20=0 \Rightarrow (x-5)(x+4) =0 \Rightarrow x=5 (x=-4不合,違反x-4\gt 0),故選\bbox[red, 2pt]{(C)}$$
解答:$$\begin{cases}\sqrt{x+1}=2 & x\le 3\\ 3x-2=2& x\gt 3 \end{cases} \Rightarrow \cases{x=3\\ x=4/3違反x\gt 3},故選\bbox[red, 2pt]{(A)}$$
解答:$$\sin 330^\circ \times \tan(-585^\circ)+ \cos 930^\circ\times \tan 420^\circ =-\sin 30^\circ \times \tan 45^\circ+(-\cos 30^\circ)\times \tan 60^\circ \\=-{1\over 2}\times (-1)-{\sqrt 3\over 2}\times \sqrt 3={1\over 2}-{3\over 2}=-1,故選\bbox[red, 2pt]{(B)}$$
解答:$$(B)\times: rank(A)=n \Rightarrow A^{-1}存在 \Rightarrow \det(A)\ne 0 \\(C) \times:\det(A)=\det(A^t) \\(D)\times: AA^{-1}=I \Rightarrow \det(AA^{-1}) =\det(A)\det(A^{-1})=1 \Rightarrow \det(A^{-1}) =1/\det(A)\\,故選\bbox[red, 2pt]{(A)}$$
解答:$$f(x)=ax^2+bx +c \Rightarrow \cases{f(x+1)-f(x) =2ax+a+b\\ f(x+2)-f(x+1)=2ax+3a+b \\f(x+3)-f(x+2)=2ax +5a +b} \\\Rightarrow \cases{f(2024)-f(2023)=4-2=2=2a\cdot 2023+ a+b \\f(2025)-f(2024)=7-4=3 =2a\cdot 2023 +3a+ b \\ f(2026)-f(2025)=f(2026)-7=2a\cdot 2023+5a+b} \Rightarrow \cases{a=1/2\\ b=-4043/2} \\ \Rightarrow f(2026)=7+ 2023+ {5\over 2}- {4043\over 2} =11,故選\bbox[red, 2pt]{(C)}$$
解答:$$\cases{x=5 \Rightarrow \cases{3^{x+1}=3^6=729\\ 2^{2x-1} =2^9=512} \\x=6 \Rightarrow \cases{3^{x+1}=3^7= 2187\\ 2^{2x-1}=2^{11}= 2048} \\x=7 \Rightarrow \cases{3^{x+1}=3^8=6561\\ 2^{2x-1} =2^{13}=8192} \\x=8\cdots} \Rightarrow x=6兩式比較接近,故選\bbox[red, 2pt]{(B)}$$
解答:$$g(x-2)-1=f(x) \Rightarrow 向右2單位再向下1單位,故選\bbox[red, 2pt]{(A)}$$
解答:$$P=(x+y=7) \cap (2x-y=5) =(4,3) \\ L垂直4x+3y=10 \Rightarrow L:3x-4y=k,又通過Q(1,2) \Rightarrow k=-5\\ \Rightarrow d((4,3),3x-4y+5=0) ={5\over 5}=1,故選\bbox[red, 2pt]{(A)}$$
解答:$$\cases{a=2b+c\\ b=2c+d\\ 2c=d+a+ 1\\ d=a-c} \Rightarrow \cases{b=2c+d\\ 2c=d+2b+c+1\\ d=2b+c-c} \Rightarrow \cases{b=2c+d\\ c=d+2b+1\\ d=2b} \Rightarrow b=2(d+2b+1)+2b \\ \Rightarrow b=2(2b+2b+1)+2b=8b+2+2b \Rightarrow 9b=-2 \Rightarrow b=-{2\over 9},故選\bbox[red, 2pt]{(D)}$$
解答:$$2\log(a-2b) =\log a+ \log b \Rightarrow \log(a-2b)^2=\log ab \Rightarrow (a-2b)^2=ab\\ \Rightarrow a^2-5ab+4b^2=0 \Rightarrow (a-4b)(a-b)=0 \Rightarrow a=4b (a\gt 2b \Rightarrow a-b\ne 0) \\ \Rightarrow {a-b\over a+b}={4b-b\over 4b+b}={3\over 5},故選\bbox[red, 2pt]{(C)}$$
解答:$$\cases{x=10a+d\\ y=10b+d\\ z=100c+10c+ c} \Rightarrow z=xy \Rightarrow 100c+10c+c=100ab+10(ad+bd)+d^2\\ \Rightarrow c 是一個完全平方數\Rightarrow c=1,4,9 \Rightarrow \cases{111=3\times 37 非兩個二位數相乘\\ 444=12\times 37兩個二位數的個位數字不同 \\ 999=27\times 37}\\ \Rightarrow \cases{(a,b,c,d) =(2,3,9,7) \\ (a,b,c,d)=(3,2,9,7)} \Rightarrow a+b+c+d= 21,故選\bbox[red, 2pt]{(A)}$$
解答:$$\cases{a+1/b=1 \\b+1/c=2\\ c+1/a=5} \Rightarrow c=5-{1\over a}={5a-1\over a} \Rightarrow b=2-{1\over c} =2-{a\over 5a-1} ={9a-2\over 5a-1} \\ \Rightarrow a+{5a-1\over 9a-2}=1 \Rightarrow 81a^2-54a+9=0 \Rightarrow 9(3a-1)^2=0 \Rightarrow a={1\over 3 } \Rightarrow c=2\Rightarrow b={3\over 2} \\ \Rightarrow abc={1\over 3}\cdot {3\over 2}\cdot 2=1 \Rightarrow \sqrt{abc}=1,故選\bbox[red, 2pt]{(C)}$$
解答:$$ab=8 \Rightarrow a^2b+ab^2+a+b=ab(a+b)+(a+b)=(ab+1)(a+b)=9(a+b)=81 \Rightarrow a+b=9 \\ \Rightarrow (a+b)^2=a^2+b^2+2ab=81 \Rightarrow a^2+b^2=81-2\cdot 8=65,故選\bbox[red, 2pt]{(C)}$$
解答:
解答:$${1\over 2}+{1\over 4}+\cdots +{1\over 12} ={1\over 10}+{12+6+4+3+2\over 24} = {1\over 10}+{27\over 24} ={1\over 10}+1+{1\over 8} \\ \Rightarrow 需刪除{1\over 10}及{1\over 8},故選\bbox[red, 2pt]{(D)}$$
解答:$$依題意:5人=3男+1女+1師或3男+2女,因此有C^6_3C^4_1C^2_1+ C^6_3C^4_2 =160+120 =280\\,故選\bbox[red, 2pt]{(B)}$$
解答:$$y=f(x)={3x+2\over x-1} \Rightarrow 3x+2=xy-y \Rightarrow x(y-3)=y+2\Rightarrow x={y+2\over y-3},故選\bbox[red, 2pt]{(A)}$$
解答:$$\cases{x\ge 3 \Rightarrow |x-5|=1 \Rightarrow \cases{x\ge 5 \Rightarrow x-5=1\Rightarrow x=6\\ 3\le x\le 5 \Rightarrow 5-x=1 \Rightarrow x=4 }\\ x\le 3\Rightarrow |1-x| =1 \Rightarrow \cases{x\le 1\Rightarrow 1-x=1 \Rightarrow x=0\\ 1\le x\le 3 \Rightarrow x-1=1 \Rightarrow x=2}} \\ \Rightarrow x=0,2,4,6,共四個解,故選\bbox[red, 2pt]{(D)}$$
解答:$$\log_2 (x+3)+\log_2(x-4)= \log_2[(x+3)(x-4)]=3 \Rightarrow (x+3)(x-4)=2^3=8\\ \Rightarrow x^2-x-20=0 \Rightarrow (x-5)(x+4) =0 \Rightarrow x=5 (x=-4不合,違反x-4\gt 0),故選\bbox[red, 2pt]{(C)}$$
解答:$$\begin{cases}\sqrt{x+1}=2 & x\le 3\\ 3x-2=2& x\gt 3 \end{cases} \Rightarrow \cases{x=3\\ x=4/3違反x\gt 3},故選\bbox[red, 2pt]{(A)}$$
解答:$$\sin 330^\circ \times \tan(-585^\circ)+ \cos 930^\circ\times \tan 420^\circ =-\sin 30^\circ \times \tan 45^\circ+(-\cos 30^\circ)\times \tan 60^\circ \\=-{1\over 2}\times (-1)-{\sqrt 3\over 2}\times \sqrt 3={1\over 2}-{3\over 2}=-1,故選\bbox[red, 2pt]{(B)}$$
解答:$$(B)\times: rank(A)=n \Rightarrow A^{-1}存在 \Rightarrow \det(A)\ne 0 \\(C) \times:\det(A)=\det(A^t) \\(D)\times: AA^{-1}=I \Rightarrow \det(AA^{-1}) =\det(A)\det(A^{-1})=1 \Rightarrow \det(A^{-1}) =1/\det(A)\\,故選\bbox[red, 2pt]{(A)}$$
解答:$$f(x)=ax^2+bx +c \Rightarrow \cases{f(x+1)-f(x) =2ax+a+b\\ f(x+2)-f(x+1)=2ax+3a+b \\f(x+3)-f(x+2)=2ax +5a +b} \\\Rightarrow \cases{f(2024)-f(2023)=4-2=2=2a\cdot 2023+ a+b \\f(2025)-f(2024)=7-4=3 =2a\cdot 2023 +3a+ b \\ f(2026)-f(2025)=f(2026)-7=2a\cdot 2023+5a+b} \Rightarrow \cases{a=1/2\\ b=-4043/2} \\ \Rightarrow f(2026)=7+ 2023+ {5\over 2}- {4043\over 2} =11,故選\bbox[red, 2pt]{(C)}$$
解答:$$\cases{x=5 \Rightarrow \cases{3^{x+1}=3^6=729\\ 2^{2x-1} =2^9=512} \\x=6 \Rightarrow \cases{3^{x+1}=3^7= 2187\\ 2^{2x-1}=2^{11}= 2048} \\x=7 \Rightarrow \cases{3^{x+1}=3^8=6561\\ 2^{2x-1} =2^{13}=8192} \\x=8\cdots} \Rightarrow x=6兩式比較接近,故選\bbox[red, 2pt]{(B)}$$
解答:$$g(x-2)-1=f(x) \Rightarrow 向右2單位再向下1單位,故選\bbox[red, 2pt]{(A)}$$
解答:$$P=(x+y=7) \cap (2x-y=5) =(4,3) \\ L垂直4x+3y=10 \Rightarrow L:3x-4y=k,又通過Q(1,2) \Rightarrow k=-5\\ \Rightarrow d((4,3),3x-4y+5=0) ={5\over 5}=1,故選\bbox[red, 2pt]{(A)}$$
解答:$$\cases{a=2b+c\\ b=2c+d\\ 2c=d+a+ 1\\ d=a-c} \Rightarrow \cases{b=2c+d\\ 2c=d+2b+c+1\\ d=2b+c-c} \Rightarrow \cases{b=2c+d\\ c=d+2b+1\\ d=2b} \Rightarrow b=2(d+2b+1)+2b \\ \Rightarrow b=2(2b+2b+1)+2b=8b+2+2b \Rightarrow 9b=-2 \Rightarrow b=-{2\over 9},故選\bbox[red, 2pt]{(D)}$$
解答:$$2\log(a-2b) =\log a+ \log b \Rightarrow \log(a-2b)^2=\log ab \Rightarrow (a-2b)^2=ab\\ \Rightarrow a^2-5ab+4b^2=0 \Rightarrow (a-4b)(a-b)=0 \Rightarrow a=4b (a\gt 2b \Rightarrow a-b\ne 0) \\ \Rightarrow {a-b\over a+b}={4b-b\over 4b+b}={3\over 5},故選\bbox[red, 2pt]{(C)}$$
解答:$$\cases{x=10a+d\\ y=10b+d\\ z=100c+10c+ c} \Rightarrow z=xy \Rightarrow 100c+10c+c=100ab+10(ad+bd)+d^2\\ \Rightarrow c 是一個完全平方數\Rightarrow c=1,4,9 \Rightarrow \cases{111=3\times 37 非兩個二位數相乘\\ 444=12\times 37兩個二位數的個位數字不同 \\ 999=27\times 37}\\ \Rightarrow \cases{(a,b,c,d) =(2,3,9,7) \\ (a,b,c,d)=(3,2,9,7)} \Rightarrow a+b+c+d= 21,故選\bbox[red, 2pt]{(A)}$$
解答:$$\cases{a+1/b=1 \\b+1/c=2\\ c+1/a=5} \Rightarrow c=5-{1\over a}={5a-1\over a} \Rightarrow b=2-{1\over c} =2-{a\over 5a-1} ={9a-2\over 5a-1} \\ \Rightarrow a+{5a-1\over 9a-2}=1 \Rightarrow 81a^2-54a+9=0 \Rightarrow 9(3a-1)^2=0 \Rightarrow a={1\over 3 } \Rightarrow c=2\Rightarrow b={3\over 2} \\ \Rightarrow abc={1\over 3}\cdot {3\over 2}\cdot 2=1 \Rightarrow \sqrt{abc}=1,故選\bbox[red, 2pt]{(C)}$$
解答:$$ab=8 \Rightarrow a^2b+ab^2+a+b=ab(a+b)+(a+b)=(ab+1)(a+b)=9(a+b)=81 \Rightarrow a+b=9 \\ \Rightarrow (a+b)^2=a^2+b^2+2ab=81 \Rightarrow a^2+b^2=81-2\cdot 8=65,故選\bbox[red, 2pt]{(C)}$$
解答:
$$假設正方形ABCD邊長為a \Rightarrow \cases{a\triangle ABG=a(a+4)/2\\ a\triangle ADE=a(a-4)/2\\ a\triangle EFG=8} \\ \Rightarrow a\triangle AEG=a^2+4^2-{a(a+4)\over 2}-{a(a-4)\over 2}-8=a^2+16-a^2-8=8,故選\bbox[red, 2pt]{(C)}$$
解答:$$ab=888\cdots8\times 55\cdots 5=8(11\cdots 1)\times 5(11\cdots 1) =40\times (11\cdots1)^2 =10\times(22\cdots2)^2\\ \Rightarrow 9ab=10\times(66\cdots 6)^2 的數字和=(66\cdots 6)^2的數字和 =900\\{\color{red}證明:} \cases{6^2=36 \Rightarrow 數字和=9 =9\times 1\\ 66^2=4356 \Rightarrow 數字和=18 =9\times 2\\ 666^2= 443556 \Rightarrow 數字和=27 =9\times 3\\ \cdots \\\overbrace{66 \cdots 6^2}^{n個}的數字和= 9n} \Rightarrow \overbrace{66\cdots6}^{100個}的數字和=9\times 100=900\\,故選\bbox[red, 2pt]{(B)}$$
解答:$$\cos^2 80^\circ+ \cos^2160^\circ+ \cos80^\circ \cos160^\circ = \cos 80^\circ (\cos 80^\circ+ \cos 160^\circ) + \cos^2160^\circ \\= 2\cos 80^\circ \cos 120^\circ \cos 40^\circ + \cos^2 20^\circ = -\cos 80^\circ \cos 40^\circ + \cos^2 20^\circ \\=-{1\over 2}(\cos 120^\circ+ \cos 40^\circ) +{1\over 2}(\cos 40^\circ +1) ={1\over 4}-{1\over 2}\cos 40^\circ+{1\over 2}\cos 40^\circ+{1\over 2}={3\over 4},故選\bbox[red, 2pt]{(C)}\\ 此題與\href{https://chu246.blogspot.com/2025/05/114_16.html}{114年香山高中教甄}單選題第8題相同$$
解答:$$\cases{A_n(1/n,0) \\B_n(0,1/(n+1))} \Rightarrow S_n={1\over 2}\cdot {1\over n}\cdot {1\over n+1}={1\over 2}\left({1\over n}-{1\over n+1} \right) \\ \Rightarrow S_1+S_2+\cdots+S_{2025} ={1\over 2} \left({1\over 1}-{1\over 2}+ {1\over 2}-{1\over 3}+ \cdots +{1\over 2025}-{1\over 2026} \right) ={1\over 2} \left(1-{1\over 2026} \right) \\={2025\over 4052},故選\bbox[red, 2pt]{(B)}$$
解答:$$\tan 1^\circ \cdot \tan 2^\circ \cdot \tan 3^\circ \cdots \tan 89^\circ \\=[\tan 1^\circ \cdot \tan 2^\circ \cdots \tan 44^\circ] \cdot \tan 45^\circ \cdot [\tan(90^\circ-44^\circ)\cdot \tan(90^\circ-43^\circ) \cdots \tan (90^\circ-1^\circ)] \\=[\tan 1^\circ \cdot \tan 2^\circ \cdots \tan 44^\circ] \cdot \tan 45^\circ \cdot [\cot 44^\circ\cdot \cot 43^\circ \cdots \cot 1^\circ] \\= [\tan 1^\circ \cot 1^\circ] [\tan 2^\circ \cot 2^\circ] \cdots[\tan 44^\circ \cot 44^\circ] \tan 45^\circ 1\cdot 1\cdots 1=1 \\ \Rightarrow \log(\tan 1^\circ) +\log(\tan 2^\circ)+ \cdots+\log(\tan 89^\circ) =\log (\tan 1^\circ \cdot \tan 2^\circ \cdots \tan 89^\circ) \\=\log 1=0,故選\bbox[red, 2pt]{(B)}\\ 此題與\href{https://chu246.blogspot.com/2025/05/114_16.html}{114年香山高中教甄}單選題第6題相同$$
解答:$$(A)\times: f(x)=(ax+b)q(x)+r =a(x+{b\over a})q(x)+r \Rightarrow 商=a\cdot q(x) \\(B)\times: f(x)=(ax+b)q(x)+r \Rightarrow xf(x)=x(ax+b)q(x)+rx =x(ax+b)q(x)+{r\over a}(ax+b)-{rb\over a} \\ \qquad \Rightarrow xf(x)=(ax+b)(xq(x)+{r\over a})-{br\over a} \Rightarrow \cases{商:xq(x)+r/a\\ 餘式:-br/a} \\(C) \bigcirc: 見(B)\\ (D)\times: x^2f(x)=x^2(ax+b)q(x)+rx^2 =x^2(ax+b)q(x)+({r\over a}x-{br\over a^2})(ax+b)+{b^2r\over a^2} \\ \qquad \Rightarrow x^2f(x)=(ax+b)(x^2q(x)+{r\over a}x-{br\over a^2}) +{b^2r\over a^2} \Rightarrow \cases{商:x^2q(x)+rx/a-{br/a^2}\\餘:b^2r/a^2} \\,故選\bbox[red, 2pt]{(C)}\\ 此題與\href{https://chu246.blogspot.com/2025/05/114_16.html}{114年香山高中教甄}多選題第3題相同$$
解答:
解答:$$ab=888\cdots8\times 55\cdots 5=8(11\cdots 1)\times 5(11\cdots 1) =40\times (11\cdots1)^2 =10\times(22\cdots2)^2\\ \Rightarrow 9ab=10\times(66\cdots 6)^2 的數字和=(66\cdots 6)^2的數字和 =900\\{\color{red}證明:} \cases{6^2=36 \Rightarrow 數字和=9 =9\times 1\\ 66^2=4356 \Rightarrow 數字和=18 =9\times 2\\ 666^2= 443556 \Rightarrow 數字和=27 =9\times 3\\ \cdots \\\overbrace{66 \cdots 6^2}^{n個}的數字和= 9n} \Rightarrow \overbrace{66\cdots6}^{100個}的數字和=9\times 100=900\\,故選\bbox[red, 2pt]{(B)}$$
解答:$$\cos^2 80^\circ+ \cos^2160^\circ+ \cos80^\circ \cos160^\circ = \cos 80^\circ (\cos 80^\circ+ \cos 160^\circ) + \cos^2160^\circ \\= 2\cos 80^\circ \cos 120^\circ \cos 40^\circ + \cos^2 20^\circ = -\cos 80^\circ \cos 40^\circ + \cos^2 20^\circ \\=-{1\over 2}(\cos 120^\circ+ \cos 40^\circ) +{1\over 2}(\cos 40^\circ +1) ={1\over 4}-{1\over 2}\cos 40^\circ+{1\over 2}\cos 40^\circ+{1\over 2}={3\over 4},故選\bbox[red, 2pt]{(C)}\\ 此題與\href{https://chu246.blogspot.com/2025/05/114_16.html}{114年香山高中教甄}單選題第8題相同$$
解答:$$\cases{A_n(1/n,0) \\B_n(0,1/(n+1))} \Rightarrow S_n={1\over 2}\cdot {1\over n}\cdot {1\over n+1}={1\over 2}\left({1\over n}-{1\over n+1} \right) \\ \Rightarrow S_1+S_2+\cdots+S_{2025} ={1\over 2} \left({1\over 1}-{1\over 2}+ {1\over 2}-{1\over 3}+ \cdots +{1\over 2025}-{1\over 2026} \right) ={1\over 2} \left(1-{1\over 2026} \right) \\={2025\over 4052},故選\bbox[red, 2pt]{(B)}$$
解答:$$\tan 1^\circ \cdot \tan 2^\circ \cdot \tan 3^\circ \cdots \tan 89^\circ \\=[\tan 1^\circ \cdot \tan 2^\circ \cdots \tan 44^\circ] \cdot \tan 45^\circ \cdot [\tan(90^\circ-44^\circ)\cdot \tan(90^\circ-43^\circ) \cdots \tan (90^\circ-1^\circ)] \\=[\tan 1^\circ \cdot \tan 2^\circ \cdots \tan 44^\circ] \cdot \tan 45^\circ \cdot [\cot 44^\circ\cdot \cot 43^\circ \cdots \cot 1^\circ] \\= [\tan 1^\circ \cot 1^\circ] [\tan 2^\circ \cot 2^\circ] \cdots[\tan 44^\circ \cot 44^\circ] \tan 45^\circ 1\cdot 1\cdots 1=1 \\ \Rightarrow \log(\tan 1^\circ) +\log(\tan 2^\circ)+ \cdots+\log(\tan 89^\circ) =\log (\tan 1^\circ \cdot \tan 2^\circ \cdots \tan 89^\circ) \\=\log 1=0,故選\bbox[red, 2pt]{(B)}\\ 此題與\href{https://chu246.blogspot.com/2025/05/114_16.html}{114年香山高中教甄}單選題第6題相同$$
解答:$$(A)\times: f(x)=(ax+b)q(x)+r =a(x+{b\over a})q(x)+r \Rightarrow 商=a\cdot q(x) \\(B)\times: f(x)=(ax+b)q(x)+r \Rightarrow xf(x)=x(ax+b)q(x)+rx =x(ax+b)q(x)+{r\over a}(ax+b)-{rb\over a} \\ \qquad \Rightarrow xf(x)=(ax+b)(xq(x)+{r\over a})-{br\over a} \Rightarrow \cases{商:xq(x)+r/a\\ 餘式:-br/a} \\(C) \bigcirc: 見(B)\\ (D)\times: x^2f(x)=x^2(ax+b)q(x)+rx^2 =x^2(ax+b)q(x)+({r\over a}x-{br\over a^2})(ax+b)+{b^2r\over a^2} \\ \qquad \Rightarrow x^2f(x)=(ax+b)(x^2q(x)+{r\over a}x-{br\over a^2}) +{b^2r\over a^2} \Rightarrow \cases{商:x^2q(x)+rx/a-{br/a^2}\\餘:b^2r/a^2} \\,故選\bbox[red, 2pt]{(C)}\\ 此題與\href{https://chu246.blogspot.com/2025/05/114_16.html}{114年香山高中教甄}多選題第3題相同$$
解答:

$$假設\cases{\overline{EG} \bot \overline{AB}且\overline{EG}=h \\ a\triangle DEF=x} \Rightarrow \cases{a\triangle AFE= \overline{AF} \cdot h/2\\ a\triangle BFD = \overline{BF}\cdot h/2\\ a\triangle DEF=\overline{DE}\cdot h/2} \Rightarrow \triangle AFE: \triangle BFD:\triangle DEF=\overline{AF}:\overline{BF} :\overline{DE} \\ \Rightarrow {15\over \overline{AF}} ={9\over \overline{BF}} ={x\over \overline{DE}} \Rightarrow {x\over \overline{DE}} ={15+9\over \overline{AF}+ \overline{BF}} ={24\over \overline{AB}} \Rightarrow {\overline{DE} \over \overline{AB}} ={x\over 24}\\ 又\overline{DE} \parallel \overline{AB} \Rightarrow {\triangle CDE \over \triangle ABC}={32\over x+56} ={\overline{DE}^2 \over \overline{AB}^2} ={x^2\over 24^2} \Rightarrow x^3+56x^2=18432 \\\Rightarrow x^2(x+56)=16^2\cdot (16+56) \Rightarrow x=16 \Rightarrow {\triangle DEF \over \triangle ABC}={x\over x+56}={16\over 72} ={2\over 9},故選\bbox[red, 2pt]{(C)}\\ 此題與\href{https://www.sec.ntnu.edu.tw/uploads/asset/data/625640a6381784d09345bc2f/07-99058-%E4%B8%AD%E5%AD%B8%E7%94%9F%E9%80%9A%E8%A8%8A%E8%A7%A3%E9%A1%8C%E7%AC%AC75%E6%9C%9F%E9%A1%8C%E7%9B%AE%E5%8F%83%E8%80%83%E8%A7%A3%E7%AD%94%E5%8F%8A%E8%A9%95%E8%A8%BB(%E6%9C%88%E5%88%8A).pdf}{科學教育月刊第332期問題編號《7503》}相同$$
解答:$$\cases{x^3-y^3=(x-y)(x^2+xy+y^2) =7(x-y) \\ x^3+y^3=(x+y)(x^2-xy+y^2) =5(x+y)} \Rightarrow \cases{(x-y)(x^2+xy+y^2-7)=0\\ (x+y)(x^2-xy+y^2-5)=0} \\ 由於\cases{直線L_1:x=y\\ 直線L_2: x=-y\\ 斜橢圓\Gamma_1:x^2+xy+y^2=7\\ 斜橢圖\Gamma_2:x^2-xy+y^2=5} \Rightarrow \cases{L_1與\Gamma_2有兩個交點 \\ L_2與\Gamma_1 有兩個交點\\ \Gamma_1與\Gamma_2有四個交點 \\ L_1與L_2有1個交點(0,0)} \Rightarrow 共9個交點,故選\bbox[red, 2pt]{(D)}$$
解答:$$x^2-2x+1+4y^2+8y+4=11+5 \Rightarrow (x-1)^2+4(y+1)^2=16 \Rightarrow {(x-1)^2\over 16} +{(y+1)^2\over 4 }=1 \\ \Rightarrow \cases{a=4\\b =2} \Rightarrow {2b^2\over a} ={8\over 4}=2,故選\bbox[red, 2pt]{(A)}$$
解答:
解答:$$\cases{x^3-y^3=(x-y)(x^2+xy+y^2) =7(x-y) \\ x^3+y^3=(x+y)(x^2-xy+y^2) =5(x+y)} \Rightarrow \cases{(x-y)(x^2+xy+y^2-7)=0\\ (x+y)(x^2-xy+y^2-5)=0} \\ 由於\cases{直線L_1:x=y\\ 直線L_2: x=-y\\ 斜橢圓\Gamma_1:x^2+xy+y^2=7\\ 斜橢圖\Gamma_2:x^2-xy+y^2=5} \Rightarrow \cases{L_1與\Gamma_2有兩個交點 \\ L_2與\Gamma_1 有兩個交點\\ \Gamma_1與\Gamma_2有四個交點 \\ L_1與L_2有1個交點(0,0)} \Rightarrow 共9個交點,故選\bbox[red, 2pt]{(D)}$$
解答:$$x^2-2x+1+4y^2+8y+4=11+5 \Rightarrow (x-1)^2+4(y+1)^2=16 \Rightarrow {(x-1)^2\over 16} +{(y+1)^2\over 4 }=1 \\ \Rightarrow \cases{a=4\\b =2} \Rightarrow {2b^2\over a} ={8\over 4}=2,故選\bbox[red, 2pt]{(A)}$$
解答:
$$假設正方形邊長為2\Rightarrow \cases{\overline{BE} =\overline{EC}=1\\ \overline{DF} =\overline{FC}=1 } \Rightarrow \cases{\overline{AE}=\overline{AF} =\sqrt 5\\ \overline{EF} =\sqrt 2} \Rightarrow \cos \angle EAF ={5+5-2\over 2\cdot 5} ={4\over 5} \\ \Rightarrow \sin \angle EAF={3\over 5},故選\bbox[red, 2pt]{(B)}$$
解答:$$x^2+ax+b=0的二實根為\alpha,\beta \Rightarrow \cases{\alpha+\beta=-a\\ \alpha\beta=b} \Rightarrow \alpha^2+\beta^2=(\alpha+\beta)^2-2\alpha\beta =a^2-2b\ge 9 \\ \Rightarrow (a,b)=(4-6,1),(4-6,2) ,(4-6,3),(5-6,4), (5-6,5),(5-6,6),共有15個\\ \Rightarrow 機率={15\over 36} ={5\over 12},故選\bbox[red, 2pt]{(B)}$$
解答:$$\cases{E(1.5X)=1.5E(X) =1.5\times 57=85.5\\Var(1.5X)=1.5^2Var(X)=2.25Var(X)} ,故選\bbox[red, 2pt]{(C)}$$
解答:$$檢定統計量={\bar x-\mu\over \sigma/\sqrt n}={73.3-70\over 9/\sqrt{81}} =3.3,故選\bbox[red, 2pt]{(D)}$$
解題僅供參考,其他教甄試題及詳解
解答:$$x^2+ax+b=0的二實根為\alpha,\beta \Rightarrow \cases{\alpha+\beta=-a\\ \alpha\beta=b} \Rightarrow \alpha^2+\beta^2=(\alpha+\beta)^2-2\alpha\beta =a^2-2b\ge 9 \\ \Rightarrow (a,b)=(4-6,1),(4-6,2) ,(4-6,3),(5-6,4), (5-6,5),(5-6,6),共有15個\\ \Rightarrow 機率={15\over 36} ={5\over 12},故選\bbox[red, 2pt]{(B)}$$
解答:$$\cases{E(1.5X)=1.5E(X) =1.5\times 57=85.5\\Var(1.5X)=1.5^2Var(X)=2.25Var(X)} ,故選\bbox[red, 2pt]{(C)}$$
解答:$$檢定統計量={\bar x-\mu\over \sigma/\sqrt n}={73.3-70\over 9/\sqrt{81}} =3.3,故選\bbox[red, 2pt]{(D)}$$
解題僅供參考,其他教甄試題及詳解











































老師好,請問能詢問今年114新北資優數學嗎?謝謝!
回覆刪除題目在哪?
刪除https://career.ntpc.edu.tw/module/newtea/module/newtea/out-home/out-announce
回覆刪除在這個網站上,裡面試題,可能要找一下資優數學的科目,數學題從26題開始,謝謝老師
最近比較忙..... 題目太多....
刪除