109學年度身心障礙學生升學大專校院甄試試題
甄試類(群)組別:四技二專組
考試科目(編號):數學(B)
單選題,共 20 題,每題 5 分$$已知\cases{A(1,5) \\ B(-3,1) \\ C(x,y)},B為A,C的中點\Rightarrow \cases{-3=(1+x)/2 \\ 1=(5+y)/2} \Rightarrow \cases{x=-7 \\ y=-3} \Rightarrow x+y=-10\\,故選\bbox[red,2pt]{(A)} $$
解:
$$已知\cases{A(2,2) \\ B(3,1) \\ C(4,2)} \Rightarrow \cases{\overrightarrow{BA}= (-1,1) \\ \overrightarrow{BC} =(1,1)} \Rightarrow \cos \angle ABC =\cfrac{\overrightarrow{BA} \cdot \overrightarrow{BC}}{|\overrightarrow{BA}|| \overrightarrow{BC}|} = \cfrac{-1+1}{|\overrightarrow{BA}|| \overrightarrow{BC}|} =0,故選\bbox[red,2pt]{(B)}$$
解:$$\cases{\tan \theta =3 \\ \sin \theta<0} \Rightarrow \cases{\sin \theta=-3/\sqrt{10} \\ \cos \theta = -1/\sqrt{10}} \Rightarrow \sin \theta -\cos \theta = -\cfrac{3}{\sqrt{10}} + \cfrac{1}{\sqrt{10}} =-\cfrac{2}{\sqrt{10}} =-\cfrac{\sqrt{10}}{5}\\,故選\bbox[red,2pt]{(B)}$$
解:
$$\cases{2^a= {1\over \sqrt 2}\\ 4^b=2} \Rightarrow \cases{2^a= 2^{-1/2}\\ 2^{2b}=2} \Rightarrow \cases{a= -1/2 \\ b=1/2} \Rightarrow 8^{a+b} =8^0=1,故選\bbox[red,2pt]{(A)}$$
解:$$\cases{a=\log_2 3 \\ b=\log_4 27 = {\log_2 27 \over \log_2 4} ={3\log_2 3 \over 2\log_2 2} ={3\over 2}\log_2 3 \\ c=\log_8 9 = {\log_2 9 \over \log_2 8} = {2\log_2 3 \over 3\log_2 2} ={2\over 3}\log_2 3} \Rightarrow b>a>c ,故選\bbox[red,2pt]{(C)}$$
解:$$\cases{a_2= 3 \\ a_5= 7 } \Rightarrow \cases{a_1+d = 3 \\ a_1+4d = 7 } \Rightarrow \cases{a_1=5/3 \\ d=4/3} \Rightarrow a_{11} = a_1+10d = {5\over 3}+10\times {4\over 3} =15,故選\bbox[red,2pt]{(D)}$$
解:$$f(x)=ax^2+3x+1= p(x)(3x-1)+1 \Rightarrow f(1/3)={1\over 9}a+1+1=1 \Rightarrow a=-9,故選\bbox[red,2pt]{(A)}$$
解:$$\begin{vmatrix}a & 1 & 1\\ 1 & 0 & 1\\ a & 1 & a \end{vmatrix} =0+1+a-0-a-a= 1-a=a \Rightarrow a=1/2,故選\bbox[red,2pt]{( B)}$$
解:
$$\cases{f(x,y)=2x-3y+1 \\ g(x,y)=5x-y-2 \\ P(1,2)} \Rightarrow \cases{f(P)=2-6+1<0 \\ g(P)=5-2-2 >0},故選\bbox[red,2pt]{(B)} $$
解:
$$(\sqrt{109}-a+1)(\sqrt{109}+a-1) =(\sqrt{109}-(a-1))(\sqrt{109}+(a-1)) = 109-(a-1)^2=100 \\ \Rightarrow a-1=0 \Rightarrow (a-1)^2 =9 \Rightarrow a-1= \pm 3 \Rightarrow \cases{a=4 \\ a=-2(不合)},故選\bbox[red,2pt]{(D)}$$
解:
$$以頂點為直角的三角形有兩個,見上圖,因此共有6\times 2=12個直角三角形,故選\bbox[red,2pt]{(D)}$$
解:
$$x+y \le 20 \Rightarrow \begin{array}{ccc} x & y & 次數\\\hline 0 & 0-20 & 21 \\ 1 & 0-19 & 20 \\ 2 & 0-18 & 19 \\ \cdots \\ 19 & 0-1 & 2\\ 20 & 0 & 1 \\ \hline\end{array} \Rightarrow 共有1+2+\cdots + 21= 22\times {21 \over 2} = 231,故選\bbox[red,2pt]{(B)}$$
解:
$$\cases{十位數a \\ 個位數b \\ a>b} \Rightarrow \begin{array}{ccc} a & b & 次數\\\hline 1 & 0 & 1 \\ 2 & 0-1 & 2 \\ 3 & 0-2 & 3 \\ \cdots \\ 9 & 0-8 & 9 \\ \hline\end{array} \Rightarrow 共有1+2+\cdots + 9= 45, 故選\bbox[red, 2pt]{(D)}$$
解:
$$\cases{P(A)=1-P(3次都是反面) = 1-({1\over 2})^3= {7\over 8} \\P(B)=1/2} \Rightarrow P(B\mid A)=\cfrac{P(A\cap B)}{P(A)} = \cfrac{1/2}{7/8} =4/7\\,故選\bbox[red,2pt]{(D)}$$
解:
$$\begin{array}{cl|ccc}|x-y| & (x,y) & 次數 & 機率 & 期望值\\ \hline 0 & (0,0)-(6,6) & 6 & 6/36 &0\\ 1 & (2,1),(3,2),..,(6,5) &10 & 10/36 & 10/36\\ & (1,2),(2,3),..,(5,6) \\ 2 & (3,1),(4,2),(5,3),(6,4)& 8 & 8/36 & 16/36\\ & (1,3),(2,4),(3,5),(4,6) \\ \cdots & \cdots \\ 5 & (6,1) & 2 &2/36 & 10/36\\ & (1,6) \\\hline \end{array} \\\Rightarrow 期望值= 0\times {6\over 36} + 1\times {10\over 36} + 2\times {8\over 36} + 3\times {6\over 36} + 4\times {4\over 36} + 5\times {2\over 36} \\ ={1\over 36}(10+16+18+16+10) = 70/36 = 35/18,故選\bbox[red,2pt]{(A)}$$
解:
$$餘弦定理:\cos 60^\circ =\cfrac{3^2+5^2-x^2}{2\times 3\times 5} \Rightarrow \cfrac{1}{2}= \cfrac{34-x^2}{30} \Rightarrow 34-x^2=15 \Rightarrow x^2=19 \Rightarrow x=\sqrt{19}\\,故選\bbox[red,2pt]{(C)}$$
解:
$$y=2x^2-3x+4 = 2(x^2-{3\over 2}x+ ({3\over 4})^2)+4-{9\over 8} =2(x-{3\over 4})^2+{23 \over 8} \Rightarrow (x-{3\over 4})^2= 4\cdot {1\over 8}(y-{23\over 8}) \\ \Rightarrow \cases{頂點P({3\over 4},{23\over 8}) \\c=1/8} \Rightarrow 焦點F({3\over 4},{23\over 8}+{1\over 8}) =({3\over 4},3) =(a,b) \Rightarrow {b\over a}=3\times {4\over 3} =4,故選\bbox[red,2pt]{(B)}$$
解:
$$4y=x^2+x+6 \Rightarrow y={1\over 4}(x^2+x+6) \Rightarrow 當x=1時,y={1\over 4}(1+1+6)=2 \Rightarrow 切點為P(1,2)\\ 又y'={1\over 4}(2x+1) \Rightarrow y'(1)={1\over 4}(2+1) = {3\over 4} \Rightarrow 切線L的斜率為{3\over 4} \Rightarrow L:y-2={3\over 4}(x-1) \\ \Rightarrow 當y=0時, -2={3\over 4}(x-1) \Rightarrow x= -{5\over 3},故選\bbox[red,2pt]{(A)}$$
解:
$$x^2+4y^2=2x+4y \Rightarrow x^2-2x+1 +4y^2-4y+1 =2 \Rightarrow (x-1)^2+4(y-{1\over 2})^2=2 \\ \Rightarrow \cfrac{(x-1)^2}{(\sqrt 2)^2} +\cfrac{(y-1/2)^2}{({1\over \sqrt 2})^2}=1 \Rightarrow \cases{a=\sqrt 2\\ b={1\over \sqrt 2}} \Rightarrow 短軸長2b= \sqrt 2,故選\bbox[red,2pt]{(C)}$$
解:$$\int_1^3 [2f(x)+3]dx =2\int_1^3 f(x)\;dx +3\int_1^3 1\;dx = 2\times 5+3\times (3-1)=10+6=16,故選\bbox[red,2pt]{(C)}$$
-- end --



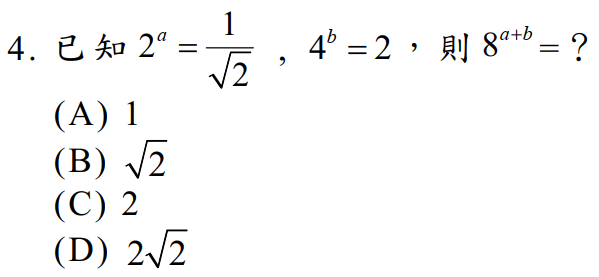

















沒有留言:
張貼留言