100年第二次國民中學學生基本能力測驗
試題來源:師大心測中心關鍵字:100年、國中、基測
解:$$L_1過圓心\Rightarrow d(O,L_1)=0\\ L_2與圓相交兩點且不過圓心\Rightarrow 0\lt d(O,L_2)\lt 半徑=20\\ L_3與圓不相交\Rightarrow d(O,L_3) \gt 半徑=20\\ L_4與圓相切\Rightarrow d(O,L_4)=半徑=20\\因此只有L_2與圓心距離可能為14,故選\bbox[red,2pt]{(B)}$$


解:$$\overline{AB} \parallel \overline{CD} \Rightarrow \cases{\angle BAO= \angle OCD\\ \angle ABO=\angle ODC} (內錯角相等) \Rightarrow \triangle OAB\sim \triangle OCD (AAA)\\ \Rightarrow {\overline{OA} \over \overline{OB}} ={\overline{OC} \over \overline{OD}} \Rightarrow {12/7 \over 18/7} ={10/3 \over \overline{OD}} \Rightarrow \overline{OD} ={10\over 3}\times {18\over 7} \times {7\over 12}=5 \Rightarrow C(0,5),故選\bbox[red,2pt]{(C)}$$
解:$$\cases{A(a,{29\over 4})\\ B(b,{29\over 4})} 皆在y=x^2+1上 \Rightarrow \cases{a^2+1= {29\over 4} \\b^2+1= {29\over 4} } \Rightarrow \cases{a=\sqrt{{29\over 4}-1}=\sqrt{25\over 4} ={5\over 2}\\b=-\sqrt{{29\over 4}-1}=-\sqrt{25\over 4} =-{5\over 2}} \\ \Rightarrow \overline{AB}=\sqrt{(a-b)^2+0^2} =\sqrt{({10\over 2})^2}=\sqrt{5^2} =5,故選\bbox[red,2pt]{(A)}$$
解:$$\cases{A(a,{29\over 4})\\ B(b,{29\over 4})} 皆在y=x^2+1上 \Rightarrow \cases{a^2+1= {29\over 4} \\b^2+1= {29\over 4} } \Rightarrow \cases{a=\sqrt{{29\over 4}-1}=\sqrt{25\over 4} ={5\over 2}\\b=-\sqrt{{29\over 4}-1}=-\sqrt{25\over 4} =-{5\over 2}} \\ \Rightarrow \overline{AB}=\sqrt{(a-b)^2+0^2} =\sqrt{({10\over 2})^2}=\sqrt{5^2} =5,故選\bbox[red,2pt]{(A)}$$
解:$$2-(3+3x) \lt 5-(2-x) \Rightarrow 2-3-3x \lt 5-2+x \Rightarrow -1-3x\lt 3+x \\\Rightarrow -1-3\lt x+3x \Rightarrow -4\lt 4x \Rightarrow -1\lt x,故選\bbox[red,2pt]{(C)}$$
解:
一個階梯垂直高度為a,共20個,所以總高度為20a,故選(A)。
解:
$$令\cases{\angle BAJ'=\angle B'AJ= a\\ \angle BAB'=b},由於正10邊形每一內角為(10-2)\times 180^\circ \div 10=144^\circ\\,因此\angle B'AJ'=144^\circ \Rightarrow a+b=144^\circ\cdots(1);\\又 \angle AJI=\angle AJ'I'=144^\circ \Rightarrow \angle JAJ'+\angle AJJ' = 144^\circ \Rightarrow \angle JAJ'+180^\circ-144^\circ =144^\circ \\ \Rightarrow \angle JAJ'=108^\circ \Rightarrow 108^\circ+2a+b=360^\circ \Rightarrow 2a+b=252^\circ\cdots(2)\\ (2)-(1) \Rightarrow a=252^\circ -144^\circ = 108^\circ,故選\bbox[red,2pt]{(B)}$$
解:$$f(x)=2x^3-10x^2+20x =(ax+b)(x^2+10)+100 \Rightarrow \cases{f(0)=0=10b+100\\ f(1)=12=11(a+b)+100} \\ \Rightarrow \cases{b=-10 \\ 11(a+b)=-88 \Rightarrow a+b=-8} \Rightarrow a-10=-8 \Rightarrow a=2 \Rightarrow \cases{a=2\\b=-10} \\ \Rightarrow {b\over a}={-10\over 2}=-5,故選\bbox[red,2pt]{(B)}$$
解:
解:$$y=-2x^2+4x+6 =-2(x^2-2x)+6 =-2(x^2-2x+1)+2+6 =-2(x-1)^2+8\\ \Rightarrow y=-2(x-1)^2+8=a(x+h)^2+k \Rightarrow \cases{a=-2\\ h=-1\\ k=8} \Rightarrow a+h+k = -2-1+8=5\\,故選\bbox[red,2pt]{(A)}$$
解:$$(\sqrt 5-1)x=12 \Rightarrow x={12 \over \sqrt 5-1} ={12(\sqrt 5+1) \over (\sqrt 5-1)(\sqrt 5+1)} = {12(\sqrt 5+1) \over 4} =3(\sqrt 5+1)= 3\sqrt 5+3\\,故選\bbox[red,2pt]{(D)}$$
解:$$\cases{a=-3^4\\ b=(-3)^4 =3^4\\ c=(2^3)^4 =2^{12}\\ d=(2^2)^6=2^{12}} \Rightarrow \cases{a\ne b\\ c=d},故選\bbox[red,2pt]{(C)}$$
解:$$\cases{a=-3^4\\ b=(-3)^4 =3^4\\ c=(2^3)^4 =2^{12}\\ d=(2^2)^6=2^{12}} \Rightarrow \cases{a\ne b\\ c=d},故選\bbox[red,2pt]{(C)}$$
解:$$在第n頁寫出:\overbrace{n, n+1, n+2,..., 2n-1}^{n個數字}。\\由於要第1次出現1000,所以從最後一個數字,依次往前檢查:\\\cases{2n-1=1000 \Rightarrow n不是整數\\ 2n-2=1000 \Rightarrow n=501 \\ 2n-3=1000 \\\cdots} \Rightarrow 第1次出現1000在第501頁,故選\bbox[red, 2pt]{(B)}$$
解:$$\cases{(A)\angle B=37 \Rightarrow \angle C=180-27-37= 116 \gt 90\\ (B)\angle B=57 \Rightarrow \angle C=180-27-57= 96 \gt 90\\ (C)\angle B=77 \Rightarrow \angle C=180-27-77= 76 \lt 90\\ (D)\angle B=97 \gt 90}\\ \Rightarrow 當\angle B=77時,三內角分別為27,77,76,此為銳角三角形,故選\bbox[red,2pt]{(C)}$$
$$假設P為\overline{AC}與\overline{BD}的交點,由於ABCD為菱形,因此P為\overline{BD}的中點且\overline{AC}\bot \overline{BD},如上圖;\\ \overline{BP} =\overline{BD}\div 2=16\div 2=8 \Rightarrow \overline{AP}^2 = \overline{AB}^2-\overline{BP}^2 =17^2-8^2=225\\ 直角\triangle APE中,\overline{AE}^2 = \overline{AP}^2+(8+\overline{DE})^2 \Rightarrow 25^2=225+(8+\overline{DE})^2 \Rightarrow (8+\overline{DE})^2=400\\ \Rightarrow 8+\overline{DE}=20 \Rightarrow \overline{DE}=12,故選\bbox[red, 2pt]{(D)}$$
解:
上學期舞蹈社占全部的3/(3+4+5)=1/4,溜冰社占全部的1/3
下學期舞蹈社占全部的4/(4+3+2)=4/9,溜冰社占全部的1/3
1/4<4/9⇒舞蹈社增加,溜冰社不變,故選(D)。
解:$$假設\cases{甲袋取出的牌號為a\\ 乙袋取出的牌號為b},則(a,b)共有4\times 3=12種情形\\,其中(4,3),(4,4),(3,4),3種情形符合a+b \gt 6;因此機率為{3\over 12} ={1\over 4},故選\bbox[red, 2pt]{(C)}$$
上學期舞蹈社占全部的3/(3+4+5)=1/4,溜冰社占全部的1/3
下學期舞蹈社占全部的4/(4+3+2)=4/9,溜冰社占全部的1/3
1/4<4/9⇒舞蹈社增加,溜冰社不變,故選(D)。
解答:
$$G為重心\Rightarrow \triangle AGB ={1\over 3}\triangle ABC \Rightarrow \overline{AB}\times \overline{GD} ={1\over 3}\times \overline{AC}\times \overline{BC} \Rightarrow 29\times \overline{GD} ={1\over 3}\times 20\times 21\\ \Rightarrow \overline{GD}={140\over 29},故選\bbox[red,2pt]{(C)}$$
解:$$(250+0.9+0.8+0.7)^2 -(250-0.9-0.8-0.7)^2 =(250+2.4)^2 -(250-2.4)^2\\ =(250+2.4+250-2.4)(250+2.4-250+2.4) =500\times 4.8 = 2400,故選\bbox[red, 2pt]{(D)}$$
解:
解:
解:
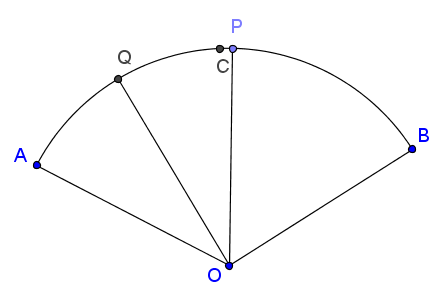
當P=C時,∠QOP=30
當P向右移2X度後,∠AOP=60+2X⇒∠QOP=∠AOP/2=30+X
所以P越往右移,∠QOP越大,扇形POQ面積越大
解:
解:
甲的作法:由於PE//AB且QR//FE,所以PQFE及PFER兩者皆為平行四邊形。因此PQ=FE,FE=PR,所以PQ=PR。
乙的作法:由於PE//AB,所以△RPE與△RAQ相似。因此RP:PQ=RE:EA=1:1,P為QR中點。
解:$$圓心在任一弦的中垂線上,即\overset{\Large{\frown}}{AD} =\overset{\Large{\frown}}{DC} =\angle B = 180^\circ-\angle A-\angle C=180^\circ-36^\circ- 60^\circ = 84^\circ\\ \angle BOD = \overset{\Large{\frown}}{DC} +\overset{\Large{\frown}}{CB} =84^\circ +2\times 36^\circ = 156^\circ,故選\bbox[red, 2pt]{(C)}$$
解:
$$E在\overline{AD}的中垂線上\Rightarrow \overline{EA}=\overline{ED} \Rightarrow \angle EAD=\angle EDA\\,又\overline{AD}為\angle A的角平分線,即\angle BAD=\angle EAD,因此 \angle EDA=\angle BAD \Rightarrow \overline{AB}\parallel \overline{DE} (內錯角相等)\\,故選\bbox[red, 2pt]{(B)}$$
解:$$(3x-c)^2-60=0 \Rightarrow 3x-c= \pm \sqrt{60} \Rightarrow x={c\pm \sqrt{60}\over 3} \gt 0\\ \Rightarrow c-\sqrt {60}\gt 0 \Rightarrow c\gt \sqrt{60} \Rightarrow c=8 ( 因為60\lt 8^2),故選\bbox[red, 2pt]{(B)}$$
全校的中位數(紅線位置)約在70分處,全校的Q3(藍線位置)約75分處
阿成的分數位在65百分位數,也就是介於50%~75%之間(紅藍線之間)。
以全班成績來看,阿成的分數超過全班的Q3。全班32人,Q3約占32/4=8人,所以選(A)。
解:
當P=C時,∠QOP=30
當P向右移2X度後,∠AOP=60+2X⇒∠QOP=∠AOP/2=30+X
所以P越往右移,∠QOP越大,扇形POQ面積越大
故選(A)。
$$\overline{AD} \parallel\overline{HE} \Rightarrow \angle DEH = \angle C = \angle A=60^\circ;\\作\overline{DP} \bot \overline{HE} \Rightarrow \angle PDE = 90^\circ-\angle DEH=90^\circ-60^\circ=30^\circ \Rightarrow \cases{\overline{PE}= {1\over 2}\overline{DE} =2 \\\overline{DP}={\sqrt 3\over 2}\overline{DE} =2\sqrt 3} \\ \Rightarrow \overline{HP}= \overline{HE}-\overline{PE}=5-2=3 \Rightarrow 梯形HEDI面積= 矩形DPHI+\triangle DPE \\= 3\times 2\sqrt 3+{1\over 2}\times 2\times 2\sqrt 3 =6\sqrt 3+2\sqrt 3=8\sqrt 3,故選\bbox[red, 2pt]{(B)}$$
解:$$AEFD \sim EBCF \Rightarrow {\overline{AE}\over \overline{EB}}={4\over 6} ={\overline{AD}\over \overline{EF}} ={\overline{EF}\over \overline{BC}} \Rightarrow \cases{\overline{AD}={4\over 6}\overline{EF} \\\overline{BC}={6\over 4}\overline{EF}} \Rightarrow {\overline{AD}\over \overline{BC}}= {4/6\over 6/4} ={16\over 36} ={4\over 9}\\,故選\bbox[red, 2pt]{(D)}$$
解:$$AEFD \sim EBCF \Rightarrow {\overline{AE}\over \overline{EB}}={4\over 6} ={\overline{AD}\over \overline{EF}} ={\overline{EF}\over \overline{BC}} \Rightarrow \cases{\overline{AD}={4\over 6}\overline{EF} \\\overline{BC}={6\over 4}\overline{EF}} \Rightarrow {\overline{AD}\over \overline{BC}}= {4/6\over 6/4} ={16\over 36} ={4\over 9}\\,故選\bbox[red, 2pt]{(D)}$$
甲的作法:由於PE//AB且QR//FE,所以PQFE及PFER兩者皆為平行四邊形。因此PQ=FE,FE=PR,所以PQ=PR。
乙的作法:由於PE//AB,所以△RPE與△RAQ相似。因此RP:PQ=RE:EA=1:1,P為QR中點。
甲、乙兩人作法皆正確,故選(A)。
--- END ---
解題僅供參考,其他基測試題及詳解--- END ---















































作者已經移除這則留言。
回覆刪除為何移除
刪除謝謝你在網路上提供資料,但對於33題有一個疑問
回覆刪除AD:BC=4:9
若假設
AD=2 與AD=20 ,其 AD:BC長度比還會是一樣4:9嗎?
我想BC大於AD的長度是固定的,當AD長度不同時,其比例也不同.
這一題應題目應該只告知一邊斜邊的長度,求另一邊的長度才比較合理.
三小
刪除第26答案沒用紅字標
回覆刪除這是比較早的貼文,每一題都沒有紅字標示,改天再來修訂!!謝謝!!
刪除第二題最後的答案應該是負二又12分之五,而不是負二又22分之五喔
回覆刪除