105年大學指考數學甲詳解

105學年度指定科目考試試題

數學甲

第壹部分：選擇題
一、單選題

解：$$\left( 1 \right) a=1\Rightarrow \log { 1 } -\log { x } =\log { \left( 1-x \right) } \Rightarrow \log { \frac { 1 }{ x } } =\log { \left( 1-x \right) } \Rightarrow \frac { 1 }{ x } =1-x\\ \Rightarrow x^{ 2 }-x+1=0\Rightarrow 判別式1-4=-3<0\Rightarrow 無實數解\\ (2)a=2\Rightarrow \log { 2 } -\log { x } =\log { \left( 2-x \right) } \Rightarrow \log { \frac { 2 }{ x } } =\log { \left( 2-x \right) } \Rightarrow \frac { 2 }{ x } =2-x\\ \Rightarrow x^{ 2 }-2x+2=0\Rightarrow 判別式4-8=-4<0\Rightarrow 無實數解\\ (3)a=3\Rightarrow \log { 3 } -\log { x } =\log { \left( 3-x \right) } \Rightarrow \log { \frac { 3 }{ x } } =\log { \left( 3-x \right) } \Rightarrow \frac { 3 }{ x } =3-x\\ \Rightarrow x^{ 2 }-3x+3=0\Rightarrow 判別式9-12=-3<0\Rightarrow 無實數解\\ \left( 4 \right) a=4\Rightarrow \log { 4 } -\log { x } =\log { \left( 4-x \right) } \Rightarrow \log { \frac { 4 }{ x } } =\log { \left( 4-x \right) } \Rightarrow \frac { 4 }{ x } =4-x\\ \Rightarrow x^{ 2 }-4x+4=0\Rightarrow { \left( x-2 \right) }^{ 2 }=0\Rightarrow 有一實數解\\ \left( 5 \right) a=5\Rightarrow \log { 5 } -\log { x } =\log { \left( 5-x \right) } \Rightarrow \log { \frac { 5 }{ x } } =\log { \left( 5-x \right) } \Rightarrow \frac { 5 }{ x } =5-x\\ \Rightarrow x^{ 2 }-5x+5=0\Rightarrow 判別式25-20=5>0\Rightarrow 有相異實數解$$

故選\(\bbox[red,2pt]{(5)}\)

---

解：

\(\cos{2.6\pi}=\cos{0.6\pi}=\cos{108^\circ}=\frac{x}{r}\)，見上圖。
由於\(r\approx y >> x\)，因此\(\frac{x}{r}\approx\frac{x}{y}=\cot{108^\circ}\)

故選\(\bbox[red,2pt]{(3)}\)

---

解：

$$\left( 1 \right) \cos { A } =\frac { 5^{ 2 }+6^{ 2 }-8^{ 2 } }{ 2\times 5\times 6 } =\frac { -1 }{ 20 } \Rightarrow \vec { AB } \cdot \vec { AC } =5\times 6\times \frac { -1 }{ 20 } =-\frac { 3 }{ 2 } \\ \left( 2 \right) \vec { AB } \cdot \vec { CA } =-\left( \vec { AB } \cdot \vec { AC } \right) =\frac { 3 }{ 2 } \\ \left( 3 \right) \cos { B } =\frac { 5^{ 2 }+8^{ 2 }-6^{ 2 } }{ 2\times 5\times 8 } =\frac { 53 }{ 80 } \Rightarrow \vec { AB } \cdot \vec { BC } =-\left( \vec { BA } \cdot \vec { BC } \right) =-5\times 8\times \frac { 53 }{ 80 } =-\frac { 53 }{ 2 } \\ \left( 4 \right) \vec { AB } \cdot \vec { CB } =-\left( \vec { AB } \cdot \vec { BC } \right) =\frac { 53 }{ 2 } \\ \left( 5 \right) \vec { AB } \cdot \vec { AB } =5\times 5=25$$

故選\(\bbox[red,2pt]{(4)}\)

---

解：
$$ax^{ 2 }+bx=ax+b\Rightarrow ax^{ 2 }+\left( b-a \right) x-b=0\Rightarrow 切點只有一個,判別式{ \left( a-b \right) }^{ 2 }+4ab=0\\ \Rightarrow { \left( a+b \right) }^{ 2 }=0\Rightarrow -a=b\Rightarrow ax^{ 2 }-2ax+a=0\Rightarrow a{ \left( x-1 \right) }^{ 2 }=0\\ \Rightarrow 切點位於x=1\Rightarrow 切點坐標為\left( 1,a+b \right) =\left( 1,0 \right) $$

故選\(\bbox[red,2pt]{(1)}\)

---

二、多選題

解：
(1)   平面E的法向量應為\(\vec{OP}=(2, 2, 1)\)
(2)   點(4,  4, 2)在直線\(\overline{OP}\)上，且點P是原點與點(4,4,2)的中點，所以點P也是E上距離(4,4,2)最近的點。
(3)   平面E的方程式為\(2(x-2)+2(y-2)+(z-1)=0\Rightarrow   2x+2y+z=9\)，點(0,0,9)符合該方程式，所以點(0,0,9)在平面E上
(4)   點(2,2,-8)至平面E的距離=\(\left|\frac{4+4-8-9}{\sqrt{2^2+2^2+1^2}}\right|=3\)
(5)   過原點與點(2,2,-8)的直線L，其向量為(2,2,-8)=2(1,1,-4)，因此L為\((t,t,-4t)\)；將L代入E可得   \( 2t+2t-4t-9=-9\ne   0\Rightarrow   L\)與平面不相交。

故選\(\bbox[red,2pt]{(2, 3)}\)

---

解：$$M=\begin{bmatrix} a & b \\ c & d \end{bmatrix}\Rightarrow \begin{cases} \begin{bmatrix} a & b \\ c & d \end{bmatrix}\begin{bmatrix} 3 \\ -2 \end{bmatrix}=\begin{bmatrix} 3 \\ 2 \end{bmatrix} \\ \begin{bmatrix} a & b \\ c & d \end{bmatrix}\begin{bmatrix} 3 \\ 2 \end{bmatrix}=-\begin{bmatrix} 3 \\ 2 \end{bmatrix} \end{cases}\Rightarrow \begin{cases} \begin{cases} 3a-2b=3 \\ 3c-2d=2 \end{cases} \\ \begin{cases} 3a+2b=-3 \\ 3c+2d=2 \end{cases} \end{cases}\Rightarrow M=\begin{bmatrix} 0 & -\frac { 3 }{ 2 } \\ \frac { 2 }{ 3 } & 0 \end{bmatrix}$$
(1) M不是鏡射變換
(2)   符合題意所述
(3)   $$\begin{cases} MC=\begin{bmatrix} 0 & -\frac { 3 }{ 2 }  \\ \frac { 2 }{ 3 }  & 0 \end{bmatrix}\begin{bmatrix} -3 \\ 2 \end{bmatrix}=\begin{bmatrix} -3 \\ -2 \end{bmatrix}=D \\ MD=\begin{bmatrix} 0 & -\frac { 3 }{ 2 }  \\ \frac { 2 }{ 3 }  & 0 \end{bmatrix}\begin{bmatrix} -3 \\ -2 \end{bmatrix}=\begin{bmatrix} 3 \\ -2 \end{bmatrix}=A \end{cases}$$
(4) $$\left| M \right| =\begin{vmatrix} 0 & -\frac { 3 }{ 2 }  \\ \frac { 2 }{ 3 }  & 0 \end{vmatrix}=1\neq -1$$
(5) $$M^{ 3 }=\begin{bmatrix} 0 & -\frac { 3 }{ 2 }  \\ \frac { 2 }{ 3 }  & 0 \end{bmatrix}\begin{bmatrix} 0 & -\frac { 3 }{ 2 }  \\ \frac { 2 }{ 3 }  & 0 \end{bmatrix}\begin{bmatrix} 0 & -\frac { 3 }{ 2 }  \\ \frac { 2 }{ 3 }  & 0 \end{bmatrix}=\begin{bmatrix} -1 & 0 \\ 0 & -1 \end{bmatrix}\begin{bmatrix} 0 & -\frac { 3 }{ 2 }  \\ \frac { 2 }{ 3 }  & 0 \end{bmatrix}=\begin{bmatrix} 0 & \frac { 3 }{ 2 }  \\ -\frac { 2 }{ 3 }  & 0 \end{bmatrix}=-M$$

故選\(\bbox[red,2pt]{(2, 3, 5)}\)

---

解：
令\(A、B\)在第\(n\)秒時的位置分別是\(a_n及b_n\)，則
\(a_n=1+\frac{1}{2}+{\frac{1}{2}}^2+\cdots+{\frac{1}{2}}^{n-1}=2-\frac{1}{2^{n-1}}\)
\(b_n=8-4-\frac{4}{3}-\frac{4}{3^2}-\cdots-\frac{4}{3^{n-1}}=8-4\left(1+\frac{1}{3}+\cdots+\frac{1}{3^{n-1}}\right)=2\left(1+\frac{1}{3^{n-1}}\right)\)
\(\Rightarrow c_n=\frac{1}{2}(a_n+b_n)=2+\frac{1}{3^{n-1}}-\frac{1}{2^n}\)
(1) \(c_1=2+1-\frac{1}{2}=\frac{5}{2}\)
(2)   \(c_2=2+\frac{1}{3}-\frac{1}{4}=\frac{25}{12}<c_1\)
(3)   \(c_{n+1}-c_n=2+\frac{1}{3^n}-\frac{1}{2^{n+1}}-(2+\frac{1}{3^{n-1}}-\frac{1}{2^n})  =\frac{1}{2^{n+1}}-\frac{2}{3^n}\)，不是等比數列
(4) \(\lim _{ n\rightarrow \infty  }{ c_{ n } } =\lim _{ n\rightarrow \infty  }{ \left\{ 2+\frac { 1 }{ 3^{ n-1 } } -\frac { 1 }{ 2^{ n } }  \right\}  } =2\)
(5)$$c_{ 1000 }=2+\frac { 1 }{ 3^{ 999 } } -\frac { 1 }{ 2^{ 1000 } } =2+\frac { 2^{ 1000 }-3^{ 999 } }{ 3^{ 999 }\times 2^{ 1000 } } \\ \log { 3^{ 999 } } =1000\log { 3 } -\log { 3 } =1000\times 0.4771-0.4771\approx 476.2\\ \log { 2^{ 1000 } } =1000\log { 2 } =1000\times 0.301=301\\ \Rightarrow \log { 3^{ 999 } } >\log { 2^{ 1000 } } \Rightarrow c_{ 1000 }<2$$
故選\(\bbox[red,2pt]{(1,4)}\)

---

三、選填題

解：
最初兩次的投擲中曾經出現過正面的情形為(正反)(反正)(正正)，機率為3/4；
最初兩次的投擲中曾經出現過正面且8次投擲恰好出現3次正面的情形：
正反+剩下6次中恰好出現2次正面→共\(\frac{6!}{4!}{2!}=15\)種情形
反正+剩下6次中恰好出現2次正面→共\(\frac{6!}{4!}{2!}=15\)種情形
正正+剩下6次中恰好出現1次正面→共6種情形
以上共有15+15+6=36種情形，機率為\(\frac{36}{2^8}\)，條件機率為\(\frac{\frac{36}{2^8}}{\frac{3}{4}}=\bbox[red,2pt]{\frac{3}{16}}\)

---

解：$$\vec { u } \times \vec { v } =\left( 1,2,3 \right) \times \left( 1,0,-1 \right) =\left( -2,4,-2 \right) \Rightarrow \vec { w } =\left( -2a,4a,-2a \right) \\ \begin{vmatrix} 1 & 2 & 3 \\ 1 & 0 & -1 \\ x & y & z \end{vmatrix}=-12\Rightarrow 3y-2x-2z+y=-12\Rightarrow -2x+4y-2z=-12\Rightarrow 4a+16a+4a=-12\\ \Rightarrow a=-\frac { 1 }{ 2 } \Rightarrow \vec { w } =\left( \bbox[red,2pt]{1,-2,1} \right) =\left( x,y,z \right) $$

---

解：
令\(z=a+bi\)，其中\(a,b\)皆為實數，則\(z-\bar{z}=-3i\Rightarrow (a+bi)-(a-bi)=-3i \Rightarrow b=-\frac{3}{2}\)
\(\left|\sqrt{7}+8i-z\right|=\left|\sqrt{7}+8i-a-bi\right|=\sqrt{{(a-\sqrt{7})}^2+(8+\frac{3}{2})^2}\Rightarrow a=\sqrt{7}有最小值8+\frac{3}{2}=\bbox[red,2pt]{\frac{19}{2}}\)

---

解：
這一類的題目只能列舉計算，總共有\(2^3=8\)種情形
(1,1,1):   機率=\(\frac{1}{4^3}\)，期望值=\(3\times\frac{1}{4^3}=\frac{3}{64}\)
(1,1,0):   機率=\(\frac{1}{4^2}\times\frac{3}{4}\)，期望值=\(2\times\frac{3}{4^3}=\frac{6}{64}\)
(1,0,1):   機率=\(\frac{1}{4}\times\frac{3}{4}\times\frac{3}{4}=\frac{9}{64}\)，期望值=\(2\times \frac{9}{64}=\frac{18}{64}\)
(1,0,0):   機率=\(\frac{1}{4}\times\frac{3}{4}\times\frac{1}{4}=\frac{3}{64}\)，期望值=\(1\times\frac{3}{64} =\frac{3}{64}\)
(0,1,1):   機率=\(\frac{3}{4}\times\frac{3}{4}\times\frac{1}{4}=\frac{9}{64}\)，期望值=\(2\times\frac{9}{64}=\frac{18}{64}\)
(0,1,0):   機率=\(\frac{3^3}{4^3}=\frac{27}{64}\)，期望值=\(1\times\frac{27}{64}=\frac{27}{64}\)

(0,0,1):   機率=\(\frac{3}{4}\times\frac{1}{4}\times\frac{3}{4}=\frac{9}{64}\)，期望值=\(1\times\frac{9}{64}=\frac{9}{64}\)

(0,0,0):  不用算，反正期望值=0

因此期望值=\(\frac{3}{64}+\frac{6}{64}+\frac{18}{64}+\frac{3}{64}+\frac{18}{64}+\frac{27}{64}+ \frac{9}{64}=\frac{84}{64}=\frac{21}{16}\)

答：\(\bbox[red,2pt]{\frac{21}{16}}\)

---

第二部份 非選擇題

解：

(1) \(\overline{BF}\)及\(\overline{BD}\)皆為切線，所以\(\overline{BD}=\overline{BF}=\bbox[red, 2pt]{x}\)；
\(\overline{CD}=\overline{BC}-\overline{BD}=\bbox[red,2pt]{4-x}\)；
\(\overline{CD}\)及\(\overline{CE}\)皆為切線，所以\(\overline{CE}=\overline{CD}=4-x \Rightarrow \overline{AE}=\overline{AC}+\overline{CE}=5+(4-x)=\bbox[red,2pt]{9-x}\)；
\(\overline{AE}\)及\(\overline{AF}\)皆為切線，所以\(\overline{AE}=\overline{AF}\)，也就是\( 9-x=6+x\Rightarrow \bbox[red,2pt]{x=\frac{3}{2}}\)

(2) \(\overline{BD}:\overline{CD}=\frac{3}{2}:4-\frac{3}{2}=3:5 \Rightarrow \vec{AD}=\frac{5}{8}\vec{AB}+\frac{3}{8}\vec{AC}\Rightarrow \bbox[red,2pt]{\alpha =\frac{5}{8}, \beta=\frac{3}{8}}\)

---

解：
(1) 由題意知 ：在\(0\le  x\le  3)\)範圍中，  f(0)=f(2)=12有最大值。若不考慮x範圍，一般的3次多項式只有一個極大值。因此x=0落在邊界上，而非斜率=0上。因此圖形為

由上圖可知: x 越大則f(x)越小，因此a<0；

(2)y=f(x)-12的圖形為上圖往下移12，即為下圖

由圖形可知, x=0, x=2為 f(x)-12=0的根，且x=0為二重根。因此\(f(x)-12=ax(x-2)^2 \Rightarrow f(x)=ax(x-2)^2+12\)。又$$\int _{ 0 }^{ x }{ f\left( t \right)  } dt=G\left( x \right) -G\left( 0 \right) \Rightarrow f\left( x \right) =G'\left( x \right) \Rightarrow G'\left( 1 \right) =0=f\left( 1 \right) \\ \Rightarrow a\times 1\times { \left( 1-2 \right)  }^{ 2 }+12=0\Rightarrow \bbox[red,2pt]{a=-12}$$
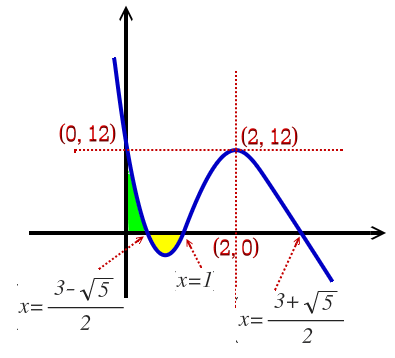
(3)$$G'\left( x \right) =f\left( x \right) =-12x{ \left( x-2 \right)  }^{ 2 }+12=-12\left[ x{ \left( x-2 \right)  }^{ 2 }-1 \right] =-12\left( x^{ 3 }-4x^{ 2 }+4x-1 \right) \\ =-12\left( x-1 \right) \left( x^{ 2 }-3x+1 \right) =-12\left( x-1 \right) \left( x-\frac { 3-\sqrt { 5 }  }{ 2 }  \right) \left( x-\frac { 3+\sqrt { 5 }  }{ 2 }  \right) $$

由f(x)=0的圖形及其根的相對位置如上圖；又\(\int _{ 0 }^{ x }{ f\left( t \right)  } dt\)其實就計算面積，面積最小值出現在x=0(G(0)=0,面積為0)或x=1時(黃色面積為負值、綠色面積為正值，若黃色面積>綠色面積，其值就比G(0)=0還小)；因此我們要確定G(0)與G(1)誰比較小？$$G\left( 1 \right) -G\left( 0 \right) =\int _{ 0 }^{ 1 }{ f\left( t \right)  } dt=\int _{ 0 }^{ 1 }{ \left( -12x^{ 3 }+48x^{ 2 }-48x+12 \right)  } dt\\ =\left. \left[ -3x^{ 4 }+16x^{ 3 }-24x^{ 2 }+12x \right]  \right| ^{ 1 }_{ 0 }=-3+16-24+12=1\\ \Rightarrow G\left( 1 \right) -G\left( 0 \right) =1\Rightarrow G\left( 1 \right) >G\left( 0 \right) $$因此當x=0，G(x)=0最小。

---

--  END  --