100年大學學測數學詳解

100 學年度學科能力測驗
數學科詳解

一、單選題

解：
取出黑球的機率為\(\frac{3}{5}\)、取出白球的機率為\(\frac{2}{5}\)，因此期望值為\(50\times   \frac{3}{5}+100\times\frac{2}{5}=30+40=70\)，故選\(\bbox[red,2pt]{(1)}\)

---

解：$$4\left( x^{ 2 }+1 \right) +{ \left( x+1 \right) }^{ 2 }\left( x-3 \right) +{ \left( x-1 \right) }^{ 3 }\\ =\left( 4x^{ 2 }+4 \right) +\left( x^{ 3 }-x^{ 2 }-5x-3 \right) +\left( x^{ 3 }-3x^{ 2 }+3x-1 \right) \\ =2x^{ 3 }-2x=2x(x^{ 2 }-1)=2x\left( x+1 \right) \left( x-1 \right) $$

故選\(\bbox[red,2pt]{(5)}\)

---

解：

$${ \left( a_{ n+1 } \right)  }^{ 2 }=\frac { 1 }{ \sqrt { 10 }  } { \left( a_{ n } \right)  }^{ 2 }\Rightarrow \log { { \left( a_{ n+1 } \right)  }^{ 2 } } =\log { \left( \frac { 1 }{ \sqrt { 10 }  } { \left( a_{ n } \right)  }^{ 2 } \right)  } \\ \Rightarrow 2\log { \left( a_{ n+1 } \right)  } =-\frac { 1 }{ 2 } +2\log { \left( a_{ n } \right)  } \Rightarrow \log { \left( a_{ n+1 } \right)  } -\log { \left( a_{ n } \right)  } =-\frac { 1 }{ 4 } \\ \Rightarrow b_{ n+1 }-b_{ n }=-\frac { 1 }{ 4 } \Rightarrow \left< b_{ n } \right> 為等差數列,公差為-\frac { 1 }{ 4 } $$
故選\(\bbox[red,2pt]{(2)}\)

---

解：

$$\left( \frac { { x }^{ 2 } }{ { 5 }^{ 2 } } +\frac { { y }^{ 2 } }{ { 4 }^{ 2 } }  \right) \left( \frac { { x }^{ 2 } }{ { 3 }^{ 2 } } -\frac { { y }^{ 2 } }{ { 4 }^{ 2 } }  \right) =0\Rightarrow \left( \frac { { x }^{ 2 } }{ { 5 }^{ 2 } } +\frac { { y }^{ 2 } }{ { 4 }^{ 2 } }  \right) \left( \frac { x }{ 3 } +\frac { y }{ 4 }  \right) \left( \frac { x }{ 3 } -\frac { y }{ 4 }  \right) =0\\ \Rightarrow \left( \frac { { x }^{ 2 } }{ { 5 }^{ 2 } } +\frac { { y }^{ 2 } }{ { 4 }^{ 2 } }  \right) =0或4x+3y=0或4x-3y=0$$

故選\(\bbox[red,2pt]{(3)}\)

---

解：$$\left( 1 \right) \times :\begin{cases} { \log { 3^{ 7 } } }=7\log { 3 } =7\times 0.4771\approx 3.34 \\ \log { 7^{ 3 } } =3\log { 7 } =3\times 0.8451\approx 2.54 \end{cases}\Rightarrow 3^{ 7 }>7^{ 3 }\\ \left( 2 \right) \times :\begin{cases} { \log { 5^{ 10 } } }=10\left( 1-\log { 2 } \right) =10\times 0.699\approx 7 \\ \log { 10^{ 5 } } =5 \end{cases}\Rightarrow 5^{ 10 }>10^{ 5 }\\ \left( 3 \right) \times :\begin{cases} { \log { 2^{ 100 } } }=10\log { 2 } =100\times 0.301=30.1 \\ \log { 10^{ 30 } } =30 \end{cases}\Rightarrow 2^{ 100 }>10^{ 30 }\\ \left( 4 \right) \times :\log _{ 2 }{ 3 } =\frac { \log { 3 } }{ \log { 2 } } =\frac { 0.4771 }{ 0.301 } \approx 1.59\\ \left( 5 \right) \bigcirc :{ 2 }^{ 3.5 }={ 2 }^{ 3 }\times { 2 }^{ 0.5 }=8\times \sqrt { 2 } =8\times 1.414\approx 11.3>11\Rightarrow { 2 }^{ 3.5 }>11\Rightarrow 3.5>\log _{ 2 }{ 11 } $$

故選\(\bbox[red,2pt]{(5)}\)

---

解：

將死亡率由小至大排列，第31個就是中位數；
超過0.2的死亡率由小至大排列為:   0.2019(25)、0.2034(26)、0.2051(27)、0.2085(28)、0.2123(29)、0.2137(30)、0.2164(31)、0.2166(32)....第31個為0.2164，故選\(\bbox[red,2pt]{(2)}\)

---

二、多選題

解：

(1)\(\bigcirc : \cos{60^\circ}=(\frac{1}{2},0)=D點\)
(2)\(\times  :\cos{50^\circ}+i\sin{50^\circ}=E(a,a)\)在線上，不在內部
(3)\(\bigcirc : \frac{4-3i}{5}=(\frac{4}{5},-\frac{3}{5}=F點\)
(4)\(\times: \frac{1+\sqrt{3}i}{2}=(\frac{1}{2},\frac{\sqrt{3}}{2}=G點\)，不在內部
(5)\(\bigcirc : (\cos{30^\circ}+i\sin{30^\circ})^{25}=(\cos{750^\circ}+i\sin{750^\circ})=(\cos{30^\circ}+i\sin{30^\circ})=(\frac{\sqrt{3}}{2},\frac{1}{2})=H點\)

故選\(\bbox[red,2pt]{(1,3,5)}\)

---

解：

$$\sin{\theta}=-\frac{2}{3}且\cos{\theta}>0\Rightarrow \cos{\theta}=\frac{\sqrt{5}}{3}\\
(1)\bigcirc:\tan{\theta}=\frac{\sin{\theta}}{\cos{\theta}}=\frac{負}{正}<0\\
(2)\bigcirc:\tan^2{\theta}=\left(\frac{\sin{\theta}}{\cos{\theta}}\right)^2=\left(\frac{-\frac{2}{3}}{\frac{\sqrt{5}}{3}}\right)^2=\left(\frac{2}{\sqrt{5}}\right)^2=\frac{4}{5}>\frac{4}{9}\\
(3)\times:\begin{cases} \sin ^{ 2 }{ \theta } ={ \left( -\frac { 2 }{ 3 } \right) }^{ 2 }=\frac { 4 }{ 9 } \\ \cos ^{ 2 }{ \theta } ={ \left( \frac { \sqrt { 5 } }{ 3 } \right) }^{ 2 }=\frac { 5 }{ 9 } \end{cases}\Rightarrow \cos ^{ 2 }{ \theta } >\sin ^{ 2 }{ \theta } \\
(4)\times:\sin{2\theta}=2\sin{\theta}\cos{\theta}=2\times\frac{-2}{5}\times\frac{\sqrt{5}}{5}<0\\
(5)\times:\cos{2\theta}=2\cos^2{\theta}-1=2\times\frac{5}{9}-1>0\Rightarrow (\sin{\theta},\cos{\theta})=(\sin{2\theta},\cos{2\theta})=(負,正)\\\Rightarrow \theta,2\theta在同象限$$

答：\(b=\bbox[red,2pt]{(1,2)}\)

---

解：

$$(1)\times:C_1半徑=\frac{1}{2}\times\overline{AB}=\frac{1}{2}\times 5=2.5\ne2\\(2)\times:C_1的圓心O_1=\left(\frac{3+0}{2},\frac{0+4}{2}\right)=\left(\frac{3}{2},2\right)\\ (3)\bigcirc:4\times\frac{3}{2}+3\times 2=6+6=12\\ (4)\bigcirc:C_2的圓心O_2在\angle AOB的角平分線上,即斜率=1的直線上\\(5)\times:理由同(4)$$

故選：\(\bbox[red,2pt]{(3,4)}\)

---

解：$$(1)\bigcirc :\vec { w } =(a,b)\Rightarrow \begin{cases} \vec { w } \cdot \vec { v } =0 \\ \left| \vec { w } \right| =\left| \vec { v } \right| \end{cases}\Rightarrow \begin{cases} 2a+\sqrt { 5 } b=0 \\ a^{ 2 }+b^{ 2 }=9 \end{cases}\Rightarrow (a,b)=\begin{cases} (\sqrt { 5 } ,-2) \\ (-\sqrt { 5 } ,2) \end{cases}\\ (2){ \bigcirc :\left| \vec { v } +\vec { w } \right| }^{ 2 }={ \left| \vec { v } \right| }^{ 2 }+2\vec { v } \cdot \vec { w } +{ \left| \vec { w } \right| }^{ 2 }={ \left| \vec { v } \right| }^{ 2 }-2\vec { v } \cdot \vec { w } +{ \left| \vec { w } \right| }^{ 2 }={ \left| \vec { v } -\vec { w } \right| }^{ 2 }\\ (3)\times :\cos { \theta } =\frac { \left( \vec { v } +\vec { w } \right) \cdot \vec { w } }{ \left| \vec { v } +\vec { w } \right| \left| \vec { w } \right| } =\frac { \vec { v } \cdot \vec { w } +{ \left| \vec { w } \right| }^{ 2 } }{ \left| \vec { v } +\vec { w } \right| \left| \vec { w } \right| } =\frac { 0+9 }{ \sqrt { { \left| \vec { v } \right| }^{ 2 }+{ \left| \vec { w } \right| }^{ 2 } } \times \left| \vec { w } \right| } \\ =\frac { 9 }{ \sqrt { 18 } \times 3 } =\frac { 1 }{ \sqrt { 2 } } \Rightarrow \theta =45°\\ (4)\times :{ \left| \vec { u } \right| }^{ 2 }={ \left| a\vec { v } +b\vec { w } \right| }^{ 2 }=a^{ 2 }|\vec { v } |^{ 2 }+2ab(\vec { v } \cdot \vec { w } )+b^{ 2 }|\vec { w } |^{ 2 }=9a^{ 2 }+0+9b^{ 2 }\\ \Rightarrow |\vec { u } |=3\sqrt { a^{ 2 }+b^{ 2 } } \\ (5)\bigcirc :(1,0)=c\vec { v } +d\vec { w } \Rightarrow \begin{cases} (1,0)=c(2,\sqrt { 5 } )+d(\sqrt { 5 } ,-2)=(2c+\sqrt { 5 } d,-2d+{ \sqrt { 5 } }c) \\ (1,0)=c(2,\sqrt { 5 } )+d(-\sqrt { 5 } ,2)=(2c-\sqrt { 5 } d,2d+{ \sqrt { 5 } }c) \end{cases}\\ \Rightarrow \begin{cases} \begin{cases} 2c+\sqrt { 5 } d=1 \\ -2d+{ \sqrt { 5 } }c=0 \end{cases} \\ \begin{cases} 2c-\sqrt { 5 } d=1 \\ 2d+{ \sqrt { 5 } }c=0 \end{cases} \end{cases}\Rightarrow \begin{cases} (c,d)=\left( \frac { 2 }{ 9 } ,\frac { \sqrt { 5 } }{ 9 } \right) \\ (c,d)=\left( \frac { 2 }{ 9 } ,\frac { -\sqrt { 5 } }{ 9 } \right) \end{cases}\Rightarrow c>0$$

故選：\(\bbox[red,2pt]{(1,2,5)}\)

---

解：

只有(4)及(5)的圖形將圓C完全包住，故選：\(\bbox[red,2pt]{(4,5)}\)

---

解：

(1)\(\bigcirc:\)原點與球心(1,2,3)的距離平方為\(1^2+2^2+3^2=14\)
(2)\(\times:\)A與球心的距離平方為\(0+2^2+3^2=13<14\Rightarrow\)A在球內
(3)\(\bigcirc:\)B與球心的距離平方為\(2^2+2^2+3^2=17>14\Rightarrow\)B在球外，球內一點與球外一點的連線與球面有相交
(4)\(\bigcirc:\vec{BA}=(2,0,0)\Rightarrow\)直線AB上的點可表示成(t, 0, 0)；當t=1時，(t,0,0)至(1,2,3)的距離最小，即A為直線AB上距球心最近的點
(5)\(\times:\)$$\begin{cases} xy平面\cap S \\ yz平面\cap S \\ xz平面\cap S \end{cases}=\begin{cases} (x-1)^{ 2 }+(y-2)^{ 2 }+(-3)^{ 2 }=14 \\ (-1)^{ 2 }+(y-2)^{ 2 }+(z-3)^{ 2 }=14 \\ (x-1)^{ 2 }+(-2)^{ 2 }+(z-3)^{ 2 }=14 \end{cases}\Rightarrow \begin{cases} (x-1)^{ 2 }+(y-2)^{ 2 }=5 \\ (y-2)^{ 2 }+(z-3)^{ 2 }=13 \\ (x-1)^{ 2 }+(z-3)^{ 2 }=10 \end{cases}\\\Rightarrow \begin{cases} 半徑為\sqrt { 5 } 的圓 \\ 半徑為\sqrt { 13 } 的圓 \\ 半徑為\sqrt { 10 } 的圓 \end{cases}\Rightarrow S與yz平面所截的圓面積最大$$故選\(\bbox[red,2pt]{(1,3,4)}\)

---

解：$$\left( 1 \right) \times { : }f\left( \frac { 1 }{ \sqrt { 2 }  }  \right) =正\times 負\times 正<0\\ (2)\times { : }f\left( x \right) =2\Rightarrow x(x-1)(x+1)=2\Rightarrow x^{ 3 }-x-2=0\\ 若有整數解,其解為x=\pm 1,\pm 2,但將其代入皆不合\\ (3)\bigcirc :令g\left( x \right) =f\left( x \right) -(x^{ 2 }+1)=x^{ 3 }-x^{ 2 }-x-1\Rightarrow \begin{cases} g\left( 2 \right) =8-4-2-1=1>0 \\ g\left( 1 \right) =1-1-1-1=-2<0 \end{cases}\\ \Rightarrow g\left( x \right) =0有實數解介於1與2之間\\ (4)\times :f\left( x \right) =x\Rightarrow x^{ { 3 } }-2x=0\Rightarrow x=0,\pm \sqrt { 2 } \\ (5)\times { : }令g\left( x \right) =f\left( x \right) -2=x^{ 3 }-x-2,則\\ g\left( a \right) =0\Rightarrow a^{ 3 }-a-2=0\Rightarrow -a^{ 3 }+a-2=-4\Rightarrow g\left( -a \right) =-4\Rightarrow f\left( -a \right) =-2\neq 0$$

故選\(\bbox[red,2pt]{(3)}\)

---

第貳部份：選填題

解：$$\left\{ \begin{array}{ll} \frac { a }{ 1-r } =5 \\ \frac { a }{ 1-3r } =7 \end{array} \right. \Rightarrow \left\{ \begin{array}{ll} a=\frac { 35 }{ 8 }  \\ r=\frac { 1 }{ 8 }  \end{array} \right. \Rightarrow \frac { a }{ 1-2r } =\frac { \frac { 35 }{ 8 }  }{ 1-\frac { 2 }{ 8 }  } =\bbox[red,2pt]{\frac { 35 }{ 6 }} $$

---

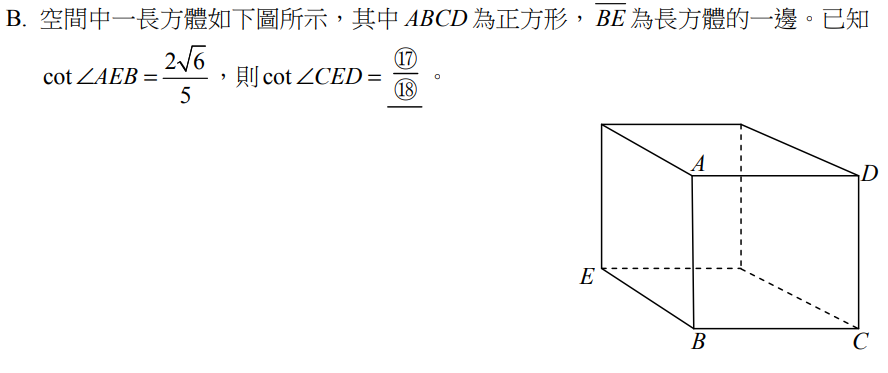
解：

$$\cot { \angle AEB } =\frac { 2\sqrt { 6 }  }{ 5 } =\frac { \overline { EB }  }{ \overline { AB }  } \Rightarrow \begin{cases} \overline { EB } =2\sqrt { 6 } a \\ \overline { AB } =5a \end{cases}\Rightarrow { \overline { CE }  }^{ 2 }={ \overline { EB }  }^{ 2 }+{ \overline { BC }  }^{ 2 }=24{ a }^{ 2 }+25{ a }^{ 2 }\\ \Rightarrow \overline { CE } =\sqrt { 24{ a }^{ 2 }+25{ a }^{ 2 } } =7a\Rightarrow \cot { \angle CED } =\frac { \overline { CE }  }{ \overline { CD }  } =\frac { 7a }{ 5a } =\bbox[red,2pt]{\frac { 7 }{ 5 } } $$

---

解：

1男2女+2男1女=\(\frac{C^{20}_{1}C^{15}_{2}+C^{20}_{2}C^{15}_{1}} {C^{35}_{3}}=\frac{2100+2850}{6545}=\frac{4950}{6545}=\frac{990}{1309}=\bbox[red,2pt]{\frac{90}{119}}\)

---

解：

$$\angle A=\angle C=90^{ \circ  }\Rightarrow \angle B+\angle D=180^{ \circ  }\Rightarrow \cos { \angle B } =-\cos { \angle D } \\ \Rightarrow \frac { 1+25-{ \overline { AC }  }^{ 2 } }{ 2\times 5\times 1 } =-\frac { 49+25-{ \overline { AC }  }^{ 2 } }{ 2\times 5\times 7 } \Rightarrow \frac { 26-{ \overline { AC }  }^{ 2 } }{ 10 } =-\frac { 74-{ \overline { AC }  }^{ 2 } }{ 70 } \\ \Rightarrow 182-7{ \overline { AC }  }^{ 2 }=-74+{ \overline { AC }  }^{ 2 }\Rightarrow 256=8{ \overline { AC }  }^{ 2 }\Rightarrow \overline { AC } =\bbox[red,2pt]{\sqrt { 32 }} $$

---

解：
假設目前(A、B、C)的質量分別為(a、b、c)公克，則半年前的質量分別為(2a,3b,4c)公克、一年前的質量分別為(4a,9b,16c)公克；由三種不同時間的輻射強度可得以下聯立方程式:$$\begin{cases} a+2b+c=8 \\ 2a+6b+4c=22 \\ 4a+18b+16c=66 \end{cases}\Leftrightarrow \begin{cases} a+2b+c=8 \\ a+3b+2c=11 \\ 2a+9b+8c=33 \end{cases}\Rightarrow \begin{cases} b+c=3 \\ 5b+6c=17 \end{cases}\Rightarrow \begin{cases} b=1 \\ c=2 \end{cases}\Rightarrow \begin{cases} a=4 \\ b=1 \\ c=2 \end{cases}$$

答：A、B、C的質量分別為\(\bbox[red,2pt]{4、1、2}\)公克

---

解：
E1: 焦點在(3,0)及(-3,0)，則\(a^2=b^2+3^2\Rightarrow b^2=a^2-9\)，即\(E_1:\frac{x^2}{a^2}+\frac{y^2}{a^2-9}=1\)
E2: 拋物線方程式為\(y^2=12x\)
x=3代入E2，可得交點為(3,6)及(3,-6)；再將兩交點代入E1可得$$\frac { 3^{ 2 } }{ a^{ 2 } } +\frac { 6^{ 2 } }{ a^{ 2 }-9 } =1\Rightarrow \frac { 36 }{ a^{ 2 }-9 } =\frac { a^{ 2 }-9 }{ a^{ 2 } } \Rightarrow a^{ 2 }-9=6a(\because a>0,\therefore -6a不合)\\ \Rightarrow a=\frac { 6+6\sqrt { 2 }  }{ 2 } (\because a>0,\therefore \frac { 6-6\sqrt { 2 }  }{ 2 } 不合)=\bbox[red,2pt]{3+3\sqrt { 2 }} $$另一種方法: E1及E2的交點(3,6)在橢圓上，則交點至兩焦點的和為2a，即\(\overline{(3,6),(3,0)}+\overline{(3,6),(-3,0)}=2a\Rightarrow 6+\sqrt{72}=2a\Rightarrow a=3+3\sqrt{2}\)

---

解：
平面H的法向量\(\vec{u}=(1,-1,1), \vec{OP}=(2,1,1)\)，則L的方向向量\(=\vec{u}\times\vec{OP} =(1,-1,1)\times (2,1,1) = (-2,1,3)=\bbox[red,2pt]{(2,-1,-3)}\)

---