109年新北市立高中教甄聯招-數學科詳解

新北市立高級中等學校109學年度教師聯合甄選數學科試題

一、填充題： 70%，每題 7 分

解：

$$假設\cases{R:紅燈\\ X:非紅燈} \Rightarrow \cases{R\to X:機率為1\\ X\to R: 機率1/4\\ X\to X: 機率3/4}\\ R\to X \to R\to X \to X \to R\Rightarrow 機率=1\times {1\over 4}\times 1\times {3\over 4} \times {1\over 4}={3 \over 64} \\ R\to X \to X \to R \to X \to R\Rightarrow 機率=1\times {3\over 4}\times {1\over 4}\times 1 \times {1\over 4}={3 \over 64} \\ R\to X \to X \to X \to X \to R\Rightarrow 機率=1\times {3\over 4}\times {3\over 4}\times {3\over 4} \times {1\over 4}={27 \over 64} \\ \Rightarrow 機率為{3 \over 64}+{3 \over 64}+ {27 \over 256} = \bbox[red, 2pt]{51 \over 256}$$

---

解：

$$令\cases{\#(B)=B集合元素個數\\ \#(C)=C集合元素個數}，若\#(B)=k, 0 \le k \le 102, 則\#(C)=102-k, 102-k+1,...,102\\ 因此(B, C)共有 \sum_{n=0}^{102} C^{102}_n(C^n_0 + C^n_1 +\dots C^n_n) = \sum_{n=0}^{102} C^{102}_n\cdot 2^n = (2+1)^{102}= \bbox[red, 2pt]{3^{102}}$$

---

3. 一模型公司在一個內部邊長為 2 單位的透明正立方體箱子內放置一顆半徑為 1 單位的黃球，然後又在箱子的八個角落再塞入 8 顆半徑相同的小紅球，如下圖所示：

試求：小紅球的最大半徑為 單位。

解：

$$正立方體的對角線長為2\sqrt 3，扣除球直徑2，剩下2\sqrt 3-2\\，即單邊剩下空間對角線長為{2\sqrt 3-2 \over 2}=\sqrt 3-1;令小球半徑r\\ \Rightarrow \sqrt 3-1 = r+r\sqrt 3 \Rightarrow r={\sqrt 3-1 \over \sqrt 3+1} \Rightarrow {4-2\sqrt 3\over 2} =\bbox[red, 2pt]{2-\sqrt 3}$$

---

解：

$$\cases{\log a^{20}= 30+p_1,0\le p_1 < 1\\ \log ({1\over b})^{20} = -25+p_2, 0\le p_2 < 1 } \Rightarrow \cases{20\log a=30+p_1 \\ -20\log b=-25+p_2} \\\Rightarrow \cases{5\log a=30/4 + p_1/4 \\ 20\log b=25-p_2 = 24+p_3,0\le p_3< 1} \Rightarrow \cases{5\log a= 30/4+p_1/4\\ 5\log b=24/4+p_3/4} \\ \Rightarrow 5(\log a+\log b) =\log (ab)^5 =13 +{1\over 2}+{p_1+p_3\over 4};\\由於0< {1\over 2}+{p_1+p_3\over 4}< 1 \Rightarrow (ab)^5是13+1=\bbox[red, 2pt]{14}位數$$

---

解：

$$此題相當於求x+y+z=10的整數解，需滿足條件:x\ge 1,y\ge 2,z\ge 3\\ \begin{array}{} x& y & z \\\hline 1 & 2 & 7\\ & 3 & 6 \\ & 4& 5 \\ &5 & 4\\ & 6& 3\\\hdashline 2& 2 & 6\\ & 3& 5\\ & 4 & 4\\ & 5& 3\\\hdashline 3 & 2 & 5\\ & 3& 4 \\& 4 & 3\\\hdashline 4 & 2 & 4\\ & 3 & 3\\\hdashline 5 & 2 & 3\\\hline\end{array} \Rightarrow 共有\bbox[red, 2pt]{15}種裝法$$

---

解：

$$令\angle P_1OQ_2 = \theta \Rightarrow \cases{h_1=\sin \theta \\ h_2=\sin(\theta+45^\circ)} \Rightarrow h_1+h_2 = \sin \theta + \sin(\theta+45^\circ) \\= \sin\theta + {\sqrt 2\over 2}(\sin \theta +\cos \theta)  ={\sqrt 2\over 2}\cos \theta +{2+\sqrt 2\over 2} \sin \theta \equiv a\cos \theta + b\sin \theta \\ \Rightarrow 最大值為\sqrt {a^2+ b^2} =\sqrt{{2\over 4} +{6+4\sqrt 2\over 4}} =\sqrt {2+\sqrt 2} \\ \Rightarrow \triangle P_1OQ_1 + \triangle P_2OQ_2 最大值為\bbox[red, 2pt]{{1\over 2}\sqrt {2+\sqrt 2} }$$

---

解：

$$\angle BAC=60^\circ \Rightarrow \angle COB=120^\circ \Rightarrow \angle COD=60^\circ  \Rightarrow \cases{\overline{DO}=1/2 \\ \overline{CD}=\sqrt 3/2} \Rightarrow \cases{A(1,0)\\ B(-1/2,-\sqrt 3/2) \\ C(-1/2,\sqrt 3/2) \\ P(3,0)} \\ \Rightarrow \cases{\overline{PA}=2 \\ \overline{PB}=\sqrt{ 49/4+3/4}= \sqrt{13} \\ \overline{PC}= \overline{PB} = \sqrt{13}} \Rightarrow \overline{PA}^2+ \overline{PB}^2+ \overline{PC}^2=4+13 + 13= \bbox[red, 2pt]{30}$$

---

解：

$$(1+x^5+x^7+x^{12})^{20} = (1+x^5+x^7(1+x^5))^{20} = (1+x^5)^{20}(1+x^7)^{20}\\ \Rightarrow x^{17}= (x^{5})^2 \times x^{7} \Rightarrow  係數為C^{20}_2C^{20}_1= 190\times 20 = \bbox[red, 2pt]{3800}$$

---

解：

$$註:\cases{2^k \cdot (-1)^k =(-2)^k \\ (-2)^k \cdot (-2)^k = (-2)^{2k}=2^{2k}}\\ (2^{k+1}+(-1)^{k+1})(2^k+(-1)^k) = 2^{2k+1}+2\cdot (-2)^k-(-2)^k+(-1)^{2k+1}) = 2^{2k+1}+(-2)^k-1 \\ \Rightarrow {(-2)^k \over (2^{k+1}+(-1)^{k+1})(2^k+(-1)^k)} ={(-2)^k \over 2^{2k+1}+(-2)^k-1} = {(-2)^k \over 2\cdot( (-2)^k)^2+(-2)^k-1} \equiv {u \over 2u^2+u-1},其中u=(-2)^k \\ 又{u \over 2u^2+u-1} = { u \over (u+1)(2u-1)}={1\over 3}\left({1\over u+1} -{1\over 2u-1} \right) \equiv {1\over 3}\left({1\over (-2)^k+1} - {1\over 2(-2)^k-1} \right)\\ \Rightarrow  原式 = {1\over 3}\sum_{k=0}^\infty \left( {1\over (-2)^k+1} - {1\over 2(-2)^k-1}  \right)={1\over 3}\times {1\over 2} =\bbox[red,2pt]{1\over 6}$$ (待續...)

---

解：

$$若x^2+y^2-2x+4y-18 \ge 0 \Rightarrow |x^2+y^2-2x+4y-18|=x^2+y^2-2x+4y-18 \le 2x-2y+18 \\ \qquad\Rightarrow x^2-4x+y^2+6y-36 \le 0  \Rightarrow (x-2)^2 +(y+3)^2 \le 7^2\Rightarrow 藍色區域 \\若x^2+y^2-2x+4y-18 < 0 \Rightarrow |x^2+y^2-2x+4y-18|= -x^2-y^2+2x-4y+18 \le 2x-2y+18\\ \qquad \Rightarrow x^2+y^2+2y \ge 0 \Rightarrow x^2+(y+1)^2 \ge 1^2 \Rightarrow 橘色區域\\ 藍色+橘色區域面積=7^2\pi -1^2\pi = \bbox[red, 2pt]{48\pi}$$

---

解：

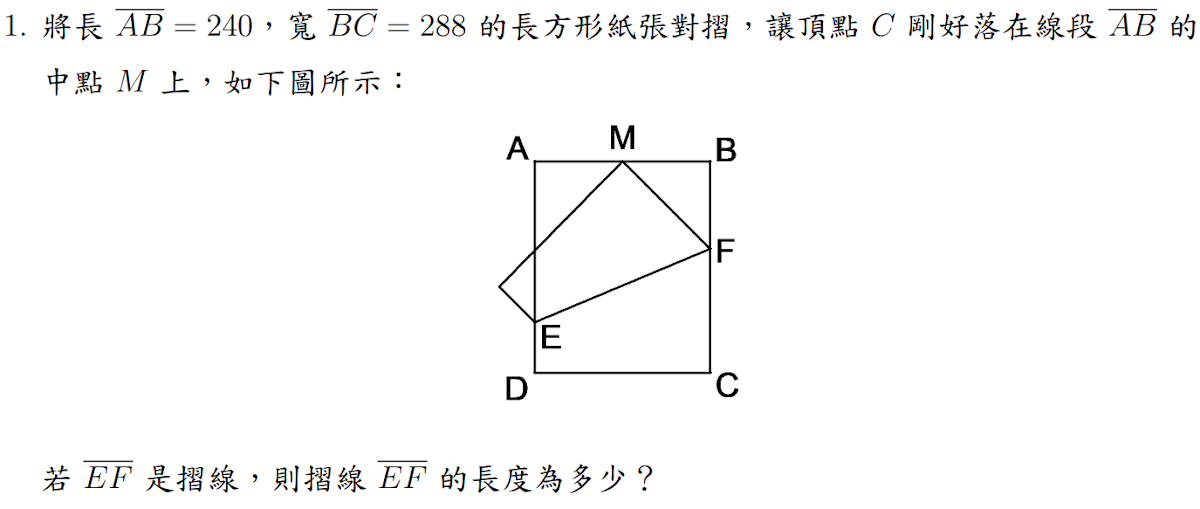
$$令\overline{MF} =\overline{FC}=a \Rightarrow 在直角\triangle BMF中，\overline{MF}^2 = \overline{MB}^2 + \overline{BF}^2 \Rightarrow a^2=120^2+(288-a)^2 \Rightarrow a=169\\ 令\overline{DE}= \overline{EG} =b \Rightarrow \overline{AE}=288-b \Rightarrow \cases{直角\triangle MAE: \overline{ME}^2 = \overline{MA}^2 + \overline{AE}^2 =120^2+(288-b)^2 \\ 直角\triangle EDC: \overline{EC}^2 = \overline{ED}^2 + \overline{DC}^2 =b^2+240^2}\\ 由於\overline{EM} =\overline{EC} \Rightarrow 120^2+(288-b)^2 =b^2+240^2 \Rightarrow b=69 \\ 直角\triangle FHE: \overline{EF}^2= \overline{EH}^2 + \overline{HF}^2 =240^2+ (a-b)^2=240^2+ (169-69)^2=260^2 \Rightarrow \overline{EF} =\bbox[red, 2pt]{260}$$

---

解：

(a) $$\cases{\overline{OA}= \sqrt{5^2+3^2 +4^2} =5\sqrt 2 \\ \text{dist}(A,E)={5-8+6\over \sqrt{1^2+2^2+2^2}}= 1}, 令A在E的投影點為B\Rightarrow \text{dist}(A,E)=\overline{AB} \\直角\triangle ABO: \overline{AO}^2 = \overline{AB}^2 + \overline{OB}^2 \Rightarrow 50=1+ \overline{OB}^2 \Rightarrow \overline{OB}=7;\\ 假設\overline{BP}=r \Rightarrow {\overline{OP} \over \overline{AP}}=f(r)={7+r\over \sqrt{1+r^2}} \Rightarrow f'(r)={-7r+1\over (1+r^2)^{3/2}} =0 \Rightarrow r={1 \over 7} \\ \Rightarrow 最大值為f({1\over 7})={50/7\over \sqrt{50/49}} =\bbox[red,2pt]{\sqrt{50}}$$ (b) $$平面E的法向量\vec n=(1,2,2)即為\overleftrightarrow{AB}方向向量 \Rightarrow 直線\overline{AB}的方程式{x-5\over 1} ={y+4 \over 2} ={z-3\over 2} \\ \Rightarrow 直線\overline{AB}上的點可表示成(t+5,2t-4,2t+3), 由\overline{AB}=1 \Rightarrow t^2+4t^2+4t^2 = 1 \Rightarrow 9t^2=1 \\\Rightarrow t=\pm 1/3 \Rightarrow B=\cases{(16/3,-10/3,11/3),t=1/3\\ (14/3,-14/3,7/3),t=-1/3}, 由於(16/3,-10/3,11/3) 不在E上\\，因此B={(14/3,-14/3,7/3)} \Rightarrow \overleftrightarrow{OB}:{x\over 2}={y\over -2}=z \Rightarrow P(2s,-2s,s), s\in \mathbb R \\ 又\overline{OP}=7+r=7+{1\over 7}={50\over 7} = \sqrt{4s^2+4s^2+s^2} \Rightarrow s={50\over 21} \Rightarrow P=\bbox[red, 2pt]{({100\over 21}, -{100\over 21}, {50\over 21} )}$$

---

-- END   (僅供參考)  --