教育部受託辦理106學年度
公立高級中等學校教師甄選
數學科試題
公立高級中等學校教師甄選
數學科試題
第一部分:選擇題
一、單選題
解:
$$a=\sqrt[3]{3-\sqrt 5\over 2} +\sqrt[3]{3+\sqrt 5\over 2} \Rightarrow a^3={3-\sqrt 5\over 2}+{3+\sqrt 5\over 2} +3\sqrt[3]{4\over 4}(\sqrt[3]{3-\sqrt 5\over 2} +\sqrt[3]{3+\sqrt 5\over 2})=3+3a \\ \Rightarrow a^3=3a+3 \Rightarrow \cases{a^6=(3a+3)^2=9a^2+18a+9\\ a^4=a(3a+3)=3a^2+3a} \\ \Rightarrow a^6-6a^4+9a^2+27 = 9a^2+18a+9-18a^2-18a+9a^2+27=36,故選\bbox[red, 2pt]{(B)}$$
$$\left(({4\over \sin^3 \theta})^2 +({1\over \cos^3 \theta})^2 \right)\left( \sin^2 \theta + \cos^2\theta \right)\ge \left( {4\over \sin^2\theta} +{1\over \cos^2 \theta} \right)^2 \\\Rightarrow \left({16\over \sin^6 \theta} +{1\over \cos^6 \theta} \right) \ge \left( {4\over \sin^2\theta} +{1\over \cos^2 \theta} \right)^2\cdots(1)\\ 又\left(({2\over \sin \theta})^2 +({1\over \cos \theta})^2 \right)\left( \sin^2 \theta + \cos^2\theta \right)\ge \left( 2+1 \right)^2 \Rightarrow \left( {4\over \sin^2\theta} +{1\over \cos^2 \theta} \right) \ge 9\cdots (2)\\ 由(1)及(2)可知 \left({16\over \sin^6 \theta} +{1\over \cos^6 \theta} \right) \ge 9^2=81,現在由題意知 \left({16\over \sin^6 \theta} +{1\over \cos^6 \theta} \right)=81\\,即柯西不等式的等號成立 \\ 也就代表{4\over \sin^4\theta} ={1\over \cos^4 \theta} \Rightarrow \tan^4 \theta=4 \Rightarrow \tan \theta=\sqrt 2(\theta為銳角,負值不合),故選\bbox[red, 2pt]{(D)}$$
解:
$$ab=4 \Rightarrow a={4\over b} \Rightarrow (\log_2 a)(\log_2 b)=(\log_2 {4\over b})(\log_2 b) = (2-\log_2 b)(\log_2 b)=-1\\ \Rightarrow (\log_2 b)^2-2(\log_2 b)-1=0 \Rightarrow \log_2 b={2\pm \sqrt{8}\over 2} = 1\pm \sqrt 2 ;\\同理,b={4\over a} \Rightarrow (\log_2 a)(\log_2 b)=(\log_2 a)(\log_2 {4\over a}) = (2-\log_2 a)(\log_2 a)=-1 \\ \Rightarrow (\log_2 a)^2-2(\log_2 a)-1=0 \Rightarrow \log_2 a={2\pm \sqrt{8}\over 2} = 1\pm \sqrt 2; \\ 由於 a> b> 0 \Rightarrow (\log_2 a,\log_2 b)=(1+\sqrt 2,1-\sqrt 2) \Rightarrow \log_a b = {\log_2 b \over \log_2 a} \\={1-\sqrt 2\over 1+\sqrt 2} = (1-\sqrt 2)(\sqrt 2-1)= -3+2\sqrt 2,故選\bbox[red, 2pt]{( A)}$$
解:
$${1\over x}+{1\over y}= {x+y \over xy}={1\over 1899} \Rightarrow xy-1899x-1899y=0 \Rightarrow (x-1899)(y-1899)=1899^2;\\ 由於1899^2 = 3^4\times 211^2 \Rightarrow 1899^2 有(4+1)(2+1)=15個正因數 \Rightarrow 有15組解,故選\bbox[red, 2pt]{(C )}$$
解:
$$\cases{A(-1,0)\\ B(1,0)\\ P(t,4-t)} \Rightarrow \cases{\overrightarrow{AP} =(t+1,4-t)\\ \overrightarrow{BP} =(t-1,4-t)} \Rightarrow \overrightarrow{AP} +\overrightarrow{BP} =(2t,8-2t) \\ \Rightarrow |\overrightarrow{AP} +\overrightarrow{BP}| =\sqrt{4t^2 +(8-2t)^2} =\sqrt{8(t-2)^2 +32} \Rightarrow 最小值為\sqrt{32} =4\sqrt 2,故選\bbox[red, 2pt]{(B )}$$
解:
$$8x-5y=37 \Rightarrow y={8x-37\over 5}\in N \Rightarrow x的個位數必須是4或9\\ \Rightarrow 106\le {8x-37\over 5}\le 2017 \Rightarrow 567 \le 8x \le 10122 \Rightarrow 71\le x \le 1265;\\由於題目限定106\le x \le 2017,因此106\le x \le 1265 \\ \Rightarrow x=109,114,119,124,\dots,1264,相當於等差數列\cases{a_1=109\\ d=5\\ a_n=1264}\\ \Rightarrow 1264=109+5(n-1) \Rightarrow n=231,因此共有232項,故選\bbox[red, 2pt]{(A )}$$
解:
$$\sum_{k=n}^{2n-1} {3\over \sqrt {nk}} ={3\over \sqrt {n^2}} +{3\over \sqrt {n^2+n}} +{3\over \sqrt {n^2+2n}} +\cdots +{3\over \sqrt {n^2+(n-1)n}} = \sum_{k=1}^{n} {3\over \sqrt {n^2-n+kn}} \\ ={1\over n}\sum_{k=1}^{n} {3\over \sqrt {1+{k-1\over n}}} \Rightarrow \lim_{n\to \infty}\left(\sum_{k=n}^{2n-1} {3\over \sqrt {nk}}\right) =\lim_{n\to \infty}\left( {1\over n}\sum_{k=1}^{n} {3\over \sqrt {1+{k-1\over n}}}\right)\\ =\int_0^1 {3\over \sqrt{1+x}}\;dx = \left. \left[ 6\sqrt{1+x}\right] \right|_0^1 =6(\sqrt 2-1) \approx 6(1.414-1)=6\times 0.414=2.484,故選\bbox[red, 2pt]{( D)}$$
解:
$$\cases{W:白球數6\\ R:紅球數2\\ G:綠球數2\\ B:黑球數2} \\\Rightarrow 白球先取完的機率:{R\over W+R} +{G\over W+G}+{B\over W+B}- {R+G\over W+R+G}- {G+B\over W+G+B}\\\qquad - {R+B\over W+R+B}+{R+G+B\over W+R+G+B}\\ ={2\over 8} +{2\over 8} +{2\over 8} -{4\over 10} -{4\over 10}-{4\over 10}+{6\over 12}={3\over 4}-{6\over 5}+{1\over 2}={1\over 20},故選\bbox[red, 2pt]{(B )}\\公式來源可參考\href{https://math.ntnu.edu.tw/~horng/letter/hpm17010.pdf}{按這裡}$$
二、複選題
$$9=\cases{3^2 = 3^{\log_2 4}\\ 2^{\log_2 9} = 2^{2\log_2 3} =4^{\log_2 3} }=a^{\log_b c} \Rightarrow (a,b,c)=(3,2,4) 或 (4,2,3) \\ \Rightarrow a^2+bc=\cases{9+8 =17\\ 16+6=22},故選\bbox[red, 2pt]{( AD)}$$
$$\bar X= (1+2 +2+3 +2)\div 5=2 \Rightarrow \cases{\sigma_X =\sqrt{1+0+0+1+0\over 5} =\sqrt{0.4} \\S_{XX}=\sum (x_i-\bar X)^2= 1+0+0+1=2 \\\bar Y={1\over 2}\bar X + 3=1+3=4}\\ \Rightarrow S_{XY}= \sum (x_i-\bar X)(y_i-\bar Y)=(-1)\cdot (-1)+ 0 + 0+1\cdot (a-4)+ 0=a-3\\ \Rightarrow 迴歸直線斜率={1\over 2} ={S_{XY}\over S_{XX}} ={a-3\over 2} \Rightarrow a=4 \Rightarrow \bar Y=4=(3+2+1+a+b)\div 5 \Rightarrow b=10\\(A)\bigcirc: b=10 >5 \\(B)\bigcirc: \cases{a=4\\ b=10} \Rightarrow a< b\\(C)\times: \sigma_Y=\sqrt{1+4+9+0+36\over 5}=\sqrt{10} \Rightarrow |\sigma_Y-\sigma_X| =|\sqrt{10}-\sqrt{0.4}| \not \gt 5\\(D)\times: r={S_{XY}\over \sqrt{S_{XX}S_{YY}}} ={1\over \sqrt{2\times 50}}=0.1 \ne 0.3,故選\bbox[red, 2pt]{( AB)}$$
解:
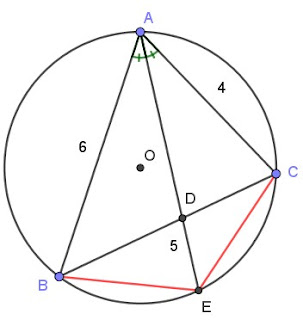
$$\overline{AD}為角平分線 \Rightarrow {\overline{AB}\over \overline{AC}} ={\overline{BD}\over \overline{DC}} \Rightarrow {6\over 4} ={\overline{BD}\over 5-\overline{BD}} \Rightarrow \overline{BD}=3\Rightarrow \overline{DC}=2\\ 餘弦定理: \cases{\cos \angle DAB = {\overline{AB}^2 +\overline{AD}^2-\overline{BD}^2 \over 2\times \overline{AB}\times \overline{AD}}={36+\overline{AD}^2-9\over 12\overline{AD}} \\ \cos \angle DAC = {\overline{AC}^2 +\overline{AD}^2-\overline{DC}^2 \over 2\times \overline{AC}\times \overline{AD}} ={16+\overline{AD}^2-4 \over 8\overline{AD}}} \Rightarrow {27+\overline{AD}^2\over 12\overline{AD}} ={12+\overline{AD}^2 \over 8\overline{AD}} \Rightarrow \overline{AD}=3\sqrt 2\\(A)\times: \cases{\angle AEB= \angle C\\ \angle AEC=\angle B} \Rightarrow {6\over \sin \angle C} ={4\over \sin \angle B} \Rightarrow \sin \angle C: \sin \angle B=3:2 \ne \angle C:\angle B\\(B)\times: \cases{\angle AEB =\angle ACD(對同弧的圓周角)\\ \angle ADC=\angle BDE} \Rightarrow \triangle ADE \sim \triangle BDE \Rightarrow {\overline{AD} \over \overline{DC}} ={\overline{BD} \over \overline{DE}} \\\qquad \Rightarrow {3\sqrt 2\over 2} ={3\over \overline{DE}} \Rightarrow \overline{DE}=\sqrt 2 \Rightarrow \overline{AD}:\overline{DE}= 3\sqrt 2: \sqrt 2 = 3:1 \ne 3:2\\ (C)\bigcirc: \overline{AD}\times \overline{AE} =3\sqrt 2\times (3\sqrt 2+\sqrt 2)=24\\ (D)\bigcirc: \cos \angle A={36+16-25\over 2\times 6\times 4}={9\over 16} \Rightarrow \sin \angle A={5\sqrt 7\over 16} \Rightarrow 2R={\overline{BC}\over \sin \angle A} ={5\over 5\sqrt 7/16} ={16\over \sqrt{7}}= {16\sqrt 7\over 7}\\ \qquad 最長的\overline{AP} = 直徑=2R ={16\sqrt 7\over 7}\\,故選\bbox[red, 2pt]{(CD )}$$
解:
$$\cases{AB=\begin{bmatrix}2& 2\\ -2& 6\end{bmatrix} \\AC=\begin{bmatrix}5& 1\\ -13& 3\end{bmatrix}} \Rightarrow D=AB+AC= A(B+C)=\begin{bmatrix}7& 3\\ -15& 9\end{bmatrix} \\ \Rightarrow A^{-1}D= B+C=A^{-1}\begin{bmatrix}7& 3\\ -15& 9\end{bmatrix} \\(A)\times: A=\begin{bmatrix}2& 0\\ 0& 1\end{bmatrix} \Rightarrow A^{-1}=\begin{bmatrix}1/2& 0\\ 0& 1\end{bmatrix} \Rightarrow A^{-1}\begin{bmatrix}7& 3\\ -15& 9\end{bmatrix}有非整數元素 \\(B)\bigcirc: A=\begin{bmatrix}3& -1\\ 1& 1\end{bmatrix} \Rightarrow A^{-1}=\begin{bmatrix}1/4& 1/4\\ -1/4& 3/4\end{bmatrix} \Rightarrow A^{-1}\begin{bmatrix}7& 3\\ -15& 9\end{bmatrix}= \begin{bmatrix}-2& 3\\ -13& 6\end{bmatrix} \\(C)\times: A=\begin{bmatrix}-3 & 1\\ 2& 1\end{bmatrix} \Rightarrow A^{-1}=\begin{bmatrix}-1/5& 1/5\\ 2/5& 3/5\end{bmatrix} \Rightarrow A^{-1}\begin{bmatrix}7& 3\\ -15& 9\end{bmatrix}有非整數元素\\(D)\bigcirc: A=\begin{bmatrix}1& -1\\ 1& 1\end{bmatrix} \Rightarrow A^{-1}=\begin{bmatrix}1/2& 1/2\\ -1/2& 1/2\end{bmatrix} \Rightarrow A^{-1}\begin{bmatrix}7& 3\\ -15& 9\end{bmatrix}= \begin{bmatrix}-4 & 6\\ -11& 3\end{bmatrix}\\,故選\bbox[red, 2pt]{(BD )}$$
第二部份:綜合題
一、填充題
解:
$$f(n)=1^n-2^n+3^n-4^n+ \cdots + 2015^n-2016^n+ 2017^n\\ \Rightarrow \cases{f(1)=1+(-2+3)+(-4+5)+\cdots+(-2016+2017)=1+2016 \div 2=1009 \\ f(2)=1^2+(3^2-2^2)+(5^2-4^2)+\cdots +(2017^2-2016^2)=1+5+9+\cdots +4033\\ \qquad =(4033+1)\times 1009\div 2 =2017\times 1009\\ f(3)= \sum_{k=1}^{1009}(2k-1)^3 -\sum_{k=1}^{1008}(2k)^3=\sum_{k=1}^{1008}\left( (2k-1)^3 -(2k)^3\right) +2017^3 \\ \qquad =2017^3-\sum_{k=1}^{1008}\left( 12k^2 -6k+1 \right) =2017^3-(2\times 1008\times 1009\times 2017-3\times 1008\times 1009+ 1008) \\ \qquad =(1008+1009)^3 -(2\times 1008\times 1009\times 2017-3\times 1008\times 1009+ 1008) \\ \qquad =1008^3+1009^3+3\times 1008\times 1009\times 2017-(2\times 1008\times 1009\times 2017-3\times 1008\times 1009+ 1008)\\ \qquad =1008^3+1009^3+ 1008\times 1009\times 2017 +3\times 1008\times 1009- 1008 \\\qquad =1008^3+1009^3+ 1008\times 1009\times 2020-1008= 1008(1008^2-1^2) +1009^3+ 1008\times 1009\times 2020 \\ \qquad =1009^3 +1008\times 1009\times 3027 = 1009^3 +(1009-1)\times 1009\times 3027 \\ \qquad =1009^3+1009^2\times 3027-1009\times 1009\times 3 =1009^2(1009+3027-3)=1009^2\times 4033} \\ \Rightarrow {f(1)f(2)\over f(3)} = {1009^2\times 2017 \over 1009^2\times 4033 } =\bbox[red,2pt]{2017\over 4033}$$
解:
$$餘弦定理:\cos \angle A={\overline{AD}^2 +\overline{AB}^2 -\overline{BD}^2 \over 2\times \overline{AD}\times \overline{AB}} \Rightarrow -{1\over 2}={46^2+13^2 -\overline{BD}^2 \over 2\times 46\times 13} \Rightarrow \overline{BD}=31\sqrt 3 \\正弦定理: {\overline{BD} \over \sin \angle C}= {31\sqrt 3\over \sqrt 3/2}=62=2R =\overline{AC}(\because \overline{AC}為ABCD外接圓的直徑)\\ \Rightarrow \overline{AC}=\bbox[red, 2pt]{62}$$
解:
$$\cases{A(4,-4,4)\\ B(2,0,0) \\ C(-1,0,-3) \\ D(a,b,c)} \Rightarrow \cases{\overrightarrow{AB}=(-2,4,-4) \\ \overrightarrow{CD}= (a+1,b,c+3) \\\overline{BC}=\sqrt{18}},由\overrightarrow {AB} \parallel \overrightarrow{CD} \Rightarrow {a+1\over -2} = {b\over 4} ={c+3\over -4}=t \\\Rightarrow D(t-1,-2t,2t-3);\\等腰\Rightarrow \overline{AD}=\overline{BC} =\sqrt{18} \Rightarrow (t-5)^2+(-2t+4)^2+ (2t-7)^2=18 \Rightarrow 9t^2-54t+90=18\\ \Rightarrow t^2-6t+8=0 \Rightarrow \cases{t=4\\t=2} \Rightarrow \cases{D(3,-8,5) \\ D(1,-4,1)} \Rightarrow \cases{\overrightarrow{AD}= (-1,-4,1) \\ \overrightarrow{AD}= (-3,0,-3)= \overrightarrow{BC}(不合)}\\ \Rightarrow \bbox[red,2pt]{D(3,-8,5)}$$
解:
$$假設圓內接12邊形邊長依序為2,3,2,3,\dots,則該12邊形內含一個正六邊形,如上圖;\\先求12邊形內角度數,即\angle AGB=?\\令\angle AOG=\theta \Rightarrow \angle BOG=60-\theta \Rightarrow \cases{\angle OAG= \angle OGA =(180^\circ-\theta)\div 2=90^\circ-\theta/2 \\ \angle OBG=\angle OGB=(180^\circ-(60^\circ-\theta))\div 2=60^\circ+\theta/2} \\ \Rightarrow \angle AGB= \angle OGA+\angle OGB = 90^\circ-\theta/2+60^\circ+\theta/2=\color{blue}{150^\circ}\\ \triangle GAB \Rightarrow \cos 150^\circ = {3^2+2^2-\overline{AB}^2 \over 2\times 2\times 3} \Rightarrow -{\sqrt 3\over 2} ={13-\overline{AB}^2 \over 12} \Rightarrow \overline{AB}^2= 13+6\sqrt 3\\ \Rightarrow 12邊形面積=6\triangle GAB+6\triangle OAB =6\left({1\over 2}\times 3\times 2\sin 150^\circ +{1\over 2}\times \overline{AB}\times \overline{AB}\sin 60^\circ\right)\\ =6\left( {3\over 2}+{\sqrt 3\over 4}(13+6\sqrt 3)\right) =9+{39\sqrt 3\over 2}+27 =\bbox[red, 2pt]{36+{39\over 2}\sqrt 3}$$
$$\sum_{k=1}^\infty {1\over k^3+8k^2+15k} = \sum_{k=1}^\infty {1\over k(k+3)(k+5)} =\sum_{k=1}^\infty \left({1\over 15}\cdot {1\over k}-{1\over 6} \cdot {1\over k+3}+{1\over 10}\cdot {1\over k+5} \right) \\={1\over 15}({1\over 1} +{1\over 2} +{1\over 3} +{1\over 4} +{1\over 5}) -{1\over 6}({1\over 4} +{1\over 5}) +\sum_{k=1}^\infty \left({1\over 15}\cdot {1\over k+5}-{1\over 6} \cdot {1\over k+5}+{1\over 10}\cdot {1\over k+5} \right) \\={1\over 15} \times {60+30+20+ 15+12 \over 60} -{1\over 6}\times {5+4\over 20} +0 ={1\over 15} \times {137 \over 60} -{1\over 6}\times {9\over 20} = \bbox[red, 2pt]{139\over 1800}$$
解:
$$\cases{S_2:(x-1)^2+(y-2)^2+(z-3)^2 \le 9\Rightarrow \cases{球心O_1(1,2,3)\\ 球半徑R=3} \\S_1:(x-1)^2+(y-2)^2+z^2 \le 4\Rightarrow \cases{球心O_2(1,2,0)\\ 球半徑r=2}} \Rightarrow d=\overline{O_1O_2}=3\\ 相交體積={\pi \over 12d}(R+r-d)^2(d^2+2dr-3r^2+2dR+6rR-3R^2)\\ ={\pi \over 12\times 2}(3+2-3)^2(9+12-12+18+36-27)=\bbox[red,2pt]{4\pi}\\公式來源:\href{https://mathworld.wolfram.com/Sphere-SphereIntersection.html}{按這裡}$$
解:
$$|z|=2 \Rightarrow z=2(\cos \theta+i\sin \theta) \Rightarrow |z^2-2z+8|= |z^2-2z+2z\bar z|= |z||z-2+2\bar z| \\ =2| 2(\cos \theta+i\sin \theta)-2+4(\cos \theta-i\sin \theta)| =2|6\cos \theta-2-i\cdot 2\sin\theta| \\ =2\sqrt{(6\cos \theta-2)^2 +4\sin^2 \theta} =2\sqrt{36\cos^2\theta -24\cos\theta+4\sin^2 \theta +4} =2\sqrt{32\cos^2\theta -24\cos\theta+ 8} \\ =4\sqrt{ 8\cos^2\theta -6\cos \theta+2}= 4\sqrt{ 8(\cos^2\theta -{3\over 4}\cos \theta+{9\over 64})+2-{9\over 8}} =4\sqrt{ (\cos\theta-{3\over 8})^2+{7\over 8}} \\ \Rightarrow |z^2-2z+8|的最小值=4 \sqrt{7\over 8} = \bbox[red, 2pt]{\sqrt{14}}$$
解:
$$令\cases{L_1:y=2x-7 \\ L_2: y={1\over 2}x-3 \\ L_3\parallel L_1且L_3與拋物線相切} \Rightarrow L_3: y=2x+k代入拋物線\Rightarrow x^2+2x-1=2x+k \\\Rightarrow x^2-k-1=0恰有一解\Rightarrow k=-1 \Rightarrow L_3:y=2x-1\\ \Rightarrow \cases{L_3與L_2相交於A(-{4\over 3},-{11\over 3}) \\ L_1與L_2相交於B({8\over 3},-{5\over 3})} \Rightarrow 拋物線移動的方向\overrightarrow{AB} =(4,2) \\\Rightarrow 拋物線原頂點(-1,-2)移動後變為(-1,-2)+\overrightarrow{AB}=(3,0) \Rightarrow 拋物線方程式變為y=(x-3)^2\\ \Rightarrow \bbox[red, 2pt]{y=x^2-6x+9}$$
解:
$$L:x-y+5=0 \Rightarrow 斜率m=1 \Rightarrow Q為切點且切線斜率=m=1;\\ x=\sqrt{{9\over 4}y^2+9} \Rightarrow y=\sqrt{{4\over 9}x^2 -4} \Rightarrow y'= {4x \over 9\sqrt{{4\over 9}x^2 -4}} =1 \Rightarrow x= {9\over \sqrt 5} \Rightarrow y= {4\over \sqrt 5} \\ \Rightarrow Q({9\over \sqrt 5},{4\over \sqrt 5}) \Rightarrow \overline{PQ}最小值= \text{dist}(Q,L)={\sqrt 5+5\over \sqrt 2} = \bbox[red, 2pt]{\sqrt{10}+ 5\sqrt 2\over 2}$$
二、計算證明題
解:
(1)$$(\sqrt 2-1)^2=3-2\sqrt 2 \Rightarrow (\sqrt 2-1)^4= (3-2\sqrt 2)^2 =17-12\sqrt 2 \\ \Rightarrow (\sqrt 2-1)^5= (17-12\sqrt 2)(\sqrt 2-1)=29\sqrt 2-41 = \sqrt{29^2\times 2} -\sqrt{41^2} \\ =\sqrt{1682}-\sqrt{1681} =\sqrt{m+1} -\sqrt m \Rightarrow \bbox[red, 2pt]{m=1681}$$(2)$$用歸納證明法: 證明(\sqrt 2-1)^{2n-1}=\sqrt{a_n+1}-\sqrt {a_n},其中n,a_n\in N\\n=1時,a_n=1,顯然成立;\\假設n=k時成立,即(\sqrt 2-1)^{2k-1}=\sqrt{a_k+1}-\sqrt {a_k},其中k,a_k\in N;\\ 當n=k+1時,(\sqrt 2-1)^{2k+1}= (\sqrt{a_k+1}-\sqrt {a_k})(\sqrt 2-1)^2 = (\sqrt{a_k+1}-\sqrt {a_k})(3-2\sqrt 2) \\ =(3\sqrt{a_k+1} +2\sqrt{2a_k})-(2\sqrt{2a_k+2}+3\sqrt {a_k})\\ \Rightarrow \cases{左式^2=17a_k+9+12\sqrt{2a_k^2+2a_k} \\ 右式^2=17a_k+8 +12\sqrt{2a_k^2+2a_k}} \Rightarrow 左式^2-右式^2=1 \Rightarrow n=k+1時亦成立;\\因此當n=1009時,存在正整數m(a_{1009})滿足(\sqrt 2-1)^{2017} =\sqrt{m+1}-\sqrt m$$
解:
$$延長直線\overline{AD}交\triangle ABC外接圓於E點,見上圖;\\ \cases{\angle BAD=\angle BCE(對同弧的圓周角) \\ \angle ADB = \angle CDE} \Rightarrow \triangle ABD \sim \triangle CED \Rightarrow {\overline{BD} \over \overline{DE} }= {\overline{AD} \over \overline{DC} }\\ \qquad \qquad \Rightarrow \overline{AD}\times \overline{DE} =\overline{BD}\times \overline{DC}\cdots (1)\\ \cases{\angle BAD=\angle DAC\\ \angle B=\angle E(對同弧的圓周角)} \Rightarrow \triangle ABD \sim \triangle AEC \Rightarrow {\overline{AB} \over \overline{AE}} ={\overline{AD} \over \overline{AC}} \Rightarrow \overline{AB} \times \overline{AC} =\overline{AD}\times \overline{AE} \\ = \overline{AD}(\overline{AD}+\overline{DE}) = \overline{AD}^2 + \overline{AD}\times \overline{DE} =\overline{AD}^2 +\overline{BD}\times \overline{DC}(由(1)) \\ \Rightarrow \overline{AD}^2 =\overline{AB} \times \overline{AC} -\overline{BD}\times \overline{DC} \Rightarrow \overline{AD}=\sqrt{ \overline{AB} \times \overline{AC} -\overline{BD}\times \overline{DC}},故得證。$$
解:
$$(1)f'(x)=0有實數解\Rightarrow 3x^2-2ax+b=0 的判別式4a^2-12b\ge 0,即\bbox[red, 2pt]{a^2\ge 3b} \\(2)f'(-1)=f'(3)=0 \Rightarrow f'(x)=k(x+1)(x-3)= 3x^2-2ax+b \\\Rightarrow kx^2-2kx-3k= 3x^2-2ax+b \Rightarrow \cases{k=3\\ a=6 \\b=-9} \Rightarrow f(x)=x^3-6x^2-9x+c\\ f(x)為3次式,圖形為左下右上 \Rightarrow \cases{f(-1)> 0 \\ f(3)< 0} \Rightarrow \cases{c> -5 \\ c< 27} \Rightarrow \bbox[red, 2pt]{-5 < c < 27}$$
-- END (僅供參考) --












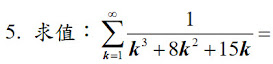









謝謝您,馬上就有了耶😄
回覆刪除