桃園市立高級中等學校109學年度教師聯合甄選筆試試題-數學科
第壹部分:填充題
$$令t=x^2 \Rightarrow x^4+(m-5)x^2+(m+3)=0 有相異4實根,相當於t^2+(m-5)t+(m+3)=0有相異2正根\\ \Rightarrow \cases{判別式>0\\ 兩根之和>0 \\ 兩根之積>0} \Rightarrow \cases{(m-5)^2-4(m+3) > 0 \\ 5-m > 0 \\ m+3 >0} \Rightarrow \cases{m> 13或m< 1\\ m< 5\\ m> -3} \Rightarrow \bbox[red,2pt]{-3 < m < 1}$$
$$-8\le \log{4^n\over 15^n} < -7 \Rightarrow -8\le 2n\log 2-n(\log 3+1-\log 2) < -7 \\\Rightarrow -8\le n(3\log 2-\log 3-1) < -7 \Rightarrow -8\le n(3\times 0.301-0.4771-1) < -7 \\ \Rightarrow -8 \le -0.5741n < -7 \Rightarrow 12.2 < n \le 13.93 \Rightarrow n=\bbox[red,2pt]{13}$$
$$\begin{array}{} 第1筒& 第2筒 & 第3筒 & 數量\\\hline
1 & 1& 4 & C^6_1C^5_1\\ & 2 & 3& C^6_1C^5_2\\ & 3& 2 & C^6_1C^5_3\\ & 4 & 1& C^6_1C^5_4\\\hdashline
2 & 1& 3& C^6_2C^4_1 \\ & 2& 2& C^6_2C^4_2\\ & 3& 1 & C^6_2C^4_3 \\\hdashline
3 & 1 & 2& C^6_3C^3_1\\ & 2& 1& C^6_3C^3_2\\\hdashline4 & 1 & 1& C^6_4C^2_1 \\\hline\end{array}\\ \Rightarrow 共有6(5+10+10+5) +15(4+6+4)+ 20(3+3)+ 15\times 2 \\ =180+210+120+30 =\bbox[red,2pt]{540}分法$$
1 & 1& 4 & C^6_1C^5_1\\ & 2 & 3& C^6_1C^5_2\\ & 3& 2 & C^6_1C^5_3\\ & 4 & 1& C^6_1C^5_4\\\hdashline
2 & 1& 3& C^6_2C^4_1 \\ & 2& 2& C^6_2C^4_2\\ & 3& 1 & C^6_2C^4_3 \\\hdashline
3 & 1 & 2& C^6_3C^3_1\\ & 2& 1& C^6_3C^3_2\\\hdashline4 & 1 & 1& C^6_4C^2_1 \\\hline\end{array}\\ \Rightarrow 共有6(5+10+10+5) +15(4+6+4)+ 20(3+3)+ 15\times 2 \\ =180+210+120+30 =\bbox[red,2pt]{540}分法$$
$$u=\sqrt {x+4} \Rightarrow du ={1\over 2\sqrt{x+4}}\;dx = {1\over 2u}\;dx \Rightarrow \int_5^{12} {\sqrt{x+4}\over x}\;dx =\int_3^4 {u\over u^2-4}\cdot 2u\;du \\ =\int_3^4 {2u^2\over u^2-4}\;du = \int_3^4 \left(2+{8\over u^2-4}\right)\;du= \int_3^4 \left(2+{2\over u-2} -{2\over u+2}\right)\;du\\ =\left. \left[2u +2\ln(u-2)-\ln(u+2) \right] \right|_3^4 =(8+2\ln 2-2\ln 6)-(6+2\ln 1-2\ln 5)\\=8+2\ln 2-2\ln 3-2\ln 2-6+2\ln 5 =2+ 2(\ln 5-\ln 3)=\bbox[red,2pt]{2+2\ln {5\over 3}}$$
解:
$$e^n= \sum_{k=0}^\infty {n^k \over k!}=1+n+{n^2\over 2!}+{n^3\over 3!}+\cdots; \\{k^2\over k!}= {k\over (k-1)!} = {(k-1)+1\over (k-1)!} = {1\over (k-2)!} +{1\over (k-1)!}\\由上二式可知:\sum_{k=2}^n{n^k+k^2 \over k!} =\left({n^2\over 2!}+ {n^3\over 3!}+ {n^4\over 4!}+\cdots \right) + \left((1+1)+ (1+{1\over 2!})+ ({1\over 2!}+ {1\over 3!})\cdots \right) \\=(e^n-n-1)+(e^1+e^1-1) \Rightarrow \lim_{n\to \infty}e^{-n}\sum_{k=2}^n{n^k+k^2 \over k!} =\lim_{n\to \infty}e^{-n}(e^n-n+2e-2) \\ =\lim_{n\to \infty} \left( 1-{n\over e^n}+ {2e\over e^n} -{2\over e^n}\right) =1-0+0-0= \bbox[red,2pt]{1}$$
$$令p(n)代表擲n次銅板,才出現連續兩次反面的機率;\\因此\cases{第1次出現正面,\color{blue}{後n-1次才出現連續兩次反面}\\ 第1次出現反面第2次出現正面,\color{blue}{後n-2次才出現連續兩次反面}} \\\Rightarrow p(n)={1\over 2}p(n-1) +{1\over 4}p(n-2);\\ 由於\cases{p(1)=0\\ p(2)=p(\{反反\})=1/4} \Rightarrow \cases{p(1)=0\\ p(2)=1/4\\ p(n)={1\over 2}p(n-1) +{1\over 4}p(n-2),n\ge 3}\\ \Rightarrow E(X)=\sum_{k=1}^\infty kp(k) =1\cdot 0+2\cdot {1\over 4}+\sum_{k=3}^\infty kp(k) ={1\over 2}+\sum_{k=3}^\infty ({1\over 2}kp(k-1)+ {1\over 4}kp(k-2)) \\= {1\over 2}+{1\over 2}(1+E(X)) +{1\over 4}(2+E) = {3\over 2}+ {3\over 4}E(X) \Rightarrow {1\over 4}E(X)= {3\over 2} \Rightarrow \bbox[red,2pt]{E(X)=6}\\ E(X^2)= \sum_{k=1}^\infty k^2p(k) =1^2\cdot 0 + 2^2\cdot {1\over 4}+\sum_{k=3}^\infty k^2p(k)=1 +\sum_{k=3}^\infty \left( {1\over 2}k^2p(k-1) +{1\over 4}k^2p(k-2)\right) \\ =1 +\sum_{k=3}^\infty \left( {1\over 2}((k-1)^2p(k-1) +2(k-1)p(k-1)+p(k-1))\\ \qquad +{1\over 4}((k-2)^2p(k-2) +4(k-2)p(k-2)+4p(k-2))\right)\\ \\=1+{1\over 2}(E(X^2)+2E(X)+1) +{1\over 4}(E(X^2)+4E(X)+4)\\=1+{1\over 2}(E(X^2)+13) +{1\over 4}(E(X^2)+28) ={29\over 2}+ {3\over 4}E(X^2) \Rightarrow E(X^2)=58 \\\Rightarrow Var(X)= E(X^2)-(E(X))^2 = 58-6^2=22 \Rightarrow \bbox[red,2pt]{Var(X)=22}$$
$$\cases{(1-\sqrt 3)^n=a_n+b_n\sqrt 3 \cdots(1)\\ (1+\sqrt 3)^n=a_n-b_n\sqrt 3\cdots(2)}\Rightarrow \cases{(1)+(2) =(1-\sqrt 3)^n + (1+\sqrt 3)^n=2a_n \\ (1)-(2)= (1-\sqrt 3)^n - (1+\sqrt 3)^n=2b_n\sqrt 3} \\ \Rightarrow \cases{a_n= ((1-\sqrt 3)^n + (1+\sqrt 3)^n)\div 2 \\ b_n= ((1-\sqrt 3)^n - (1+\sqrt 3)^n)\div (2\sqrt 3)} \Rightarrow {b_n\sqrt 3\over a_n} ={(1-\sqrt 3)^n - (1+\sqrt 3)^n \over (1-\sqrt 3)^n + (1+\sqrt 3)^n} \\ ={\left({1-\sqrt 3 \over 1+\sqrt 3} \right)^n-1 \over \left({1-\sqrt 3 \over 1+\sqrt 3} \right)^n+1} \Rightarrow \lim_{n\to \infty}{b_n\sqrt 3\over a_n} =-1 \Rightarrow \lim_{n\to \infty}{b_n\over a_n}=-{1\over \sqrt 3} =\bbox[red,2pt]{-{\sqrt 3\over 3}}$$
$$令\cases{首項a_1=a\\ 公差d},則a_2,a_4,a_7成等比\Rightarrow a_4^2 = a_2a_7 \Rightarrow (a+3d)^2 =(a+d)(a+6d) \\ \Rightarrow a^2+6ad+9d^2 = a^2+7ad+6d^2 \Rightarrow ad-3d^2=0 \Rightarrow d(a-3d)=0 \Rightarrow a=3d (d \ne 0);\\ a_1+\cdots+a_k > 100a_1 \Rightarrow (2a+(k-1)d)k \div 2 > 100a \Rightarrow (6d+kd-d)k > 600d \\ \Rightarrow (k+5)k > 600 \Rightarrow k\ge \bbox[red,2pt]{23}$$
$$假設有n位選手,需比賽C^n_2場次,其中有a場次分出勝負,另有C^n_2-a場次平手;\\無論是否分出勝負,兩位選手得分合計皆是2,\\因此全部選手得分總計為2a+2(C^n_2-a)=2C^n_2 = n(n-1);\\取n=13 \Rightarrow 13\times 12=156,因此共有\bbox[red,2pt]{13}位選手參加$$
$$C^n_0+C^n_1+C^n_2 = \bbox[red,2pt]{n^2+n+2\over 2}\\公式來源:\href{http://www.sec.ntnu.edu.tw/Monthly/101(346-355)/347-PDF/04-100044-%E5%B9%B3%E9%9D%A2%E5%88%86%E5%89%B2%E5%85%AC%E5%BC%8F%E4%B9%8B%E6%BC%94%E7%AE%97(%E6%9C%88%E5%88%8A).pdf}{按這裡}$$
解:
$$f(x)=a\tan^3(x) +b\cos\left({\pi \over 2}-x \right)+1 =a\tan^3(x) +b\sin(x)+1 \\由題意知:f(3)=5 \Rightarrow a\tan^3(3) +b\sin(3)+1=5 \Rightarrow a\tan^3(3) +b\sin(3)=4\\ 現在 f(2\pi-3) =a\tan^3(-3) +b\sin(-3)+1 =-(a\tan^3(3) +b\sin(3))+1 =-4+1= \bbox[red, 2pt]{-3}$$
$$\cfrac{x^2+{1\over 5}y^2}{2} \ge \sqrt{{1\over 5}x^2y^2} ={1\over \sqrt 5}xy \Rightarrow x^2+{1\over 5}y^2\ge {2\over \sqrt 5}xy\cdots(1)\\同理, \cfrac{{4\over 5}y^2+z^2}{2} \ge \sqrt{{4\over 5}y^2z^2} ={2\over \sqrt 5}yz \Rightarrow {4\over 5}y^2+z^2 \ge {4\over \sqrt 5}yz\cdots(2)\\ (1)+(2) \Rightarrow x^2+y^2+z^2 \ge {2\over \sqrt 5}(xy+2yz) \Rightarrow {xy+2yz\over x^2+y^2+z^2} \le {\sqrt 5\over 2} \Rightarrow 最大值為 \bbox[red,2pt]{\sqrt 5\over 2}$$
第貳部份:計算或證明題
解:(a)$$2a_{n+1}= a_n^2-2a_n+4 =(a_n-1)^2+3 \Rightarrow a_{n+1}={1\over 2}(a_n-1)^2+{3\over 2} \\\Rightarrow |a_n-1| \le 1,即0 \le a_n \le 2,則數列收斂;\\也就是\bbox[red,2pt]{0\le a_1 \le 2},則數列收斂至{1\over 2}+{3\over 2}=2,即\bbox[red,2pt]{\lim_{n\to \infty} a_n=2}$$(b)$$2a_{n+1}= a_n^2-2a_n+4 \Rightarrow 2a_{n+1}-4=a_n^2-2a_n \Rightarrow 2(a_{n+1}-2)=a_n(a_n-2)\\ \Rightarrow {1\over 2(a_{n+1}-2) }={ 1\over a_n(a_n-2)} ={1\over 2}\left({1\over a_n-2}-{1\over a_n} \right) \Rightarrow {1\over a_{n+1}-2 }= {1\over a_n-2}-{1\over a_n} \\ \Rightarrow \cases{ {1\over a_2-2} = {1\over a_1-2}-{1\over a_1} \\ {1\over a_3-2} = {1\over a_2-2} -{1\over a_2} \\ \cdots \cdots \\ {1\over a_n-2} = {1\over a_{n-1}-2}-{1\over a_{n-1}} \\ {1\over a_{n+1}-2} = {1\over a_{n}-2}-{1\over a_{n}}} \Rightarrow 左式全部相加\Rightarrow {1\over a_{n+1}-2}= {1\over a_1-2}- \sum_{k=1}^n {1\over a_k} \\ \Rightarrow \lim_{n\to \infty}{1\over a_{n+1}-2}= {1\over a_1-2}- \sum_{n=1}^\infty {1\over a_n}=-{1\over 4}- \sum_{n=1}^\infty {1\over a_n}\\ 由於a_1=-2 \not \in [0,2],因此\lim_{n\to \infty} a_{n+1} =\infty \Rightarrow \lim_{n\to \infty}{1\over a_{n+1}-2}=0\\ \Rightarrow -{1\over 4}- \sum_{n=1}^\infty {1\over a_n}=0 \Rightarrow \sum_{n=1}^\infty {1\over a_n} =\bbox[red,2pt]{-{1\over 4}}$$
解:
$$\angle AOB=\theta \Rightarrow \cos \theta = {\overline{OB}^2 +\overline{OA}^2 -\overline{AB}^2\over 2\overline{OA}\times\overline{OB}} = {5-\overline{AB}^2\over 4} \Rightarrow \overline{AB}^2 =5-4\cos\theta;\\四邊形OACB= \triangle OAB+ 正\triangle ABC = {1\over 2}\overline{OA}\times \overline{OB}\sin \theta+{\sqrt 3\over 4}\overline{AB}^2 =\sin \theta+ {5\sqrt 3\over 4}-\sqrt 3\cos \theta \\ ={5\sqrt 3\over 4}+2({1\over 2}\sin \theta-{\sqrt 3\over 2}\cos \theta) = {5\sqrt 3\over 4}+2(\cos(-60^\circ)\sin \theta+\sin(-60^\circ) \cos \theta) \\= {5\sqrt 3\over 4}+2\sin(\theta-60^\circ) \Rightarrow 當\theta-60^\circ=90^\circ 時,即\theta=150^\circ,該四邊形面積有最大值={5\sqrt 3\over 4}+2\\ \Rightarrow (a)\bbox[red,2pt]{\angle AOB=150^\circ}\;(b)\bbox[red,2pt]{2+{5\sqrt 3\over 4}}$$
$$f(x)=3x^5+7x-3 \Rightarrow f'(x)=15x^4+7 > 0, \forall x\in R \Rightarrow f(x) 為嚴格遞增;\\ 又\cases{f(0)=-3 <0 \\ f(1)=7 > 0\\f(1/2)>0} \Rightarrow f(x)=0恰有一根r,且0< r< 1/2;\\ \Rightarrow 3r^5+7r-3=0 \Rightarrow 7r =3(1-r^5) \Rightarrow {3\over 7} = {r\over 1-r^5} = r+r^6+r^{11}+\cdots \\ \Rightarrow 存在一數列\{a_n=5n-4\}使得{7\over 3} =r^{a_1} +r^{a_2} +r^{a_3} +\cdots ;\\唯一性:\\若存在另一數列\{b_n\},使得r^{a_1} +r^{a_2} +r^{a_3} +\cdots =r^{b_1} +r^{b_2} +r^{b_3} +\cdots\\ 將兩數列相同的部份扣除,剩下r^{c_1} +r^{c_2} +r^{c_3} +\cdots =r^{d_1} +r^{d_2} +r^{d_3} +\cdots\\,其中\{c_n\},\{d_n\}仍為嚴格遞增正整數數列;\\若c_1 < d_1 \Rightarrow 1\le d_1-c_1且2\le d_2-c_1且3 \le d_3-c_1\dots \\ \Rightarrow r^{c_1} < r^{c_1} +r^{c_2} +r^{c_3} +\cdots =r^{d_1} +r^{d_2} +r^{d_3} +\cdots \\ \Rightarrow r^{c_1} < r^{d_1} +r^{d_2} +r^{d_3} +\cdots \\\Rightarrow 1 < r^{d_1-c_1} +r^{d_2-c_1} + r^{d_3-c_1}+\cdots \le r^1+r^2+r^3 +\cdots = {r\over 1-r}<1 (\because 0< r<1/2)\\ \Rightarrow 1 < 1矛盾;\\同理,若c_1> d_1也矛盾;\\因此c_1=d_1,即\{a_n\}=\{b_n\},唯一性得證。$$
-- END (僅供參考) --







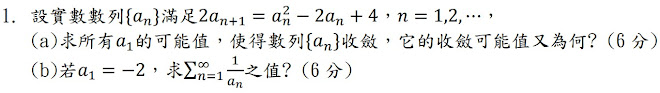


請問有私人email嗎?想私下請教一些問題,謝謝。
回覆刪除chu246@gmail.com
刪除第四題的最後有點錯誤
回覆刪除應該是2+2(ln2−ln6+ln5)
謝謝你
謝謝提醒,已修訂!!
刪除