110年國中教育會考-數學詳解

110年國中教育會考 數學科

解答：$$(x,y)在第二象限\Rightarrow x\lt 0且y\gt 0，故選\bbox[red, 2pt]{(A)}$$

解答：$$(-8) + (-2)\times (-3)= (-8)+6=-2，故選\bbox[red, 2pt]{(B)}$$

解答：$$\cases{x=4y\cdots(1) \\6y-x=10\cdots}，將(1)代入(2)得6y-4y=10 \Rightarrow 2y=10 \Rightarrow y=5\\將y=5代回(1)可得x=4\times 5=20； 因此\cases{x=20=a\\ y=5=b} \Rightarrow a+b=20+5=25，故選\bbox[red, 2pt]{(D)}$$

解答：$$\triangle ABD = 矩形ABCD\div 2=20\div 2=10；\triangle ADE=\triangle BDE-\triangle ABD = 24-10=14\\，故選\bbox[red, 2pt]{(C)}$$

解答：$${5^6\over 5^3}=5^{6-3}=5^3=125，故選\bbox[red, 2pt]{(D)}$$

解答：$$(C) 4\sqrt 3\times 2\sqrt 3=4\times 2\times (\sqrt 3)^2= 8\times 3=24\ne 8\sqrt 3，故選\bbox[red, 2pt]{(C)}$$

解答：$$(A)\times: 第2分鐘的海拔是200，第4分鐘的海拔約175公尺，是在下降中\\(B)\bigcirc:起點海拔50，終點海拔350公尺，終點比起點高350-50=300公尺；\\\qquad 且第4分鐘至第8分鐘都在上升中；\\(C)\times: 終點比起點高350-50=300公尺\\(D)\times:終點比起點高350-50=300公尺\\，故選\bbox[red, 2pt]{(B)}$$

解答：$$(A)\times: 300^2=(248+52)^2 = 248^2+2\times 248\times 52+52^2 \\(B) \times:200^2= (248-48)^2= 248^2-2\times 248\times 48 +48^2 \\(C)\bigcirc: \\(D)\times:200^2= (248-48)^2= 248^2-2\times 248\times 48 +48^2\\，故選\bbox[red, 2pt]{(C)}$$

解答：$$由圖形可知:\cases{6月:日\gt 美\gt 英\\ 7月:英\gt 美\gt 日\\8月:日\gt 英\gt 美\\9月:美\gt 日\gt 英}\qquad，故選\bbox[red, 2pt]{(C)}$$

解答：$$半徑r=6的圓周長= 2\pi r=12\pi，因此另一個扇形的弧長為12\pi-5\pi=7\pi \\弧長7\pi= r\theta= 6\theta \Rightarrow 圓心角\theta ={7\over 6}\pi = {7\over 6}\times 180^\circ = 210^\circ，故選\bbox[red, 2pt]{(D)}$$

解答：$$玩偶有二個(北極熊與獅子)，刮刮樂有100張，因此刮中玩偶的機率為{2\over 100}={1\over 50}\\，故選\bbox[red, 2pt]{(D)}$$

解答：$$美美買了5盒餅乾，花了5x元；得到3張摸彩券，因此300\le 5x \lt 400 \Rightarrow 60\le x\lt 80 \cdots(1)；\\小儀買了5盒餅乾及1個蛋糕，花了5x+150元；拿到4張摸獎券，因此400\le 5x+150\lt 500 \\\Rightarrow 250\le 5x \lt 350 \Rightarrow 50\le x\lt 70 \cdots(2)；\\ 取(1)與(2)的交集，也就是60\le x\lt 70，故選\bbox[red, 2pt]{(B)}$$

解答：$$假設公差為d，則a_{20}+a_{22} = (a_{21}-d)+(a_{21}+d)= 2a_{21} =0 \Rightarrow a_{21}=0；\\又a_1 \gt 0，因此\cases{a_1,a_2,\dots,a_{20} \gt 0 \\ a_{21}=0\\ a_{22},a_{23},\dots \lt 0}\\(A) \times: a_{21}+a_{22}=0+a_{22} =a_{22} \lt 0\\(B)\bigcirc:理由同(A)\\(C)\times: a_{21}\times a_{22}=0 \times a_{22}=0\\ (D)\times: 理由同(C)\\故選\bbox[red, 2pt]{(B)}$$

解答：$$將a,b,c全部變為負值或全部變為正值，其三數相加的對絕對值最大，故選\bbox[red, 2pt]{(C)}$$

解答：

$$\triangle ABC \cong \triangle DEF \Rightarrow \cases{\angle ACB= \angle DFE \Rightarrow \overline{EF} =\overline{EC} \\ \angle A = \angle D =40^\circ \Rightarrow \angle D \gt \angle CED \Rightarrow  \overline{EC}\gt \overline{CD}\cdots(1) \\ \overline{AC}=\overline{DF} \Rightarrow \overline{AE} +\overline{EC} =\overline{FC} +\overline{CD}\Rightarrow \overline{FC} \gt \overline{AE}(由(1)推得)}  \\ 因此\cases{\overline{EF}=\overline{EC} \\ \overline{FC} \ne \overline{AE}}，故選\bbox[red, 2pt]{(B)}$$

解答：$$\cases{飯糰A:a元\\ 飯糰B:a+4元} \Rightarrow 飯糰A +飯糰B+2瓶飲料=a+(a+4)+30 =2組優惠價(39元\times 2)\\ \Rightarrow 2a+34=78 \Rightarrow a=22\Rightarrow \cases{飯糰A:22元\\ 飯糰B:26元}；\\現在只想買1瓶飲料，也就是1組優惠價=飯糰B+飲料=39 \Rightarrow 26+ 飲料=39 \Rightarrow 飲料=13元\\，故選\bbox[red, 2pt]{(B)}$$

解答：

$$A為切點\Rightarrow \angle OAD=90^\circ，又\overline{AD} \parallel \overline{BC}，所以\overline{AE}\bot \overline{BC}\\ 直角\triangle AEB中，\angle B=58^\circ \Rightarrow \angle BAE=90^\circ -58^\circ = 32^\circ \Rightarrow \angle BAC = 32^\circ \times 2=64^\circ  \\ \Rightarrow \angle BOC = 64^\circ \times 2=128^\circ = \stackrel{\large \frown}{BC}，故選\bbox[red, 2pt]{(D)}$$

解答：$$y=(x+3)^2 向下移2單位\Rightarrow y=(x+3)^2-2，\\再往右移3單位 \Rightarrow y=(x+3-3)^2-2=x^2-2 \\\Rightarrow a=1,b=0,c=-2，故選\bbox[red, 2pt]{(A)}$$

解答：

$$令\angle DFE=a^\circ，由於\overline{FE}為對稱軸，所以\cases{\angle FDE=\angle C=40^\circ \\ \angle EFC=\angle DFE=a^\circ};\\ 又\overline{DE}為對稱軸，所以\cases{\angle BDE=\angle FDE=40^\circ \\\angle B=\angle DFE=a^\circ }；\\ 四邊形BCFD內角和=360^\circ = 3a+40\times 3 \Rightarrow a=80^\circ ，故選\bbox[red, 2pt]{(D)}$$

解答：$$由題意可知:乙租甲還的有4輛；因此從乙出租的車輛有13+4=17輛\\，而從甲出租的有15輛，故選\bbox[red, 2pt]{(B)}$$

解答：

$$\cases{\angle 1=\angle ABD+\angle ADB\\ \angle 3=\angle CBD+ \angle CDB} \Rightarrow \angle 1+\angle 3= (\angle ABD+ \angle CBD) + (\angle ADB+\angle CDB)=\angle ABC+ \angle D\\ \Rightarrow \angle 1+\angle 3=\angle ABC+ \angle D$$

$$若\angle D=180^\circ，即D'=D，則\cases{\angle 1=\angle B+\angle C\\ \angle 2=\angle A+\angle C\\ \angle 3= \angle A+\angle B}  \\\Rightarrow \angle 1+\angle 2+\angle 3=2(\angle A+\angle B+\angle C) =360^\circ \\ 由於\angle D \lt 180^\circ ，所以\angle 1+\angle 2+\angle 3 \lt 360^\circ (\angle A與\angle C都變大)，\\因此，故選\bbox[red, 2pt]{(A)}$$

解答：$$(A)\bigcirc: \cases{a=1\\ b=2^5\times 3^2\times 5} \Rightarrow 最大公因數=1\\(B) \bigcirc: \cases{a=2\times 3\\ b=2^4\times 3\times 5} \Rightarrow 最大公因數=6\\(C)\times:\cases{a=2^3=8\\ b=2^2\times 3^2\times 5} \Rightarrow 最大公因數=4 \\(D)\bigcirc: \cases{a=2^2\times 3\\ b=2^3\times 3 \times 5} \Rightarrow 最大公因數=12\\，故選\bbox[red, 2pt]{(C)}$$

解答：$$菱形邊長=\overline{AH} +\overline{HG} +\overline{GD} =8+5+4=17\\ \overline{GF} \parallel \overline{HC} \Rightarrow {\overline{GD} \over \overline{DH}} ={ \overline{DF} \over \overline{DC}} \Rightarrow {4\over 4+5} ={\overline{DF} \over 17}   \Rightarrow \cases{\overline{DF}=68/9 \\ \overline{CF}=85/9 } \Rightarrow \overline{CF} \gt \overline{FD}\\ 又 \overline{EC}= \overline{AH}= 8 \Rightarrow  \overline{BE}=\overline{BC}-\overline{EC}=17-8= 9 \Rightarrow \cases{\overline{EC}=8\\ \overline{BE}=9} \\ \Rightarrow \overline{CF} \gt \overline{BE} \gt \overline{EC} \gt \overline{DF}，故選\bbox[red, 2pt]{(A)}$$

解答：$$\cases{甲影印機每分鐘印a張 \\ 乙影印機每分鐘印b張}\quad ， 從10:00到10:15，甲印了15分鐘，乙印了10分鐘\\，兩台印量相同 ，即15a=10b\cdots(1)；\\到了10:45，甲印了45分鐘，乙印了40分鐘，合印2100張，即45a+40b=2100\cdots(2)；\\將(1)代入(2)，可得30b+40b=2100 \Rightarrow b=30 \Rightarrow a=20；\\若甲、乙兩台機器同時於10:00一起合印，花了x分鐘，合計2100張，即(a+b)x=2100 \\ \Rightarrow 50x=2100 \Rightarrow x=42 \Rightarrow 於10:42合印2100張，故選\bbox[red, 2pt]{(C)}$$

解答：

$$甲的作法(見上圖):P點在\overline{AC}的中垂線上，因此\overline{PA} =\overline{PC} \Rightarrow \angle PCA=\angle PAC \\\Rightarrow \triangle PAC \sim \triangle DAB (AAA) \Rightarrow \angle APC=\angle ADB，因此甲作法正確$$

$$乙的作法(見上圖)，由於\overline{CP} =\overline{CD} \Rightarrow \angle CPD=\angle CDP；\\由於\angle APC+ \angle CPD=180^\circ = \angle ADB +\angle CDP，因此\angle APC= \angle ADB，乙作法也正確；\\故選\bbox[red, 2pt]{(A)}$$

解答：

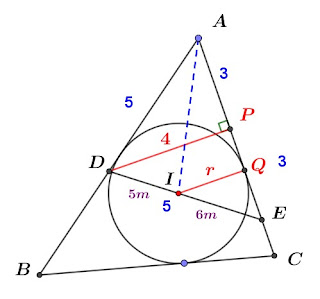
$$\overline{DE}= \overline{AD}=5 \Rightarrow \angle A=\angle DEA \Rightarrow \overline{AE} 的中垂線經過D，即 \cases{\overline{AP}=\overline{PE} = \overline{AE}\div 2=3 \\\overline{DP} \bot \overline{AE} } \\ \Rightarrow 直角\triangle APD (\angle APD=90^\circ) \Rightarrow \overline{DP}^2 =\overline{AD}^2-\overline{AP}^2 =25-9=16 \Rightarrow \overline{DP}=4\\ I是內心\Rightarrow {\overline{EI} \over \overline{ID}} ={\overline{AE} \over \overline{AD}} ={6\over 5}\Rightarrow \cases{\overline{IE}=6m\\ \overline{DI}=5m}，又\overline{IQ} \parallel \overline{DP} \Rightarrow {\overline{IQ} \over \overline{DP}}={\overline{IE} \over \overline{DE}} \\ \Rightarrow {r\over 4} ={6m\over 11m} \Rightarrow r= {24\over 11} \Rightarrow I至\overline{BC}距離=內切圓半徑r= {24\over 11}，故選\bbox[red, 2pt]{(A)}$$

解答：

(1)$$假設碳排放量為x，其標示38公克，代表 {36+38\over 2} \le x \le {38+40\over 2} ，即37\le x\le 39\\，因此\bbox[red, 2pt]{最大值為39，最小值為37}$$(2)$$減少為原本的90\% \Rightarrow 37\times 90\% \le x\times 90\%  \le 39\times 90\% \Rightarrow 33.3 \le x\times 90\%  \le 35.1 \\ \Rightarrow 碳足跡標示可能為\bbox[red, 2pt]{34或36}$$ 

解答：

(1)$$(x,y)=(縱切數,橫切數) \Rightarrow \cases{(4,0)=(0,4) \to 5塊\\ (3,1)=(1,3)\to 8塊\\ (2,2)  \to 9塊} \Rightarrow 切4刀可得蛋糕數:\bbox[red, 2pt]{5,8,9}$$(2)$$(x,y)=(縱切數,橫切數) \Rightarrow 側面不焦脆的個數=(x-1)(y-1)=60，且需符合x+y \le 20的條件；\\ \begin{array}{cc|cc|r} x-1 & y-1 & x & y &x+y\\\hline 2 & 30 & 3 & 31 &   \gt 20\\ 3 & 20 & 4 & 21 &   \gt 20 \\ 4 & 15 & 5 & 16 &   \gt 20\\ \hdashline 5 & 12 & 6 & 13 & 19 \\ 6 & 10 & 7 & 11 & 18\\ 10 & 6 & 11 & 7 & 18 \\ 12 & 5 & 13 & 6 & 19 \\\hdashline 15 & 4 & 16 & 5 &   \gt 20 \\ 20 & 3 & 21 & 4 &   \gt 20\\ 30 & 2 & 31 & 3 &  \gt 20 \\\hline\end{array}\\ 需要切\bbox[red, 2pt]{18或19}刀$$
 

=============== END =============

解題僅供參考，其它試題及詳解