111學年度學科能力測驗試題-數學B考科
一 、 單 選 題 ( 占 35 分 )
解答:$$\cases{x\ge 0 \Rightarrow 2x+x\lt 10 \Rightarrow 0\le x\lt 10/3 \Rightarrow x=0,1,2,3\\ x\lt 0 \Rightarrow -2x+x\lt 10 \Rightarrow -10\lt x\lt 0 \Rightarrow x=-1,-2,\dots,-9}\\ \Rightarrow x=-9,-8,\cdots,3,共有13個,故選\bbox[red,2pt]{(1)}$$解答:$$一次循環藍白紅白需要5+2+6+2=15秒,六次循環需要15\times 6=90,\\接著藍燈(90+5=95)、白燈(95+2=97)、紅燈(97+6=103);\\因此99-101秒之間都是亮紅燈,故選\bbox[red,2pt]{(3)}$$
解答:$$(1,4,6-8)\to 3種、(1,5,7-8)\to 2種、(1,6,8)\to 1種;\\(2,4,6-8)\to 3種、(2,5,7-8)\to 2種、(2,6,8)\to 1種;\\(4,6,8)\to 1種;共有(3+2+1)+ (3+2+1)+1=13種選法,故選\bbox[red,2pt]{(2)}$$
解答:$$ \cases{P(\log{1\over 2},2^{-5})\\ Q(x,y)} \Rightarrow \overrightarrow{PQ}=(x-\log{1\over 2},y-2^{-5})=(\log{1\over 5},-10^{-5}) \Rightarrow \cases{x-\log{1\over 2}= \log{1\over 5} \\y-2^{-5}= -10^{-5}}\\\Rightarrow \cases{x=\log{1\over 5}+ \log{1\over 2} =\log{1\over 10} \lt 0\\ y= 2^{-5}-10^{-5} \gt 0} \Rightarrow Q在第二象限,故選\bbox[red,2pt]{(2)}$$
解答:$$A=\begin{bmatrix} 1 & 1\\ 1 &-1\end{bmatrix} \Rightarrow A^2=\begin{bmatrix} 2 & 0\\ 0 &2\end{bmatrix} \Rightarrow A^6=\begin{bmatrix} 2^3 & 0\\ 0 &2^3 \end{bmatrix} =\begin{bmatrix} 8 & 0\\ 0 &8 \end{bmatrix} \Rightarrow A^7= \begin{bmatrix} 8 & 8\\ 8 & -8 \end{bmatrix}\\ \Rightarrow A^7-3A=\begin{bmatrix} 8-3 & 8-3\\ 8-3 & -8+3 \end{bmatrix} =\begin{bmatrix} 5 & 5\\ 5 & -5 \end{bmatrix} =\begin{bmatrix} a & b\\ c &d\end{bmatrix} \\ \Rightarrow a+b+c+d = 5+5+5-5=10,故選\bbox[red,2pt]{(5)}$$
解答:$$令\theta=北極至甲地的角度\Rightarrow r\theta ={7\over 12}\pi r \Rightarrow \theta ={7\over 12}\pi =105^\circ =90^\circ +15^\circ \\ \Rightarrow 甲在南緯15^\circ,故選\bbox[red,2pt]{(3)}$$
解答:$$\overline{Q_1Q_2} =\overline{Q_2Q_3} =\overline{Q_3Q_4} \Rightarrow \cases{Q_1=a\\ Q_2= a+d\\ Q_3=a+2d\\ Q_4=a+3d} \Rightarrow K={ \overline{Q_1Q_4}\times \overline{Q_2Q_3} \over \overline{Q_1Q_3}\times \overline{Q_2Q_4}} ={3d\times d\over 2d\times 2d} ={3\over 4}\\(1) K={7\times 2\over 3\times 5} \ne {3\over 4}\\ (2) K={6\times 2\over 3\times 5} \ne {3\over 4} \\(3)K= {8\times 3\over 7\times 4} \ne {3\over 4} \\(4)K= {8\times 2\over 2\times 7} \ne {3\over 4} \\(5) K={9\times 2\over 8\times 3} = {3\over 4}\\,故選\bbox[red,2pt]{(5)}$$
二、多選題(占25分)
解答:$$(1)\bigcirc: 原點(0,0)至(1,a)的直線斜率={a-0\over 1-0}=a\\(2)\bigcirc: 圓心(4,6)至原點直線的斜率={6\over 4}={3\over 2}=a,剛好射中圓心 \\(3)\times: \cases{d_1=d((2,2),y=ax)=(2a-2)/\sqrt{a^2+1}\\d_2=d((8,1),y=ax)=(8a-1)/\sqrt{a^2+1}} \Rightarrow d_1^2+d_2^2 ={68a^2-24a+5\over a^2+1} \gt 2\\(4)\times:圓心(2,2)至直線y={3\over 2}x的距離= {6-4\over \sqrt{3^2+(-2)^2}} ={2\over \sqrt{13}} \lt 1 \Rightarrow a=3/2可以射中(2,2)及(4,6)兩個圓盤\\\qquad 但(8,1)至直線y={3\over 2}x的距離={21\over \sqrt{13}} \gt 1,無法射中(8,1)圓盤\\(5)\bigcirc: (8,1)至直線y={16\over 63}x的距離={128-63\over \sqrt{16^2+63^2}}=1\\,故選\bbox[red,2pt]{(1,2,5)}$$解答:$$(1)\bigcirc: f(1)=2-3+1=0 \Rightarrow 圖形通過(1,0)\\(2)\times f'(x)=0 \Rightarrow 6x^2-3=0 \Rightarrow x=\pm {1\over \sqrt 2} \Rightarrow \cases{f(1/\sqrt 2)=1-\sqrt 2\lt 0\\ f(-1/\sqrt 2)=1+\sqrt 2 \gt 0}\Rightarrow 有三相異實根\\(3) \times: f''(x)=12x=0 \Rightarrow x=0 \Rightarrow 對稱中心(0,f(0))=(0,1) \ne (1,0)\\(4)\times: f'(0)=-3 \Rightarrow y=-3(x-0)+1 \Rightarrow 3x+y=1 \\(5)\times: 兩函數最高項係數分別為2及3,無法僅靠平移達成\\,故選\bbox[red,2pt]{(1)}$$
解答:$$(1)\bigcirc: 0\le x_1\le 100 \Rightarrow 0.8x_1+20-x_1=20-0.2x_1 \ge 0 \Rightarrow 調整後\ge 調整前\\(2) \bigcirc: E(y_1)= E(y_2)=60 \Rightarrow \cases{E(0.8x_1+20)= 0.8E(x_1)+20=60\\ E(0.75x_2+25) =0.75E(x_2)+25=60} \Rightarrow \cases{E(x_1)=50\\ E(x_2)= 140/3}\\ \qquad \Rightarrow E(x_1)\gt E(x_2)\\(3) \times: \cases{\sigma(y_1)=16 \\\sigma(y_2)= 15} \Rightarrow \cases{\sigma(0.8x_1+20)= 0.8\sigma(x_1)=16\\ \sigma(0.75x_2+25)=0.75\sigma(x_2)=15} \Rightarrow \cases{\sigma(x_1)=20 \\ \sigma(x_2)=20} \Rightarrow \sigma(x_1)= \sigma(x_2)\\(4)\bigcirc:0.8x_1+20 \gt 0.75x_2+25 \Rightarrow 0.75(x_1-x_2)+0.05x_1\gt 5 \Rightarrow x_1-x_2\gt 0 \Rightarrow x_1\gt x_2 \\(5)\times:(0.75x+25)-(0.8x+20)= 5-0.05x \ge 0, x\in [0,100] \Rightarrow 乙班調整幅度較大;\\\qquad 所以乙班調分前不及格人數可能較甲班多\\,故選\bbox[red,2pt]{(124)}$$
解答:
$$同時滿足\vec v\cdot \overrightarrow{OA} \gt 0 且\vec v\cdot \overrightarrow{OB} \gt 0,表示\vec v與此二向量夾角小於90^\circ;\\在此條件下,再試求與其他向量夾角是否大於90^\circ;\\由上圖可知,\overrightarrow{OD}、\overrightarrow{OE}兩向量與\vec v 內積一定為負值,故選\bbox[red,2pt]{(23)}$$
解答:$$(1)\times: 1\le x-2\le 3 \Rightarrow 3\le x\le 5\\(2)\times:1\le x+2 \le 3 \Rightarrow -1\le x\le 1 \\(3) \bigcirc: 1\le 2x-7 \le 3 \Rightarrow 4 \le x\le 5\\(4)\times: 1\le {x+7\over 2}\le 3 \Rightarrow -5\le x\le -1 \\(5) \bigcirc: 1\le 3x-11\le 3 \Rightarrow 4 \le x\le 14/3\lt 5\\,故選\bbox[red,2pt]{(35)}$$
三、選填題(占 2 5 分 )
解答:$$2\log y=1 \Rightarrow y^2=10 \Rightarrow y=\sqrt{10} \Rightarrow x^{-1/3}y^2= x^{-1/3}\cdot 10=1 \Rightarrow {1\over \sqrt[3]{x}} ={1\over 10} \\ \Rightarrow x=10^3 \Rightarrow {x-y^2\over 10}={10^3-10\over 10}=10^2-1= \bbox[red,2pt]{99}$$解答:
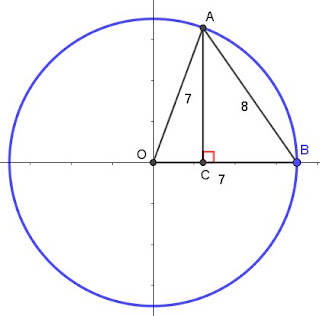
$$\cos \angle AOB={7^2+7^2-8^2\over 2\cdot 7\cdot 7} ={17\over 49} \Rightarrow \overrightarrow{OA}\cdot \overrightarrow{OB} = \overline{OA}\cdot \overline{OB}\cos \angle AOB =7\times 7\times {17\over 49} =\bbox[red,2pt]{17 }$$
解答:$${有裝傳送器且被找到 \over 有裝傳送器且被找到+ 有裝傳送器且沒被找到} ={70\%\times 60\%\over 70\%\times 60\% +30\%\times 10\%} ={0.42\over 0.45} =\bbox[red,2pt]{14\over 15}$$
解答:$$假設\cases{藍球有b個\\ 綠球有g個} \Rightarrow \cases{C^b_2/C^{10}_2 =1/15 \Rightarrow b=3\\ C^g_2/C^{10}_2 =2/9 \Rightarrow g=5} \Rightarrow 黃球有y=10-5-3=2個\\ 抽中兩球為異色的機率:\cases{P(1藍1綠)=C^3_1C^5_1/C^{10}_2 \\ P(1藍1黃)=C^3_1C^2_1/C^{10}_2 \\P(1綠1黃)=C^5_1C^2_1/C^{10}_2 } \Rightarrow 機率相加={15+6+10\over 45}= \bbox[red,2pt]{31\over 45}$$
解答:$$6位同學任排,有6!=720種排法\\、不愉快的男女排在一起有8種排法(兩人在12、23 、56、67,再左右互換,老師固定在4)\\剩下4人任排有4!排法 、左邊全是男生或全是女生有2種情形,每一種有3!\times 3!排法\\,因此符合要求的有720-8\times 4!-2\times 3!\times 3!= \bbox[red,2pt]{456}種$$
解答:$$假設\cases{藍球有b個\\ 綠球有g個} \Rightarrow \cases{C^b_2/C^{10}_2 =1/15 \Rightarrow b=3\\ C^g_2/C^{10}_2 =2/9 \Rightarrow g=5} \Rightarrow 黃球有y=10-5-3=2個\\ 抽中兩球為異色的機率:\cases{P(1藍1綠)=C^3_1C^5_1/C^{10}_2 \\ P(1藍1黃)=C^3_1C^2_1/C^{10}_2 \\P(1綠1黃)=C^5_1C^2_1/C^{10}_2 } \Rightarrow 機率相加={15+6+10\over 45}= \bbox[red,2pt]{31\over 45}$$
解答:$$6位同學任排,有6!=720種排法\\、不愉快的男女排在一起有8種排法(兩人在12、23 、56、67,再左右互換,老師固定在4)\\剩下4人任排有4!排法 、左邊全是男生或全是女生有2種情形,每一種有3!\times 3!排法\\,因此符合要求的有720-8\times 4!-2\times 3!\times 3!= \bbox[red,2pt]{456}種$$
第貳部分、混合題或非選擇題(占15分)
解答:$$18\times {\pi\over 180}={\pi\over 10},故選\bbox[red,2pt]{(4)}$$
解答:$$\sin \theta ={偏移距離\over 塔高} \Rightarrow \cases{\sin \theta_1=2.3/48\approx 0.05\\ \sin \theta_2=2.3/19 =6.9/57\\ \sin \theta_3= 4/57\approx 0.07 } \Rightarrow \bbox[red,2pt]{\theta_2\gt \theta_3\gt \theta_1}$$
解答:$$假設塔高a,則a\sin \beta-a\sin \alpha= a({7\over 25}-{1\over 5})= a\cdot {2\over 25}=20 \Rightarrow a=250\\又\cases{\sin \alpha=1/5\\ \sin \beta=7/25} \Rightarrow \cases{\cos \alpha=2\sqrt 6/5 \\ \cos \beta= 24/25} \Rightarrow a\cos \alpha-a\cos \beta =250({2\sqrt 6\over 5}-{24\over 25})=\bbox[red,2pt]{100\sqrt 6-240}$$
======================== END =============================
解題僅供參考,其他學測試題及詳解























感謝朱老師的分享
回覆刪除