111 年度自學進修普通型高級中等學校畢業程度學力鑑定考試試卷
科目： 數學
一、 選擇題：（ 12 題，每題 5 分，共 60 分）
解答：$$-8\le x\le 4 \Rightarrow -6\le x+2\le 6 \Rightarrow |x+2|\le 6 \Rightarrow a=6，故選\bbox[red, 2pt]{(A)}$$
解答：$$(x^2+4x+4)+(y^2+6y+9)+k =13 \Rightarrow (x+2)^2 +(y+3)^2 =13-k\gt 0 \\\Rightarrow k=12 符合條件，故選\bbox[red, 2pt]{(D)}$$
解答：$$由圖形可知:\cases{m_1\lt 0\\ m_2\lt 0\\ m_3 \gt 0\\ m_4=0}且m_1\gt m_2，故選\bbox[red, 2pt]{(B)}$$
解答：$$\cases{a_2 =6\\ a_4 =a_2r^2=54} \Rightarrow {a_2\over a_2r^2}={6\over 54} \Rightarrow {1\over r^2}={1\over 9} \Rightarrow r=-3 \Rightarrow a_2= a_1r=-3a_1= 6 \Rightarrow a_1=-2\\ \Rightarrow a_1+a_2+\cdots +a_5= a_1(1+r+\cdots+ r^4) =(-2)\times {1-(-3)^5\over 1-(-3)} =(-2)\times {1+243\over 4}\\ =-122，故選\bbox[red, 2pt]{(A)}$$
解答：$$x越大而y越小，則相關係數為負值，故選\bbox[red, 2pt]{(B)}$$
解答：$$出現偶數與出現奇數的機率均為{1\over 2}，因此丟一次骰子的期望值{1\over 2}(5+1)=3 \\\Rightarrow 擲三次期望值=3\times 3=9，故選\bbox[red, 2pt]{(B)}$$
解答：$$正弦定理:{ \overline{BC}\over \sin A} ={ \overline{AC}\over \sin B} ={ \overline{AB}\over \sin C} \Rightarrow { \overline{BC}\over 8} ={ \overline{AC} \over 15} ={ \overline{AB}\over 17} \\\Rightarrow \overline{BC}: \overline{AC}:\overline{AB} =8:15:17，而17^2=8^2+15^2，因此\angle C=90^\circ，故選\bbox[red, 2pt]{(D)}$$
解答：$$\log a=\log b+2 =\log b+\log 100=\log 100b \Rightarrow a=100b，故選\bbox[red, 2pt]{(D)}$$
解答：$$\vec a\bot \vec b \Rightarrow \vec a\cdot \vec b=0 \Rightarrow (t-1,2t+3) \cdot (1,2)= t-1+4t+6=0 \Rightarrow 5t+5=0 \Rightarrow t=-1\\，故選\bbox[red, 2pt]{(A)}$$
解答：$$\cases{A={1\over 2}((A+B)+(A-B)) ={1\over 2}\begin{bmatrix}3+1 & 5-1\\ 4-2& 3+5 \end{bmatrix} =\begin{bmatrix}2 & 2\\ 1& 4 \end{bmatrix} \\[1ex] B={1\over 2}((A+B)-(A-B)) ={1\over 2}\begin{bmatrix}3-1 & 5+1\\ 4+2& 3-5 \end{bmatrix} =\begin{bmatrix} 1 & 3\\ 3& -1 \end{bmatrix}} \\ \Rightarrow \cases{A^2= \begin{bmatrix} 6 & 12\\ 6 & 18 \end{bmatrix} \\[1ex] B^2= \begin{bmatrix} 10 & 0\\0 & 10 \end{bmatrix}} \Rightarrow A^2-B^2 =\begin{bmatrix} -4 & 12\\ 6& 8 \end{bmatrix}，故選\bbox[red, 2pt]{(C)}$$
解答：$$(A)\times: \overline{AD}\bot \overline{CD}\\ (B)\times: \overline{AD}與\overline{DE}相交\\ (D)\times: \overline{AD}\parallel \overline{BC}\\，故選\bbox[red, 2pt]{(C)}$$
解答：$$R\cos n^\circ =r \Rightarrow \cos n^\circ={r\over R}= {1\over 2} \Rightarrow n=60，故選\bbox[red, 2pt]{(C)}$$
二、填充題：（ 10 題，每題 4 分，共 40 分）
解答：$$算幾不等式:{a+2b\over 2}\ge \sqrt{a\cdot 2b} \Rightarrow a+2b\ge 2 \sqrt{2\cdot 32} =16 \Rightarrow a+2b的最小值為\bbox[red,2pt]{16}$$
解答：$$\cases{L_1斜率m_1= -2/3\\ L_2斜率m_2= 3/k} \Rightarrow m_1\times m_2=-1 \Rightarrow -{2\over k}=-1 \Rightarrow k=\bbox[red, 2pt] 2$$
解答：$$f(1)=4 \Rightarrow 1+a-5-1=4 \Rightarrow a=\bbox[red,2pt]9$$
解答：$$\cases{(x-10)^2 \ge 0\\ x^2+x+1=(x+{1\over 2})^2+{3\over 4}\gt 0} \Rightarrow (x-10)^2 (x^2+x-6)(x^2+x+1)\lt 0 \\ \Rightarrow x^2+x-6\lt 0 \Rightarrow (x+3)(x-2)\lt 0 \Rightarrow -3\lt x\lt 2 \Rightarrow x=-2,-1,0,1\\ \Rightarrow 共有\bbox[red, 2pt] 4個整數解$$
解答：$$第一個有C^4_1=4種選擇、最後一個有C^3_1=3種選擇、剩下4人任排有4!排法\\，因此共有4\times 3\times 4!= \bbox[red, 2pt]{288}種$$
解答：$$r\theta =3\times 2= \bbox[red, 2pt]{6}$$
解答：$$圖形經過三點:\cases{(0,8)\\ (1,4)\\ (2,2)} \Rightarrow \cases{8=k\times a^0=k\\ 4=k\times a^1=ak\\ 2=k\times a^2} \Rightarrow \cases{k=8\\ a=4/8=1/2} \Rightarrow (k,a)=\bbox[red,2pt]{(8,1/2)}$$
解答：$$令\cases{\overline{AE} =a\\ \overline{AB}=b\\ \overline{AD}= c} \Rightarrow \cases{a^2+b^2 =(2\sqrt 5)^2=20\\ b^2+c^2 = (\sqrt{13})^2 =13\\ a^2+c^2 = 5^2=25} \Rightarrow \cases{a^2=16\\ b^2=4\\ c^2=9} \\ \Rightarrow 長方體體積=\sqrt{a^2b^2c^2} =\sqrt{16\cdot 4\cdot 9} =4\cdot 2\cdot 3=\bbox[red, 2pt]{24}$$
解答：$$\cases{a+b=35\\ a+c=30\\ a+b+c+7=50} \Rightarrow \cases{a=22\\ b=13\\c=8} \Rightarrow 女生選墾丁的機率={b\over b+7} =\bbox[red, 2pt]{13\over 20}$$
解答：$${第一型用甲藥治癒\over 第一型用甲藥治癒+第二型用甲藥治癒} ={70\%\times 80\% \over 70\%\times 80\% +30\%\times 40\%} ={56\% \over 56\%12\%} = \bbox[red,2pt]{14\over 17}$$
========================== END ============================
解題僅供參考，其他學力鑑定試題及詳解
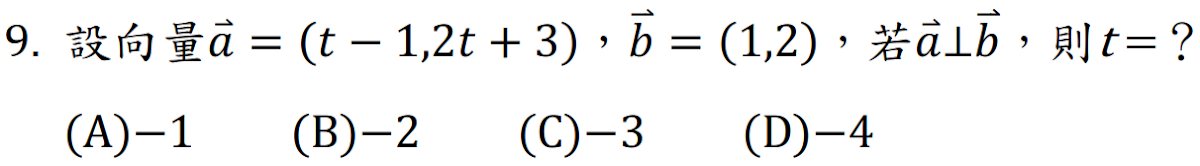
沒有留言:
張貼留言