103年國中會考數學詳解

試題來源:師大心測中心
第一部分：選擇題(1~27)

解：

$$\left( \sqrt { 6 } +\sqrt { 10 } \times \sqrt { 15 }  \right) \times \sqrt { 3 } =\sqrt { 6\times 3 } +\sqrt { 10\times 15\times 3 } =\sqrt { 18 } +\sqrt { 450 } \\ =3\sqrt { 2 } +15\sqrt { 2 } =18\sqrt { 2 }$$ 

故選(D)。

---

解：$$A=2^{ 5 }\times 7^{ 6 }\times 11^{ 4 }=\left( 2^{ 4 }\times 7^{ 4 }\times 11^{ 4 } \right) \times \left( 2\times 7^{ 2 } \right) $$

故選(C)。

---

解：

$$在直角\triangle ABE\Rightarrow { \overline { AE }  }^{ 2 }={ \overline { AB }  }^{ 2 }-{ \overline { BE }  }^{ 2 }=10^{ 2 }-8^{ 2 }=6^{ 2 }\Rightarrow \overline { AE } =6\\ 在直角\triangle ADE\Rightarrow { \overline { AD }  }^{ 2 }={ \overline { DE }  }^{ 2 }-{ \overline { AE }  }^{ 2 }=\left( 6\sqrt { 3 }  \right) ^{ 2 }-6^{ 2 }=72\Rightarrow \overline { AD } =6\sqrt { 2 } $$

故選(C)。

---

解：

取出不放回，共有3×2=6種情形，只有54是6的倍數，因此機率為1/6，故選(A)。

---

解：

原式=(741+2)(370-1)-741×370=741×370-741+2×370-2-741×370

=-741+2×370-2=740-741-2=-3

故選(A)。

也就是令\(y=370,x=741=2y+1\), 則原式為\((x+2)(y-1)-xy=-x+2y-2=-(2y+1)+2y-2=\bbox[red,2pt]{-3}\)

---

解：$$\begin{cases}5x-y=5\cdots(1)\\y=\frac{1}{5}x\cdots(2)\end{cases}\Rightarrow \text{由(2)可知 }x=5y\text{ 代入(1)可得 }25y-y=5\Rightarrow y=\frac{5}{24}\\ \Rightarrow a+b=x+y=5y+y=6y=6\times\frac{5}{24}=\frac{5}{4},故選\bbox[red,2pt]{(A)}$$

---

解：

0.5公斤的番茄要10元⇒1公斤的番茄要20元⇒250元的番茄重250/20=12.5公斤⇒空竹籃=15-12.5=2.5公斤

故選(C)。

---

解：

選(A)可拼湊成下圖

上圖與紅線對稱，故選(A)。

---

解：

F到y軸的直線為紅線(如下圖)，由於兩三角形全等，所以兩條紅線長度相等。又三角形BAC為等腰，所以紅線與藍線長度相等。藍線長度=A點y座標-C點y座標=1-(-3)=4。

故選(C)。

---

解：

$$\angle A=180^\circ-\angle B-\angle C=180^\circ-74^\circ-46^\circ=60^\circ\Rightarrow \overset{\large{\frown}}{BC}=120^\circ\Rightarrow \overset{\large{\frown}}{FC}=60^\circ\\ \triangle GEC\Rightarrow \angle GEC=180^\circ-90^\circ-46^\circ=44^\circ =\frac{\overset{\large{\frown}}{FC}+\overset{\large{\frown}}{AD}}{2}= \frac{60^\circ+\overset{\large{\frown}}{AD}}{2}\Rightarrow \overset{\large{\frown}}{AD}=28^\circ ,\\故選\bbox[red,2pt]{(B)}$$

---

解：

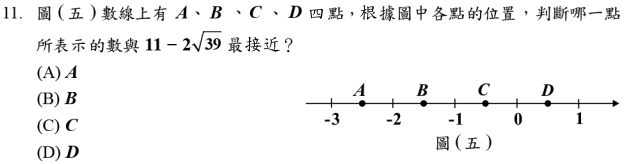
由以上計算可知\(\sqrt{39}=6.24\Rightarrow 11-2\sqrt{39}=11-12.48=-1.48\)

如果你不會手算開根號，只好這樣算:

\(6.5^2=42.25>39\Rightarrow 6<\sqrt{39}<6.5\Rightarrow 12<2\sqrt{39}<13\Rightarrow -2<11-2\sqrt{39}<-1,故選\bbox[red,2pt]{(B)}\)

---

解：$$\frac{\triangle ADC}{\triangle AGC}=\frac{\overline{CD}}{\overline{CG}}=\frac{\overline{CF}}{\overline{FB}}=\frac{6}{6+9}= \frac{2}{5} \Rightarrow \triangle ADC=\frac{2}{5}\triangle AGC\Rightarrow \triangle AGD=\frac{3}{5}\triangle AGC\\ \Rightarrow \frac{\triangle ADC}{\triangle AGD}=\frac{2/5\times\triangle AGC}{3/5\times\triangle AGC}=\frac{2}{3};\\又\triangle AGD=\frac{1}{2}\overline{AG}\times\overline{BF}=\frac{1}{2}\times 8\times 9=36\Rightarrow \triangle ADC=\frac{2}{3}\times 36=24,故選\bbox[red,2pt]{(B)}.$$

---

解：

將公車位置視為原點，上方為北方，可得以下平面座標圖

因此，從郵局到小杰家=(400,-300)→(300,400)，需向北走400公尺再向西走100公尺，故選(A)。

---

解：

1.36×10¹⁸×0.3×10^-2=0.408×10¹⁶=4.08×10¹⁵

故選(B)。

---

解：

除式為2次式，餘式為1次式，因此只有(C)及(D)符合要求；又除式沒有常數項，因此餘式的常數項就是被除式的常數項，即-5，故選(D)。

---

解：

令\(\overline{EG}=\overline{AC}=a\), 則\(\overline{CE}= \overline{AG}-\overline{EG}-\overline{AC}=2-2a\)。

因此\(\overline{OC}= \overline{OG}+\overline{GE} +\overline{CE}=1+a+2-2a=3-a\)、\(\overline{OE}=a+1\)

\(\Rightarrow \overline{OC}+\overline{OE}=3-a+a+1=4\)

\(\overset{\large{\frown}}{CD}+\overset{\large{\frown}}{EF}=(\overline{OC}+ \overline{OE})\times \frac{\pi}{3}=\frac{4\pi}{3}，故選\bbox[red,2pt]{(B)}\)。

---

17. (3x+2)(-x⁶+3x⁵)+(3x+2)(-2x⁶+x⁵)+(x+1)(3x⁶-4x⁵)與下列哪一個式子相同？

(A)(3x⁶-4x⁵)(2x+1)

(B)(3x⁶-4x⁵)(2x+3)

(C)-(3x⁶-4x⁵)(2x+1)

(D)-(3x⁶-4x⁵)(2x+3)

解：

原式=(3x+2)(-x⁶+3x⁵-2x⁶+x⁵⁾+(x+1)(3x⁶-4x⁵) 

=(3x+2)(-3x⁶+4x⁵)+(x+1)(3x⁶-4x⁵)

=-(3x+2)(3x⁶-4x⁵)+(x+1)(3x⁶-4x⁵)

=(3x⁶-4x⁵)(-3x-2+x+1)=(3x⁶-4x⁵)(-2x-1)=-(3x⁶-4x⁵)(2x+1)

故選(C)。

---

解：

M為角平分線⇒∠ABP=∠PBC

L為中垂線⇒∠PBC=∠PCB

60+24+3a=180⇒a=32

故選(C)。

---

解：

原有水量: 甲=60×10=600、乙=80×10=800、丙=100×10=1000

現將甲杯的a立方公分及乙杯的b立方公分加入丙杯

⇒甲=600-a、乙=800-b、丙=1000+a+b

⇒甲高度=(600-a)/60、乙高度=(800-b)/80、丙高度=(1000+a+b)/100

⇒(600-a)/60:(800-b)/80:(1000+a+b)/100=3:4:5

⇒a=168, b=32⇒甲高度=(600-168)/60=7.2

故選(C)。

---

解：

故選(D)。

---

解：

故選(D)。

---

解：

假設共有a人在KTV歡唱6小時

包廂方案: 900×6+99×a元

人數方案：540×a+3×80×a=780a元

 900×6+99a<780a⇒5400<681a⇒7.9<a，故選(C)。

---

解：

令首項為a, 公差為d

前9項和=(a+a+8d)×9/2=54⇒a+4d=6----(1)

第1、4、7項的和=a+(a+3d)+(a+6d)=36⇒a+3d=12---(2)

(1)-(2)⇒d=-6，故選(A)。

---

解：

(C) 與 (D) 皆可能如上圖，皆不是平行四邊形

(A)由於相鄰相邊不垂直，所以右邊的藍線長度也可以是5

故選(B)。

---

解：

將乙箱內的球依號碼從小排到大，第25顆球的號碼為40。

乙箱中有24顆球的號碼小於40，也有24顆球的號碼大於40。

原來甲箱中有1~39顆球的號碼小於40，後來剩下39-24=15顆球的號碼小於40；原來甲箱中有41~98顆球的號碼大於40，後來剩下58-24=34顆球的號碼大於40。因此a=15, b=34，故選(D)。

---

解：

由a<0可知抛物線有極大值；又A點較B點為高，所以頂點(h, k)較接近A點，即h離10比較近，離0比較遠。所以h會在0與10的中間(5)偏右，故選(D)。

---

解：

甲乙皆錯誤，故選(B)。

---

解：

甲校男生數=(60/100)×a、乙校男生數=(50/100)×b，

合併後的男生數=(60/100)×a+(50/100)×b，故合併後的比率為[(60/100)×a+(50/100)×b]/(a+b)。

小清的答案不一定正確，若要正確必須

[(60/100)×a+(50/100)×b]/(a+b)=55/100

⇒(0.6a+0.5b)/(a+b)=0.55⇒a=b

只有在甲乙兩校有相同的人數，小清的答案才會正確。

---

證：

由題意知：∠1+∠2=∠3+∠4=∠4+∠5=90。

其中∠3+∠4=∠4+∠5⇒∠3=∠5

又∠1+∠2+∠3+∠4=180⇒180-(∠1+∠3)=∠2+∠4

⇒∠B=∠2+∠4⇒∠B=∠7

由∠3=∠5、BC=CE、∠B=∠7可知兩三角形符合全等條件ASA，所以△ABC與△DEC全等。

---

--- END ---