1. 算式 -6+2×[16-(-32)÷8] 之值為何?
(A) -24 (B) -4 (C) 30 (D) 3
解:
$$-6+2\times [16-(-32)\div 8]=-6+2\times [16-(-4)]\\ =-6+2\times [16+4]=-6+2\times [20]\\ =-6+40=34$$
故選(D)。
------------------------------------------------
2. 數線上A、B兩點所表示的數分別為a、b,且a<b, |a-b|=9。若從A點向右移動3單位到達C點,則B、C兩點的距離為何?
(A)3 (B) 6 (C) 9 (D) 12
解:a<b => B在A的右邊
|a-b|=9 => A、B的距離為9
A點向右移動3單位 => 此時A、B的距離為6
故選 (B)。
------------------------------------------------
3. 有一座水池內部呈長方體,水深為500公分。小明想要將水池內的水,以每30分鐘下降40公分的速率,等速放水5小時。若經過x分鐘後,水深為y公分,則下列哪一個圖形可以表示x、y的關係?
解:
30分鐘下降40公分 => y軸/x軸 = 40/30 , 故選 (B)。
------------------------------------------------4. 圖(一)中,四邊形ABCD為平行四邊形,四邊形ACDE為菱形。若∠1為∠BCD的外角,則下列有關∠1、∠ADE、∠ACB的大小關係,何者正確?
(A) ∠ADE>∠1 (B) ∠ADE<∠1
(C) ∠ACB<∠1 (D) ∠ACB=∠1
解:
假設∠EDA=∠2, ∠CDB=∠3 且 ∠ADB=∠4
ED//AC 且 AD//BC => ∠DAC=∠ACB =∠2
又AD//BC => ∠ADB=∠DBC=∠4
四邊形ACDE為菱形 => ∠2=∠3+∠4
因此∠ACB=∠2=∠3+∠4=∠1,故選(D)。
------------------------------------------------
5. 如圖(二),三直線圍成一個三邊圴不等長的銳角三角形ABC。根據圖中各角度的位置,判斷下列關係何者正確?
(A) ∠1+∠3 >90 (B)∠3+∠5<90
(C)∠4=∠1+∠2 (D)∠5=∠1+∠3
解:
銳角三角形任一內角均小於90,也代表任兩內角和大於90,故選(A)。
------------------------------------------------
解:
$$\frac { 3A+B }{ 2 } -\frac { A-3B }{ 3 } =\frac { 3(3A+B) }{ 6 } -\frac { 2(A-3B) }{ 6 } \\ =\frac { 9A+3B }{ 6 } -\frac { 2A-6B }{ 6 } =\frac { 9A+3B-(2A-6B) }{ 6 } \\ =\frac { 9A+3B-2A+6B }{ 6 } =\frac { 7A+9B }{ 6 } \\ =\frac { 7(2x-3)+9(3x+1) }{ 6 } =\frac { 14x-21+27x+9 }{ 6 } \\ =\frac { 41x-12 }{ 6 } $$
故選(B)。
------------------------------------------------
7. 在30~50的正整數中,將與48互質的數由小到大排列,則第5個數為何?
(A) 37 (B) 41 (C) 43 (D) 47
解:
48的質因數為2與3,與48互質的數不能有2或3的倍數。
30=2×15, 31, 32=2×16, 33=3×11, 34=2×17, 35, 36=2×18, 37, 38=2×19, 39=3×13, 40=2×20, 41, 42=2×21, 43, 44=2×22, 45=3×15, 46=2×23, 47, 48=2×24....
與48互質的數=> 31, 35, 37, 41, 43, 47, .....
第5個是43,故選(C)。
------------------------------------------------
解:
$$\frac { 6 }{ \sqrt { 7 } -\sqrt { 5 } } -\frac { 12 }{ \sqrt { 11 } +\sqrt { 5 } } \\ =\frac { 6(\sqrt { 7 } +\sqrt { 5 } ) }{ (\sqrt { 7 } -\sqrt { 5 } )(\sqrt { 7 } +\sqrt { 5 } ) } -\frac { 12(\sqrt { 11 } -\sqrt { 5 } ) }{ (\sqrt { 11 } +\sqrt { 5 } )(\sqrt { 11 } -\sqrt { 5 } ) } \\ =\frac { 6(\sqrt { 7 } +\sqrt { 5 } ) }{ 2 } -\frac { 12(\sqrt { 11 } -\sqrt { 5 } ) }{ 6 } =3(\sqrt { 7 } +\sqrt { 5 } )-2(\sqrt { 11 } -\sqrt { 5 } )\\ =3\sqrt { 7 } +5\sqrt { 5 } -2\sqrt { 11 } $$
故選(D)。
------------------------------------------------
9. 已知一等差數列的公差是2,前20項和是500,求此等差數列的首項為何?
(A) 5 (B) 6 (C) 10 (D) 12
解:
令首項為a,公差為d=2
$${ S }_{ 20 }=\frac { { { a }_{ 1 }+{ a }_{ 20 } } }{ 2 } \times 20=10\left\{ a+\left( a+19d \right) \right\} \\ =10\left\{ a+\left( a+19\times 2 \right) \right\} =10\times \left( 2a+38 \right) =500\\ \Rightarrow 2a+38=50\Rightarrow 2a=12\Rightarrow a=6$$
故選(B)。
------------------------------------------------
解:
由上圖可知:圖形(A)找不到對稱軸,故選(A)。
△EFC為直角三角形,所以EF2=302+402⇒EF=50,故選(C)。
$$\frac { \overline { BP } }{ \overline { BQ } } =\frac { \overline { MN } }{ \overline { CA } } \Rightarrow \frac { \frac { 12 }{ 5 } -h }{ \frac { 12 }{ 5 } } =\frac { \overline { MN } }{ 5 } \\ \Rightarrow 12-5h=\frac { 12 }{ 5 } \times \overline { MN } \Rightarrow \overline { MN } =5-\frac { 25 }{ 12 } h$$

由於∠EOB=∠OFC=90°, 且∠B=∠C(△ABC為等腰), 因此兩三角形符合AAA,又OE=OF=3(半徑),所以△EOB與△OFC全等(ASA)。
由上圖可知:圖形(A)找不到對稱軸,故選(A)。
------------------------------------------------
解:
△ABC為等腰 ⇒ ∠B=∠C=55°, ∠A=180-55-55=70°⇒BC>AC
⇒BC-1>AC-1⇒DC>EC,故選(B)。
------------------------------------------------
12. 已知在KTV唱歌消費,除了唱歌的費用外,還需多付10%的服務費。若小明在KTV唱歌,含服務費共花了x元,則他付的服務費可用下列哪一個式子表示?
$$(A)\frac { 1 }{ 10 } x\quad \quad (B)\frac { 9 }{ 10 } x\quad \quad (C)\frac { 1 }{ 11 } x\quad \quad (D)\frac { 9 }{ 11 } x$$
解:
假設唱歌的費用為a元,則服務費為a/10元,共花了a+a/10=x
$$a+\frac { a }{ 10 } =x\Rightarrow \frac { 11a }{ 10 } =x\Rightarrow a=\frac { 10 }{ 11 } x\\ \Rightarrow \frac { a }{ 10 } =\frac { 1 }{ 11 } x$$
故選(C)。
------------------------------------------------
13. 座標平面上有一矩形ABCD,其中直線AC的方程式為x+2y=7。若B點座標為(1,1),且AB與y軸平行,則D點座標為何?
(A) (1,3) (B) (3,5) (C) (5,1) (D) (5,3)
解:
AB與y軸平行⇒AB的方程式為x=1
令A點座標為(1,a),由AC的方程式可知1+2a=7⇒a=3,即A=(1,3)。
ABCD為矩形⇒AB垂直BC⇒BC與x軸平行⇒BC的方程式為y=1
令C點座標為(c,1),代入AC方程式⇒c+2=7⇒c=5⇒C點座標為(5,1)
由A、C兩點的座標可得知D點座標為(5,3),故選(D)。
------------------------------------------------
14. 算式2×(20002-1)-20012-19992之值為何?
(A) 4 (B) -4 (C) 7998 (D) -8002
解:
$$2\times \left( { 2000 }^{ 2 }-1 \right) -{ 2001 }^{ 2 }-{ 1999 }^{ 2 }\\ =2\times \left( { 2000 }+1 \right) \left( 2000-1 \right) -{ 2001 }^{ 2 }-{ 1999 }^{ 2 }\\ =2\times 2001\times 1999-{ 2001 }^{ 2 }-{ 1999 }^{ 2 }\\ =-\left( { 2001 }^{ 2 }-{ 2\times 2001\times 1999+1999 }^{ 2 } \right) \\ =-{ \left( 2001-1999 \right) }^{ 2 }=-{ 2 }^{ 2 }=-4$$
故選(B)。
------------------------------------------------
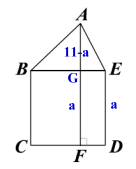
15. 圖(五)的五邊形ABCDE是由△ABE與正方形BCDE所組成,F點在CD上,且AF⊥CD。若五邊形ABCDE的面積為63,且AF=11,則△ABE與正方形BCDE的面積比為何?
(A) 2:7 (B) 3:5 (C) 3:16 (D) 5:12
解:
假設AF與BE的交點為G,且令正方形邊長為a,如下圖:
ABCDE的面積=△ABE+正方形BCDE =(11-a)a/2 +a×a=63,即
$$\frac { a\left( 11-a \right) }{ 2 } +{ a }^{ 2 }=63\Rightarrow { a }^{ 2 }+11a-126=0\\ \Rightarrow (a-7)(a+18)=0\Rightarrow a=7$$
△ABE與正方形BCDE的面積比=(11-a)a/2 : a×a = 4×7/2 :7×7
= 2:7, 故選(A)。
------------------------------------------------
------------------------------------------------
17. 如圖(六),正方形廣場ABCD的邊長為100公尺。甲、乙兩機器人均從A點同時出發,甲沿著AB與BC走至C點,乙沿著AD與DC走至C點。若甲、乙的速率分別為每分鐘16公尺、17公尺,則出發後10分鐘,此時甲、乙的位置相距多少公尺?
(A) 30 (B) 40 (C) 50 (D) 70
解:
------------------------------------------------
以BG當底邊,求取其高為h,如下圖
則平行四邊形的面積=BG×h,而△BGC面積=BG×h/2,所以△BGC面積=平行四邊形面積的一半=12/2=6;
由於G為重心,△ABC面積=3×△BGC面積=3×6=18,故選(D)。
------------------------------------------------
19. 已知有甲、乙、丙、丁四支棒球隊,每隊均與其他三隊各比20場。表(一)為四隊比賽戰積紀錄表,其中部分資料污損。根據表中的資料,判斷乙隊的獲勝場數為何?
(A) 23 (B) 24 (C) 25 (D) 26
解:
假設乙隊勝了a場、輸了b場,如下表
乙隊共出賽60場,所以a+b+1=60----(1)
所有比賽的勝場數等於負場數,即36+a+25+31=23+b+33+27 --- (2)
解上述二式
$$\begin{cases} a+b+1=60 \\ 36+a+25+31=23+b+33+27 \end{cases}\\ \Rightarrow \begin{cases} a+b=59 \\ a-b=-9 \end{cases}\Rightarrow a=25,b=34$$
故選(C)。
------------------------------------------------
20. 如圖(八),等臂天平的甲、乙兩秤盤都有5克、3克兩種砝碼,且乙秤盤比甲秤盤多2個砝碼。根據圖(八)的狀態,若甲的5克砝碼個數比乙多x個,則x的最小值為何?
(A) 2 (B) 3 (C) 4 (D) 5
解:
假設甲秤盤有5克砝碼a個、3克砝碼b個、乙秤盤有5克砝碼c個。
由「乙秤盤比甲秤盤多2個砝碼」可知:乙秤盤有3克砝碼a+b+2-c個。
由圖(八)可知甲秤盤比乙秤盤重,即
5a+3b>5c+3(a+b+2-c)⇒a-c>3,即x>3,故選(C)。
------------------------------------------------
21. 圖(九)是一個橫置的直角柱密閉容器ABCDEF,其底面積為直角三角形,內部裝有水,且矩形BCFE平放在水平地面上。今將此容器旋轉,使得矩形CADF平放在水平地面上,如圖(十)所示。已知AB=3,BC=4,AC=5,AD=10,且圖(九)中水的高度為2。若不計容器厚度,則圖(十)中水的高度為何?
(A) 4/5 (B) 6/5 (C) 8/5 (D) 2
解:
假設圖(九)的水平線為GH,其側面如下圖
AG/AB=GH/BC⇒1/3=GH/4⇒GH=4/3
梯形GHCB面積=(GH+BC)×GB/2=(4/3+4)×2/2=16/3;
假設圖(十)的水平線為MN,其側面如下圖
AB×BC=AC×BQ⇒3×4=BQ×5⇒BQ=12/5
AG/AB=GH/BC⇒1/3=GH/4⇒GH=4/3
梯形GHCB面積=(GH+BC)×GB/2=(4/3+4)×2/2=16/3;
假設圖(十)的水平線為MN,其側面如下圖
AB×BC=AC×BQ⇒3×4=BQ×5⇒BQ=12/5
$$\frac { \overline { BP } }{ \overline { BQ } } =\frac { \overline { MN } }{ \overline { CA } } \Rightarrow \frac { \frac { 12 }{ 5 } -h }{ \frac { 12 }{ 5 } } =\frac { \overline { MN } }{ 5 } \\ \Rightarrow 12-5h=\frac { 12 }{ 5 } \times \overline { MN } \Rightarrow \overline { MN } =5-\frac { 25 }{ 12 } h$$
梯形MNAC面積 =
$$\frac { \left( \overline { MN } +\overline { CA } \right) h }{ 2 } =\frac { \left( 5-\frac { 25 }{ 12 } h+5 \right) h }{ 2 } =5h-\frac { 25 }{ 24 } { h }^{ 2 }$$
水體積相同,所以梯形GHCB面積=梯形MNAC面積,即
$$5h-\frac { 25 }{ 24 } { h }^{ 2 }=\frac { 16 }{ 3 } \Rightarrow 15h-\frac { 25 }{ 8 } { h }^{ 2 }=16\\ \Rightarrow 25{ h }^{ 2 }-120h+128=0\Rightarrow (5h-16)(5h-8)\\ \Rightarrow h=\frac { 16 }{ 5 } or\frac { 8 }{ 5 } $$
由於h<BQ,h=16/5不合,故h=8/5,故選(C)。
------------------------------------------------
22. 若干對夫妻參加新婚座談會,座談會有提供參加的夫妻每人一杯飲料,其中飲料有茶、咖啡、果汁三種選擇。若座談會中丈夫選擇茶、咖啡、果汁的杯數比為5:3:2,妻子選擇茶、咖啡、果汁的杯數比為2:2:1,則所有參加者選擇茶、咖啡、果汁的杯數比為何?
(A) 7:5:3 (B) 9:7:4 (C) 16:12:7 (D) 20:16:9
解:
丈夫選擇茶、咖啡、果汁的杯數分別為5M、3M、2M;
妻子選擇茶、咖啡、果汁的杯數分別為2N、2N、N。
丈夫人數等於妻子人數,即5M+3M+2M=2N+2N+N⇒10M=5N⇒N=2M
所有參加者選擇茶、咖啡、果汁的杯數比為
(5M+2N):(3M+2N):(2M+N) = (5M+4M):(3M+4M):(2M+2M)
=9M:7M:4M=9:7:4,故選(B)。
------------------------------------------------
------------------------------------------------

解:
由於∠EOB=∠OFC=90°, 且∠B=∠C(△ABC為等腰), 因此兩三角形符合AAA,又OE=OF=3(半徑),所以△EOB與△OFC全等(ASA)。
令BO=a=FC, 則OC2=OF2+FC2, 即
$${ \overline { OC } }^{ 2 }={ \overline { OF } }^{ 2 }+{ \overline { FC } }^{ 2 }={ 3 }^{ 2 }+{ a }^{ 2 }\\ \Rightarrow \overline { OC } =\sqrt { { 3 }^{ 2 }+{ a }^{ 2 } } $$
又BC=BO+OC=6, 即
$$\quad a+\sqrt { { 3 }^{ 2 }+{ a }^{ 2 } } =6\Rightarrow { 3 }^{ 2 }+{ a }^{ 2 }={ \left( a-6 \right) }^{ 2 }={ a }^{ 2 }-12a+36\\ \Rightarrow 12a=27\Rightarrow a=\frac { 9 }{ 4 } $$
故選(D)。
------------------------------------------------
由於半徑與切點垂直,甲的作法找C、D兩切點的垂線交點,所以正確。
由於BD=BE,∠DBE的角平分線會經過圓心,E點為切點,其垂線也經過圓心,所以作法正確。
故選(A)。
--- END ---
------------------------------------------------
------------------------------------------------
------------------------------------------------
------------------------------------------------

























wow
回覆刪除.....
刪除???
刪除謝謝解答
回覆刪除沒有非選嗎
回覆刪除沒有
刪除有吧
刪除計算題?
回覆刪除沒
刪除不對‘有
刪除