106年公務、關務人員升官等考試
106年交通事業鐵路、公路、港務人員升資考試
等 級:薦任
類科(別):物理
科 目:微積分
微積分 詳解
解:$$y={ x }^{ x }={ e }^{ \ln { { x }^{ x } } }={ e }^{ x\ln { { x } } }\Rightarrow \frac { dy }{ dx } ={ e }^{ x\ln { { x } } }\cdot \left( \ln { { x } } +1 \right) =\bbox[red,2pt]{\left( \ln { { x } } +1 \right) { x }^{ x } }$$
解:$$x^{ 3 }+y^{ 3 }-9xy=0\Rightarrow 3x^{ 2 }+3y^{ 2 }\frac { dy }{ dx } -9y-9x\frac { dy }{ dx } =0\Rightarrow \left( 3y^{ 2 }-9x \right) \frac { dy }{ dx } =9y-3x^{ 2 }\\ \Rightarrow \frac { dy }{ dx } =\frac { 9y-3x^{ 2 } }{ 3y^{ 2 }-9x } =\frac { 3y-x^{ 2 } }{ y^{ 2 }-3x } \Rightarrow \left. \frac { dy }{ dx } \right| _{ (4,2) }=\frac { 6-16 }{ 4-12 } =\frac { 10 }{ 8 } =\frac { 5 }{ 4 } \\ \Rightarrow 過\left( 4,2 \right) ,斜率為\frac { 5 }{ 4 } 的切線方程式為y-2=\frac { 5 }{ 4 } \left( x-4 \right) \Rightarrow y=\frac { 5 }{ 4 } x-3\\ \Rightarrow a=\bbox[red,2pt]{\frac { 5 }{ 4 }} ,b=\bbox[red,2pt]{-3} $$
解:$$\frac { 1 }{ 2 } \int _{ 0 }^{ 2\pi }{ r^{ 2 } } d\theta =\frac { 1 }{ 2 } \int _{ 0 }^{ 2\pi }{ 4\left( 1+\cos { \theta } \right) ^{ 2 } } d\theta =2\int _{ 0 }^{ 2\pi }{ 1+2\cos { \theta } +\cos ^{ 2 }{ \theta } } d\theta \\ =2\left. \left[ \theta +2\sin { \theta } +\frac { 1 }{ 2 } \theta +\frac { 1 }{ 4 } \sin { 2\theta } \right] \right| ^{ 2\pi }_{ 0 }=2\left. \left[ \frac { 3 }{ 2 } \theta +2\sin { \theta } +\frac { 1 }{ 4 } \sin { 2\theta } \right] \right| ^{ 2\pi }_{ 0 }=\bbox[red,2pt]{6\pi} $$
解:$$\begin{cases} x=r\cos { \theta } \\ y=r\sin { \theta } \end{cases}\Rightarrow 1\le x^{ 2 }+y^{ 2 }\le 4\Rightarrow 1\le r^{ 2 }\le 4\Rightarrow 1\le |r|\le 2\\ \left| x^{ 2 }+y^{ 2 }+3y \right| =\left| r^{ 2 }+3r\sin { \theta } \right| \le r^{ 2 }+3\left| r \right| =4+3\times 2=10(r=2)\\ \left| r^{ 2 }-3r \right| \le \left| r^{ 2 }+3r\sin { \theta } \right| \Rightarrow r=1\Rightarrow \left| r^{ 2 }-3r \right| =2$$絕對最大值為\(\bbox[red,2pt]{10}\);絕對最小值為\(\bbox[red,2pt]{2}\)
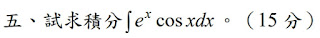
解:$$\begin{cases} u={ e }^{ x } \\ dv=\sin { x } dx \end{cases}\Rightarrow \begin{cases} du={ e }^{ x }dx \\ v=-\cos { x } \end{cases}\Rightarrow \int { { e }^{ x }\sin { x } } dx=-{ e }^{ x }\cos { x } +\int { { e }^{ x }\cos { x } } dx\\ \begin{cases} u={ e }^{ x } \\ dv=\cos { x } dx \end{cases}\Rightarrow \begin{cases} du={ e }^{ x }dx \\ v=\sin { x } \end{cases}\Rightarrow \int { { e }^{ x }\cos { x } } dx={ e }^{ x }\sin { x } -\int { { e }^{ x }\sin { x } } dx\\ ={ e }^{ x }\sin { x } -\left( -{ e }^{ x }\cos { x } +\int { { e }^{ x }\cos { x } } dx \right) ={ e }^{ x }\sin { x } +{ e }^{ x }\cos { x } -\int { { e }^{ x }\cos { x } } dx\\ \Rightarrow 2\int { { e }^{ x }\cos { x } } dx={ e }^{ x }\sin { x } +{ e }^{ x }\cos { x } \Rightarrow \int { { e }^{ x }\cos { x } } dx=\bbox[red,2pt]{\frac { 1 }{ 2 } { e }^{ x }\left( \sin { x } +\cos { x } \right) +C }$$
解:$$\lim _{ x\to 0 }{ \left( \frac { 1 }{ \sin { x } } -\frac { 1 }{ x } \right) } =\lim _{ x\to 0 }{ \frac { x-\sin { x } }{ x\sin { x } } } =\lim _{ x\to 0 }{ \frac { 1-\cos { x } }{ \sin { x } +x\cos { x } } } \\ =\lim _{ x\to 0 }{ \frac { \sin { x } }{ \cos { x } +\cos { x } -x\sin { x } } } =\frac { 0 }{ 2 } =\bbox[red,2pt]{0}$$
解:$$f\left( x \right) =f\left( a \right) +f'\left( a \right) \left( x-a \right) +\frac { f''\left( a \right) }{ 2! } { \left( x-a \right) }^{ 2 }+\frac { f'''\left( a \right) }{ 3! } { \left( x-a \right) }^{ 3 }+\cdots \\ x=\frac { \pi }{ 4 } \Rightarrow \sin { x } =\sin { \frac { \pi }{ 4 } } +\cos { \frac { \pi }{ 4 } } \left( x-\frac { \pi }{ 4 } \right) +\frac { -\sin { \frac { \pi }{ 4 } } }{ 2 } \left( x-\frac { \pi }{ 4 } \right) ^{ 2 }+\frac { -\cos { \frac { \pi }{ 4 } } }{ 6 } \left( x-\frac { \pi }{ 4 } \right) ^{ 3 }+\cdots \\ =\bbox[red,2pt]{\frac { \sqrt { 2 } }{ 2 } +\frac { \sqrt { 2 } }{ 2 } \left( x-\frac { \pi }{ 4 } \right) -\frac { \sqrt { 2 } }{ 4 } \left( x-\frac { \pi }{ 4 } \right) ^{ 2 }-\frac { \sqrt { 2 } }{ 12 } \left( x-\frac { \pi }{ 4 } \right) ^{ 3 }+\cdots }$$
考選部未公布答案,解題僅供參考

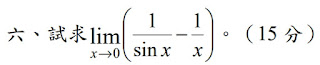
沒有留言:
張貼留言