98年大學學測數學詳解

98 學年度學科能力測驗

數學科詳解

一、單選題

1. 數列$a_1 + 2,\cdots,a_k+2k,\cdots,a_{10} + 20$共有十項，且其和為 240，則 $a_1+\cdots+a_k+\cdots+a_{10}$之值為

(1) 31 (2) 120 (3) 130 (4) 185 (5) 218

解： $$(a_1 + 2)+\cdots+(a_k+2k)+\cdots+(a_{10} + 20)=\sum_{k=1}^{10}{(a_k+2k)}=\sum_{k=1}^{10}{a_k}+2\sum_{k=1}^{10}{k}\\ =\sum_{k=1}^{10}{a_k}+2\times 55=\sum_{k=1}^{10}{a_k}+110=240\Rightarrow \sum_{k=1}^{10}{a_k}=240-110=130,\\故選\bbox[red,2pt]{(3)}$$

---

2. 令 $a = \cos{(π^2 )}$，試問下列哪一個選項是對的？

(1)$a=-1$  (2)$-1<a\le-\frac{1}{2}$  (3)$-\frac{1}{2}<a\le 0$ (4) $0<a\le \frac{1}{2}$  (5) $\frac{1}{2}<a\le 1$

解：

$$a=\cos{(\pi^2)}=\cos{(3.14\pi)}=\cos{(1.14\pi)}=\cos{(1.14\times 180^\circ)}= \cos{205^\circ}\\ \Rightarrow \cos{180^\circ}< a <\cos{240^\circ} \Rightarrow -1<a<-\frac{1}{2}$$ ，故選$\bbox[red,2pt]{(2)}$

---

3. 已知 f (x), g(x)是兩個實係數多項式，且知 f (x)除以g(x)的餘式為$x^4 −1$。試問下列哪一個選項不可能是 f (x)與g(x)的公因式？

(1) 5 (2) x-1 (3) $x^2-1$ (4) $x^3-1$  (5)$x^4-1$

解：

被除式與除式的公因式=除式與餘式的公因式；
也就是說f (x)與g(x)的公因式=g(x)與$x^4 −1$的公因式；
$x^4-1=(x^2-1)(x^2+1)=(x+1)(x-1)(x^2+1)\Rightarrow (x+1),(x-1),(x^2-1),(x^2+1)$都可能是公因式；又常數是任何多項式的因式，故選$\bbox[red,2pt]{(4)}$

---

4. 甲、乙、丙三所高中的一年級分別有3、4、5 個班級。從這12 個班級中隨機選取一班參加國文抽考，再從未被抽中的11 個班級中隨機選取一班參加英文抽考。則參加抽考的兩個班級在同一所學校的機率最接近以下哪個選項？

(1) 21% (2) 23% (3) 25% (4) 27% (5) 29%

解：

兩次抽考都抽中甲校的機率為$\frac{3}{12}\times\frac{2}{11}$；
兩次抽考都抽中乙校的機率為$\frac{4}{12}\times\frac{3}{11}$；
兩次抽考都抽中丙校的機率為$\frac{5}{12}\times\frac{4}{11}$；
因此兩次都抽中同校的機率為$\frac{3}{12}\times\frac{2}{11} +\frac{4}{12}\times\frac{3}{11} +\frac{5}{12}\times\frac{4}{11}=\frac{19}{66}\approx 0.29$，故選$\bbox[red,2pt]{(5)}$

---

5. 假設甲、乙、丙三鎮兩兩之間的距離皆為20 公里。兩條筆直的公路交於丁鎮，其中之一通過甲、乙兩鎮而另一通過丙鎮。今在一比例精準的地圖上量得兩公路的夾角為45°，則丙、丁兩鎮間的距離約為

(1) 24.5 公里 (2) 25 公里 (3) 25.5 公里 (4) 26 公里 (5) 26.5 公里

解：

由題意知: 甲、乙、丙構成一個正三角形，相對位置如上圖。
在$\triangle$丁乙丙中，$\frac{\overline{丙丁}}{\sin{\angle 乙}}=\frac{\overline{乙丙}}{\sin{\angle 丁}}\Rightarrow \frac{\overline{丙丁}}{\sin{60^\circ}}=\frac{20}{\sin{45^\circ}} \Rightarrow  \frac{\overline{丙丁}}{\sqrt{3}/2}=\frac{20}{\sqrt{2}/2}\Rightarrow \overline{丙丁}=\frac{20\sqrt{3}}{\sqrt{2}}=24.5$

故選$\bbox[red,2pt]{(1)}$

---

6. 試問坐標平面上共有幾條直線，會使得點O(0,0)到此直線之距離為 1，且點 A(3,0)到此直線之距離為2？

(1) 1 條 (2) 2 條 (3) 3 條 (4) 4 條 (5)無窮多條

解：

三條藍色的公切線(見上圖)符合要求，故選$\bbox[red,2pt]{(3)}$

---

二、多選題

解： $$(1)\bigcirc: 有限小數是有理數\\(2)\times: \sqrt{3}不是有理數\\(3)\bigcirc: \log_{10}{\sqrt{5}}+\log_{10}{\sqrt{2}}=\log_{10}{\sqrt{10}}=\frac{1}{2}是有理數\\(4)\bigcirc: \frac{\sin{15^\circ}}{\cos{15^\circ}}+\frac{\cos{15^\circ}}{\sin{15^\circ}} =\frac{\sin^2{15^\circ}+\cos^2{15^\circ}}{\sin{15^\circ}\cos{15^\circ}}=\frac{1}{\frac{1}{2}\sin{30^\circ}}=4是有理數\\ (5)\times: 令f(x)=x^3-2x^2+x-1, 依有理根判別法, f(\pm 1) \ne 0,即 f(x)=0實根不為有理數$$

故選$\bbox[red,2pt]{(1,3,4)}$

---

8. 坐標平面上四條直線$L_1,L_2 ,L_3 ,L_4$與x軸、 y軸及直線 y = x的相關位置如圖所示，其中$L_1$ 與$L_3$ 垂直，而$L_3$ 與$L_4$ 平行。設$L_1,L_2 ,L_3 ,L_4$的方程式分別為$y=m_1x , y=m_2x , y = m_3x$以及$y = m_4 x + c$ 。試問下列哪些選項是正確的？

(1) $m_3>m_2>m_1$  (2) $m_1\cdot m_4=-1$  (3) $m_1<-1$  (4) $m_2\cdot m_3<-1$  (5) c>0

解：

$$(1)\times :應該是 m_3>m_1>m_2\\ (2)\bigcirc :\begin{cases}L_1\bot L_3\\ L_3//L_4 \end{cases}\Rightarrow L_4\bot L_1\Rightarrow m_1\cdot m_4=-1\\ (3)\bigcirc :\begin{cases}1>m_4>0\\m_1\cdot m_4=-1\end{cases}\Rightarrow m_1<-1 \\ (4)\bigcirc :\begin{cases}m_1\cdot m_3=m_1\cdot m_4=-1\\m_2<m_1<-1\end{cases}\Rightarrow m_2\cdot m_3<-1\\(5)\times :L_4的Y軸截距為負\Rightarrow c<0$$

答：$\bbox[red,2pt]{(2,3,4)}$

---

9. 某廠商委託民調機構在甲、乙兩地調查聽過某項產品的居民佔當地居民之百分比(以下簡稱為「知名度」)。結果如下：在95% 信心水準之下，該產品在甲、乙兩地的知名度之信賴區間分別為 [ 0.50 , 0.58 ]、[ 0.08 , 0.16 ]。試問下列哪些選項是正確的？
(1) 甲地本次的參訪者中， 54% 的人聽過該產品
(2) 此次民調在乙地的參訪人數少於在甲地的參訪人數
(3) 此次調查結果可解讀為：甲地全體居民中有一半以上的人聽過該產品的機率大於95%
(4) 若在乙地以同樣方式進行多次民調，所得知名度有95% 的機會落在區間[ 0.08 , 0.16 ]
(5) 經密集廣告宣傳後，在乙地再次進行民調，並增加參訪人數達原人數的四倍，則在95%信心水準之下該產品的知名度之信賴區間寬度會減半(即0.04)

解：

在95% 信心水準之下的信賴區間為$[p-2\sqrt{\frac{p(1-p)}{n}},p+2\sqrt{\frac{p(1-p)}{n}}]$
$$(1)\bigcirc: 甲的信賴區間為[0.50,0.58]=[0.54-0.04,0.54+0.0.4]\Rightarrow p=0.54\\(2)\bigcirc:\begin{cases}甲:[0.54-0.04,0.54+0.04]=[0.54-2\times 0.02,0.54+2\times 0.02]\\乙:[0.12-0.04,0.12+0.04] =[0.12-2\times 0.02,0.12+2\times 0.02]\end{cases}\Rightarrow \begin{cases}\sqrt{\frac{0.54(1-0.54)}{n_甲}}=0.02\\\sqrt{\frac{0.12(1-0.12)}{n_乙}}=0.02\end{cases}\\\Rightarrow \frac{0.54(1-0.54)}{n_甲}=\frac{0.12(1-0.12)}{n_乙}\Rightarrow \frac{0.54\times 0.46}{n_甲}=\frac{0.12\times 0.88}{n_乙}\Rightarrow \frac{大數}{n_甲}=\frac{小數}{n_乙}\Rightarrow n_甲>n_乙\\(3)\times:信賴區間並非如此解讀\\(4)\times: 信賴區間並非如此解讀\\(5)\times:增加參訪人數達原人數的四倍會減半信賴區間,但分子的p值已不同，\\因此無法保證信賴區間寬度減半$$

故選：$\bbox[red,2pt]{(1,2)}$

---

10. 設a,b,c為實數，下列有關線性方程組$\begin{cases}x+2y+az=1\\ 3x+4y+bz=-1\\ 2x+10y+7z=c\end{cases}$的敘述哪些是正確的？
(1) 若此線性方程組有解，則必定恰有一組解
(2) 若此線性方程組有解，則11a − 3b ≠ 7
(3) 若此線性方程組有解，則c =14
(4) 若此線性方程組無解，則11a − 3b = 7
(5) 若此線性方程組無解，則 c ≠14

解：

$$\begin{cases}x+2y+az=1\cdots(1)\\ 3x+4y+bz=-1\cdots(2)\\ 2x+10y+7z=c\cdots(3)\end{cases} \xrightarrow{式1\times(-3)+式2,式1\times(-2)+式3} \begin{cases}2y+(3a-b)z=4\cdots(3)\\ 6y+(7-2a)z=c-2\cdots(4)\end{cases}\\ \Rightarrow \begin{cases}無解:\frac{2}{6}=\frac{3a-b}{7-2a}\ne\frac{4}{c-2}\\\begin{cases}只有一解:\frac{2}{6}\ne\frac{3a-b}{7-2a}\\無限多解:\frac{2}{6}=\frac{3a-b}{7-2a}=\frac{4}{c-2}\end{cases}\end{cases}\Rightarrow \begin{cases}無解:11a-3b=7且c\ne 14\\\begin{cases}只有一解:11a-3b\ne7\\無限多解:11a-3b=7且c=14\end{cases}\end{cases}$$  

故選：$\bbox[red,2pt]{(4,5)}$

---

11. 如圖所示，正立方體 ABCD - EFGH 的稜長等於 2 (即$\overline{AB} = 2$ )，K 為正方形ABCD的中心，M 、N 分別為線段BF 、EF 的中點。試問下列哪些選項是正確的？

(1)$\overrightarrow{KM}=\frac{1}{2}\overrightarrow{AB}-\frac{1}{2}\overrightarrow{AD} +\frac{1}{2}\overrightarrow{AE}$

(2) (內積)$\overrightarrow{KM}\cdot\overrightarrow{AB}=1$

(3) $\overline{KM}=3$

(4)ΔKMN 為一直角三角形

(5) ΔKMN 之面積為$\frac{\sqrt{10}}{2}$

解：

假設E為原點，X軸、Y軸及Z軸如上圖所示，則$A=(0,0,2), B=(0,2,2), C=(2,2,2), D=(2,0,2), E=(0,0,0)$,
$F=(0,2,0), G=(2,2,0), M=(0,2,1), N=(0,1,0), K=(1,1,2)$
(1)$\bigcirc:\overrightarrow{KM}=(0-1,2-1,1-2)=(-1,1,-1);$ ，而$\frac{1}{2} \overrightarrow{AB}-\frac{1}{2}\overrightarrow{AD} +\frac{1}{2}\overrightarrow{AE}$
$=\frac{1}{2}(0,2,0)-\frac{1}{2}(2,0,0) +\frac{1}{2}(0,0,-2)= (0,1,0)-(1,0,0)+(0,0,-1)=(-1,1,-1)$，兩者相等；
(2)$\times:\overrightarrow{KM}\cdot\overrightarrow{AB}=(-1,1,-1)\cdot (0,2,0)=0+2+0=2\ne 0$
(3)$\times:\overline{KM}=\sqrt{1^2+(-1)^2+1^2}=\sqrt{3}\ne 3$
(4)$\bigcirc:\overrightarrow{KM}\cdot\overrightarrow{MN}=(-1,1,-1)\cdot(0,-1,-1) =0 \Rightarrow \angle KMN=90^\circ$
(5)$\times: \triangle KMN面積=\overline{KM}\times\overline{MN}\div 2=\sqrt{3}\times \sqrt{2} \div 2=\frac{\sqrt{6}}{2}\ne \frac{\sqrt{10}}{2}$

故選$\bbox[red,2pt]{(1,4)}$

---

第二部分：選填題

A. 從1 到100 的正整數中刪去所有的質數、2 的倍數及3 的倍數之後，剩下最大的數為？

解：  

100: 2的倍數、99:3的倍數、98:2的倍數、97:質數、96:2的倍數、95、94:2的倍數....

答：$\bbox[red,2pt]{95}$

---

B. 坐標平面上有四點O(0,0) , A(−3,−5) , B(6,0) ,C(x, y)。今有一質點在O點沿$\overrightarrow{AO}$方向前進$\overline{AO}$ 距離後停在P，再沿$\overrightarrow{BP}$方向前進$2\overline{BP}$ 距離後停在Q。假設此質點繼續沿$\overrightarrow{CQ}$方向前進$3\overline{CQ}$ 距離後回到原點O，則(x, y)=？

解：

$$令P=(x_p,y_p),由\overrightarrow {AP}=2\overrightarrow{AO}\Rightarrow (x_p+3,y_p+5)=2(3,5)\Rightarrow P=(3,5)\\ 令Q=(x_q,y_q),由\overrightarrow {BQ}=3\overrightarrow{BP}\Rightarrow (x_q-6,y_q)=3(-3,5)\Rightarrow Q=(-3,15)\\ \overrightarrow {QO}=3\overrightarrow {CQ}\Rightarrow (3,-15)=3(-3-x,15-y)\Rightarrow C=\bbox[red,2pt]{(-4,20)}$$

---

C. 抽獎遊戲中，參加者自箱中抽出一球，確定顏色後放回。只有抽得藍色或紅色球者可得消費劵，其金額分別為(抽得藍色球者)2000 元、(抽得紅色球者)1000 元。箱中已置有2 顆藍色球及5 顆紅色球。在抽出任一球之機率相等的條件下，主辦單位希望參加者所得消費劵金額的期望值為300 元，則主辦單位應於箱內再置入？ 顆其他顏色的球

解：
假設放入其它色球$a$顆，則抽中藍球的機率為$\frac{2}{2+5+a}=\frac{2}{7+a}$，抽中紅球的機率為$\frac{5}{7+a}$，期望值為$\frac{2}{7+a}\times 2000+\frac{5}{7+a}\times 1000=\frac{9000}{7+a}=300 \Rightarrow a=23$；

答：放入$\bbox[red,2pt]{23}$顆其他色球

---

D. 坐標平面上有兩條平行直線。它們的x 截距相差20 ， y 截距相差15。則這兩條平行直線的距離為？

解： $$\begin{cases}L_1:y=mx+a\\L_2:y=mx+b\end{cases}\Rightarrow \begin{cases}L_1:x截距-a/m,y截距a\\L_2:x截距-b/m,y截距b\end{cases}\\\Rightarrow \begin{cases}\left|\frac{a-b}{m}\right|=20\\|a-b|=15\end{cases}\Rightarrow |m|=\frac{15}{20}=\frac{3}{4}\Rightarrow 兩平行線相距\left|\frac{a-b}{\sqrt{m^2+1}}\right|=\left|\frac{15}{5/4}\right|=\bbox[red,2pt]{12}$$

---

E. 假設$\Gamma_1$ 為坐標平面上一開口向上的拋物線，其對稱軸為$x=-\frac{3}{4}$且焦距（焦點到頂點的距離）為$\frac{1}{8}$。若$\Gamma_1$ 與另一拋物線$\Gamma_2: y = x^2$ 恰交於一點，則$\Gamma_1$ 的頂點之y 坐標為 ？。(化成最簡分數)

解： $$假設\Gamma_1的頂點坐標為(-\frac{3}{4},a)\Rightarrow \Gamma_1:(x+\frac{3}{4})^2=4\cdot\frac{1}{8}\cdot(y-a)=\frac{1}{2}(y-a)\\將\Gamma_2:y=x^2代入\Gamma_1\Rightarrow (x+\frac{3}{4})^2=\frac{1}{2}(x^2-a)\Rightarrow x^2+3x+\frac{9}{8}+a=0\\由於只有一組解，所以判別式=0\Rightarrow 9-4(\frac{9}{8}+a)=0\Rightarrow a=\bbox[red,2pt]{\frac{9}{8}}$$

---

F. 某公司為了響應節能減碳政策，決定在五年後將公司該年二氧化碳排放量降為目前排放量的75%。公司希望每年依固定的比率(當年和前一年排放量的比)逐年減少二氧化碳的排放量。若要達到這項目標，則該公司每年至少要比前一年減少 ？ % 的二氧化碳的排放量。(計算到小數點後第一位，以下四捨五入。)

解：

$$(1+r)^5=0.75=\frac{3}{4}\Rightarrow 5\log{(1+r)}= \log{3}-2\log{2}\Rightarrow \log{(1+r)} =\frac{0.4771-2\times 0.301}{5}\\ =-0.02498 =-1+0.97502 \xrightarrow{查表}-1+\log{9.445}= \log{0.9445}\\\Rightarrow 1+r=0.9445\Rightarrow r=-0.0555,即減少 \bbox[red,2pt]{5.6\%}$$

---

G. 坐標空間中xy平面上有一正方形，其頂點為O(0,0,0) , A(8,0,0) , B(8,8,0) ,C(0,8,0)。另一點P在xy平面的上方，且與 O, A, B, C 四點的距離皆等於 6。若x + by + cz = d 為通過 A, B , P三點的平面，則(b,c,d) =？

解：

令$P=(4,4,a), Q$為P在XY平面上的投影點，所以Q=(4,4,0)；

在直角$\triangle PQB$中，$\overline{PB}^2=\overline{QP}^2+\overline{QB}^2 \Rightarrow 6^2=a^2+((8-4)^2+(8-4)^2+0^2)\Rightarrow a=2$

$x+by+cz=d$經過A, B , P三點，即

$$\begin{cases}8+0+0=d\\8+8b=d\\4+4b+2c=d\end{cases}\Rightarrow \begin{cases}d=8\\b=0\\c=2\end{cases} \Rightarrow (b,c,d)=\bbox[red,2pt]{0,2,8}$$

---

H. 有一橢圓與一雙曲線有共同的焦點$F_1,F_2$，且雙曲線的貫軸長和橢圓的短軸長相等。設P 為此橢圓與雙曲線的一個交點，且$\overline{PF_1}\times\overline{PF_2} = 64$，則$\overline{F_1F_2} =$？

解：

$$令\begin{cases}橢圓: \frac{x^2}{a_1^2}+\frac{y^2}{b_1^2}=1\\雙曲線: \frac{x^2}{a_2^2}-\frac{y^2}{b_2^2}=1\end{cases} \Rightarrow \begin{cases}\overline{PF_1}+\overline{PF_2}=2a_1\\\overline{PF_1}-\overline{PF_2}=2a_2\end{cases} \\\Rightarrow \left(\overline{PF_1}+\overline{PF_2}\right)^2-\left(\overline{PF_1}-\overline{PF_2}\right)^2=4a_1^2-4a_2^2\\\Rightarrow 4\overline{PF_1}\times\overline{PF_2}=4a_1^2-4a_2^2\Rightarrow \overline{PF_1} \times \overline{PF_2} =a_1^2-a_2^2=64\\由雙曲線的貫軸長和橢圓的短軸長相等\equiv 2a_2=2b_1\Rightarrow a_2=b_1\Rightarrow a_1^2-b_1^2=c_1^2=64\\ \Rightarrow c_1=8\Rightarrow \overline{F_1F_2}=2c_1=2\times 8=\bbox[red,2pt]{16}$$

---

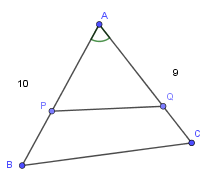
I. 在ΔABC 中，$\overline{AB} =10 , \overline{AC} = 9 , \cos{\angle BAC}=\frac{3}{8}$。設點 P、Q 分別在邊 AB、AC上使得ΔAPQ之面積為ΔABC面積之一半，則$\overline{PQ}$之最小可能值為 ？。(化成最簡分數)

解：

$$\frac{\triangle APQ}{\triangle ABC}=\frac{1}{2}\Rightarrow \frac{\overline{AP}\times\overline{AQ}} {\overline{AB}\times \overline{AC}}=\frac{1}{2}\Rightarrow \frac{\overline{AP}\times\overline{AQ}} {10\times 9}=\frac{1}{2} \Rightarrow \overline{AP}\times\overline{AQ}=45\\在\triangle APQ 中\Rightarrow \cos{\angle A}=\frac{\overline{AP}^2 +\overline{AQ}^2 -\overline{PQ}^2}{2\overline{AP}\times\overline{AQ}} \Rightarrow \frac{3}{8}=\frac{\overline{AP}^2 +\overline{AQ}^2 -\overline{PQ}^2}{2\times 45}\\\Rightarrow \overline{AP}^2 +\overline{AQ}^2 -\overline{PQ}^2=\frac{135}{4} \Rightarrow \overline{PQ}=\sqrt{\overline{AP}^2 +\overline{AQ}^2 -\frac{135}{4}}\\ 由於\frac{\overline{AP}^2 +\overline{AQ}^2}{2} \ge \sqrt{\overline{AP}^2 \times\overline{AQ}^2}=\overline{AP}\times\overline{AQ}=45 \Rightarrow \overline{AP}^2 +\overline{AQ}^2\ge 90\\ \Rightarrow \overline{PQ}=\sqrt{\overline{AP}^2 +\overline{AQ}^2 -\frac{135}{4}}\ge \sqrt{90-\frac{135}{4}}=\sqrt{\frac{225}{4}}=\bbox[red,2pt]{\frac{15}{2}}$$

========================== END ========================

解題僅供參考,其他歷年試題及詳解