解:
$$2^{2x}-5\cdot 2^x-24=0\Rightarrow (2^x-8)(2^x+3)=0\Rightarrow 2^x=8\Rightarrow x=3,故選\bbox[red,2pt]{(C)}。$$
解:\(P(a,b)\)在第二象限\(\Rightarrow \begin{cases}a<0\\b>0\end{cases} \Rightarrow \begin{cases}ab<0\\b-a>0\end{cases}\Rightarrow \)點\(Q(ab,b-a)\)也在第二象限,故選\(\bbox[red,2pt]{(B)}\)。
解:只看常數項,即\(-30=(-2)\times (-5)\times (-a)=-10a\Rightarrow a=3\),故選\(\bbox[red,2pt]{(C)}\)。
解:
令\(f(x)=x^{50}+x^{30}-a\),由題意知:\(f(1)=0\Rightarrow 1+1-a=0\Rightarrow a=2\),故選\(\bbox[red,2pt]{(A)}\)。
解:$$\begin{cases} 2^{ x }=100 \\ 20^{ y }=100 \end{cases}\Rightarrow \begin{cases} \log { 2^{ x } } =\log { 100 } \\ \log { 20^{ y } } =\log { 100 } \end{cases}\Rightarrow \begin{cases} x\log { 2 } =2 \\ y\left( 1+\log { 2 } \right) =2 \end{cases}\\ \Rightarrow \begin{cases} \frac { 1 }{ x } =\frac { \log { 2 } }{ 2 } \\ \frac { 1 }{ y } =\frac { 1+\log { 2 } }{ 2 } \end{cases}\Rightarrow \frac { 1 }{ x } -\frac { 1 }{ y } =\frac { \log { 2 } }{ 2 } -\frac { 1+\log { 2 } }{ 2 } =-\frac { 1 }{ 2 } ,故選\bbox[red,2pt]{(D)}。$$
解:$$\frac { \sin { 5° } +\sin { 10° } }{ 1+\cos { 5° } +\cos { 10° } } =\frac { \sin { 5° } +2\sin { 5° } \cos { 5° } }{ 1+\cos { 5° } +2\cos ^{ 2 }{ 5° } -1 } =\frac { \sin { 5° } \left( 1+2\cos { 5° } \right) }{ \cos { 5° } \left( 1+2\cos { 5° } \right) } =\frac { \sin { 5° } }{ \cos { 5° } } \\ =\tan { 5° } ,故選\bbox[red,2pt]{(C)}。$$
解:
由\(a^2=b^2+c^2\)可知\(\angle A=90^\circ\),如上圖;因此\(sec{\theta}+\csc{\theta}=\frac{a}{c}+\frac{a}{b}=\frac{a(b+c)}{bc}\),故選\(\bbox[red,2pt]{(B)}\)。
解:$$f\left( \theta \right) =4\sin { \theta } +3\cos { \theta } =5\left( \frac { 4 }{ 5 } \sin { \theta } +\frac { 3 }{ 5 } \cos { \theta } \right) =5\left( \cos { \alpha } \sin { \theta } +\sin { \alpha } \cos { \theta } \right) \\ =5\sin { \left( \theta +\alpha \right) } \Rightarrow -5\le f\left( \theta \right) \le 5,故選\bbox[red,2pt]{(C)}。$$
解:$$\frac { x+y }{ 2 } \ge \frac { 2 }{ \frac { 1 }{ x } +\frac { 1 }{ y } } \Rightarrow \frac { 4 }{ 2 } \ge \frac { 2 }{ \frac { 1 }{ x } +\frac { 1 }{ y } } \Rightarrow \frac { 1 }{ x } +\frac { 1 }{ y } \ge 1,故選\bbox[red,2pt]{(A)}。$$
解:
該區域為一正方形,如上圖,其邊長為\(4\sqrt{2}\Rightarrow \)面積為\(4\sqrt{2}\times 4\sqrt{2}=32\),故選\(\bbox[red,2pt]{(D)}\)。
解:
由圖形可知: (0,6)至(0,-6)的距離最大,即12,故選\(\bbox[red,2pt]{(B)}\)。
解:
等號左邊要能將\(k\)消掉,\(y\)必須為1;\(y=1\)代入原式可得\(x^2+1-2x+(k+6)-k=6 \Rightarrow x^2-2x+1=0\Rightarrow x=1\);因此當\(x=y=1\)時,原式恆成立,故選\(\bbox[red,2pt]{(D)}\)。
解:$$a:b:c=5:7:8\Rightarrow \begin{cases} a=5k \\ b=7k \\ c=8k \end{cases},k為常數\Rightarrow \cos { \angle B } =\frac { a^{ 2 }+c^{ 2 }-b^{ 2 } }{ 2ac } =\frac { 25k^{ 2 }+64k^{ 2 }-49k^{ 2 } }{ 2\times 5k\times 8k } \\ =\frac { 40k^{ 2 } }{ 80k^{ 2 } } =\frac { 1 }{ 2 } \Rightarrow \angle B=\frac { \pi }{ 3 } =60°,故選\bbox[red,2pt]{(A)}。$$
解:$$\vec{u}\cdot\vec{v}=|\vec{u}||\vec{v}|\cos{30^\circ}=1\times 1\times\frac{\sqrt{3}}{2}=\frac{\sqrt{3}}{2},故選\bbox[red,2pt]{(C)}。$$
解:$$令\begin{cases} \vec { a } =(1,0) \\ \vec { b } =(2,0) \\ \vec { c } =(-3,0) \end{cases},則\vec { a } \cdot \vec { b } +\vec { b } \cdot \vec { c } +\vec { c } \cdot \vec { a } =\left| \vec { a } \right| \left| \vec { b } \right| \cos { 0° } +\left| \vec { b } \right| \left| \vec { c } \right| \cos { 180° } +\left| \vec { c } \right| \left| \vec { a } \right| \cos { 180° } \\ =2-6-3=-7,故選\bbox[red,2pt]{(D)}。$$
解:$$\left| z_{ 1 }z_{ 2 }=|z_{ 1 }||z_{ 2 } \right| \Rightarrow \left| \left( 3+4i \right) \left( 12-5i \right) \right| =\left| 3+4i \right| \left| 12-5i \right| \\=\sqrt { 3^{ 2 }+4^{ 2 } } \times \sqrt { 12^{ 2 }+5^{ 2 } } =5\times 13=65 ,故選\bbox[red,2pt]{(C)}。$$
解:$${ \left( \sqrt { 3 } -i \right) }^{ 3 }={ \left( \sqrt { 3 } -i \right) }^{ 2 }\left( \sqrt { 3 } -i \right) =\left( 3-2\sqrt { 3 } i-1 \right) \left( \sqrt { 3 } -i \right) =\left( 2-2\sqrt { 3 } i \right) \left( \sqrt { 3 } -i \right) \\ =2\sqrt { 3 } -2i-6i-2\sqrt { 3 } =-8i,故選\bbox[red,2pt]{(A)}。$$
解:$$\left| \begin{matrix} 1 & 0 & x \\ -2 & 3 & 4 \\ 1 & x & -1 \end{matrix} \right| =\left| \begin{matrix} 2x & 1 \\ 1 & -x \end{matrix} \right| \Rightarrow -3-2x^2-3x-4x=-2x^2-1\Rightarrow 7x=-2\\\Rightarrow x=-\frac{2}{7},故選\bbox[red,2pt]{(B)}。$$
解:$$2x^{ 2 }+y^{ 2 }+4x+2y+1=0\Rightarrow 2(x^{ 2 }+2x+1)+(y^{ 2 }+2y+1)=2\Rightarrow 2(x+1)^{ 2 }+(y+1)^{ 2 }=2\\ \Rightarrow \frac { (x+1)^{ 2 } }{ 1 } +\frac { (y+1)^{ 2 } }{ 2 } =1,故選\bbox[red,2pt]{(D)}。$$
解:$$9x^{ 2 }-y^{ 2 }+36x+2y+26=0\Rightarrow 9(x^{ 2 }+4x+4)-(y^{ 2 }-2y+1)=9\Rightarrow 9(x+2)^{ 2 }-(y-1)^{ 2 }=9\\ \Rightarrow \frac { (x+2)^{ 2 } }{ 1 } -\frac { (y-1)^{ 2 } }{ 9 } =1\Rightarrow 中心坐標(-2,1),故選\bbox[red,2pt]{(A)}。$$
解:$$f\left( x \right) =x^{ 2 }+4x+2\Rightarrow f'(x)=2x+4\Rightarrow \lim _{ x\to 2 }{ \frac { f\left( x \right) -f\left( 2 \right) }{ x-2 } } =f'(2)=2\times 2+4=8 ,故選\bbox[red,2pt]{(B)}。$$
解:$$f\left( x \right) =x^{ 3 }-3x^{ 2 }-9x\Rightarrow f'(x)=3x^{ 2 }-6x-9\Rightarrow f''(x)=6x-6\\ f'(x)=0\Rightarrow 3x^{ 2 }-6x-9=0\Rightarrow 3(x^{ 2 }-2x-3)=0\Rightarrow 3(x-3)(x+1)=0\Rightarrow x=3,-1\\ \Rightarrow \begin{cases} f''(3)=18-6=12>0 \\ f''(-1)=-6-6=-12<0 \end{cases}\Rightarrow f\left( 3 \right) =27-27-27=-27為相對極小值,故選\bbox[red,2pt]{(D)}。$$
解:$$\lim _{ x\to 1 }{ \frac { ax^{ 2 }+bx+2 }{ x-1 } } =1\Rightarrow ax^{ 2 }+bx+2=\left( mx+n \right) (x-1)\Rightarrow \begin{cases} m+n=1 \\ -n=2 \end{cases}\Rightarrow \begin{cases} m=3 \\ n=-2 \end{cases}\\ \Rightarrow ax^{ 2 }+bx+2=\left( 3x-2 \right) (x-1)=3x^{ 2 }-5x+2\Rightarrow \begin{cases} a=3 \\ b=-5 \end{cases}\Rightarrow a+b=-2,故選\bbox[red,2pt]{(B)}。$$
解:
\(y=3-\left| x \right| \Rightarrow \begin{cases} y=3-x&x\ge0 \\ y=3+x&x\le 0\end{cases}\),圖形如上;因此所圍面積為\(6\times 3\div 2=9\),故選\(\bbox[red,2pt]{(C)}\)。
解:$$f\left( x \right) =3x^{ 2 }+ax+b\Rightarrow \begin{cases} f'(x)=6x+a \\ \int { f\left( x \right) dx } =x^{ 3 }+\frac { a }{ 2 } x^{ 2 }+bx+c \end{cases}\\ 因此\begin{cases} f'(1)=10 \\ \int _{ 0 }^{ 1 }{ f\left( x \right) dx } =5 \end{cases}\Rightarrow \begin{cases} 6+a=10 \\ 1+\frac { a }{ 2 } +b=5 \end{cases}\Rightarrow \begin{cases} a=4 \\ b=2 \end{cases}\Rightarrow a+b=6,故選\bbox[red,2pt]{(A)}。$$
--end--






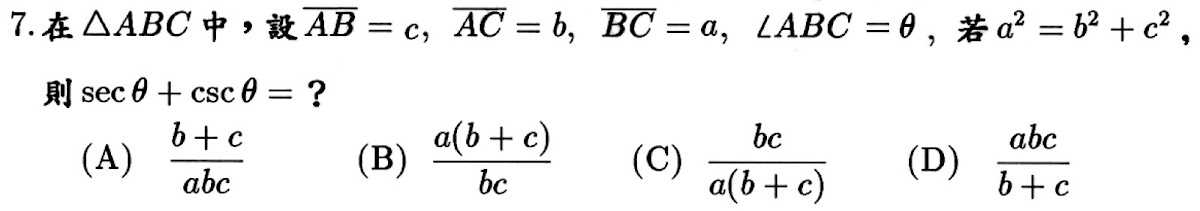






















沒有留言:
張貼留言