108學年度科技校院四年制與專科學校二年制
統一入學測驗試題本數學(C)詳解
$$\begin{cases} \vec { u } \bot \vec { v } \\ \vec { u } //\vec { w } \end{cases}\Rightarrow \begin{cases} \vec { u } \cdot \vec { v } =0 \\ \vec { u } =k\vec { w } \end{cases}\Rightarrow \begin{cases} \left( 1,1 \right) \cdot \left( x+4,y-1 \right) =0 \\ \left( 1,1 \right) =k\left( 2x,y \right) \end{cases}\Rightarrow \begin{cases} x+y+3=0 \\ 2x=y \end{cases}\\ \Rightarrow x+2x+3=0\Rightarrow x=-1\Rightarrow y=-2, 故選\bbox[red,2pt]{(B)}$$
A、D位於\(L_1\)的左側,即\(3x-5y\le 2\);A、B位於\(L_2\)的右側,即\(x+2y\ge 3\);
兩者交集即為區域A,故選\(\bbox[red,2pt]{(B)}\)。
$$假設半徑為r,角度為\theta ,則\begin{cases} r^{ 2 }\pi \times \frac { \theta }{ 2\pi } =1 \\ r\theta +2r=5 \end{cases}\Rightarrow \begin{cases} \theta =2/r^{ 2 } \\ r\theta +2r=5 \end{cases}\\ \Rightarrow r\cdot \frac { 2 }{ r^{ 2 } } +2r=5\Rightarrow \frac { 2r^{ 2 }-5r+2 }{ r } =0\Rightarrow \frac { \left( 2r-1 \right) \left( r-2 \right) }{ r } =0\\ \Rightarrow \begin{cases} r=1/2 \\ r=2 \end{cases}\Rightarrow \begin{cases} \theta =2/r^{ 2 }=8(不合,超過2\pi ) \\ \theta =2/r^{ 2 }=1/2 \end{cases},故選\bbox[red,2pt]{(D)}。$$
假設梯長\(\overline{AC}=\overline{DE}=a\),見上圖;
在\(\triangle ABC\)中,\(\overline{BC}=\frac{a}{\sqrt{2}}\);在\(\triangle DBE\)中,\(\overline{BC}=\overline{BD}-\overline{DC}=\frac{\sqrt{3}a}{2}-1/2\);
因此\(\frac{a}{\sqrt{2}}=\frac{\sqrt{3}a}{2}-1/2\Rightarrow a=\frac{1}{\sqrt{3}-\sqrt{2}}=\sqrt{3}+\sqrt{2}\),故選\(\bbox[red,2pt]{(C)}\)。
若\(L_1//L_3\Rightarrow a=-1\);若\(L_2//L_3\Rightarrow a=3/2\);
\(L_1與L_2\)的交點\(P=(1, -1/3)\),若三線交於P點,則\(1+a/3=-2\Rightarrow a=-9\);
因此\(a=-1,3/2, -9\)符合條件,故選\(\bbox[red,2pt]{(B)}\)。
2男+6女:\(C^4_2\times C^6_6=6\)種組隊方式
3男+5女:\(C^4_3\times C^6_5=24\)種組隊方式
4男+4女:\(C^4_4\times C^6_4=15\)種組隊方式
因此共有 6+24+15=45,故選\(\bbox[red,2pt]{(A)}\)。
(A)選出3人需擔任不同職務,還需增加排列數
(B)尚需考慮正負號
(C) \(\frac{8!}{3!5!}=C^8_3\)
(D)相當求x+y+z=8的正整數解
故選\(\bbox[red,2pt]{(C)}\)。
(A)若\(\sin{\theta}>0\),\(x\)可能為負,則\(x\sin{\theta}<0\)
(B)若\(\cos{\theta}>0\),\(y\)可能為負,則\(y\cos{\theta}<0\)
(C)若\(\cot{\theta}>0\),則\(xy>0\),\(x\)可能為負,則\(x\cot{\theta}<0\)
(D)若\(\csc{\theta}>0\),則\(y>0\),\(y\csc{\theta}>0\);若\(\csc{\theta}<0\),則\(y<0\),\(y\csc{\theta}>0\);
故選\(\bbox[red,2pt]{(D)}\)。
$$\frac { \cos { B } +i\sin { B } }{ \left( \cos { A } +i\sin { A } \right) \left( \cos { C } +i\sin { C } \right) } =\frac { \cos { B } +i\sin { B } }{ \cos { \left( A+C \right) } +i\sin { \left( A+C \right) } } \\=\cos { \left( B-A-C \right) } +i\sin { \left( B-A-C \right) } \\ \Rightarrow \sin { \left( B-A-C \right) } =0\Rightarrow B-A-C=0\Rightarrow B=A+C\\\Rightarrow A+B+C=2B=180°\left( \triangle 三角和=180° \right) \Rightarrow B=90°,故選\bbox[red,2pt]{(C)}。$$
兩直線斜率相乘為-1,因此兩直線相互垂直,其圖形如上圖。由題意可知:\(\overline{AC}=26\)且\(\tan{\alpha}=\frac{2}{3},\tan{\beta}=\frac{3}{2}\)
\(\overline{BC}=\overline{AC}\sin{\alpha}=26\times \frac{2}{\sqrt{13}}=\frac{52}{\sqrt{13}}\)
同理,\(\overline{AB}=\overline{AC}\sin{\beta}=26\times \frac{3}{\sqrt{13}}=\frac{78}{\sqrt{13}}\)
因此三角形面積為\(\overline{AB}\times\overline{BC}\div 2= \frac{78}{\sqrt{13}}\times \frac{52}{\sqrt{13}}\times\frac{1}{2}=156\),故選\(\bbox[red,2pt]{(D)}\)。
由橢圓方程式可知中心坐標為(0,1)、\(a=5,b=3 \Rightarrow c=4\),因此\(F=(\pm 4,1)\),直線L即為y軸;
由拋物線方程式可知:頂點坐標為\((h,k)=(\pm 4/2,1)=(\pm 2,1), c=2\);
因此\(|chk|=|2\times \pm 2\times 1|=4\),故選\(\bbox[red,2pt]{(D)}\)。
$$由旋轉矩陣可知:\begin{bmatrix}x\\y\end{bmatrix}=\begin{bmatrix}\cos{30^\circ} & -\sin{30^\circ}\\ \sin{30^\circ} & \cos{30^\circ} \end{bmatrix} \begin{bmatrix} -3\\4\end{bmatrix}=\begin{bmatrix}\sqrt{3}/2 & -1/2\\ 1/2 & \sqrt{3}/2 \end{bmatrix} \begin{bmatrix} -3\\4\end{bmatrix}\\= \begin{bmatrix}(-3\sqrt{3}-4)/2\\(4\sqrt{3}-3)/2\end{bmatrix},故選\bbox[red,2pt]{(A)}。$$
$$f(t)=\frac{100t}{t^2+9}\Rightarrow f'(t)=\frac{100}{t^2+9}-\frac{200t^2}{(t^2+9)^2}\\
令f'(t)=0\Rightarrow 100(t^2+9)=200t^2 \Rightarrow t^2=9\Rightarrow t=3(t=-3不合),故選\bbox[red,2pt]{(C)}$$
























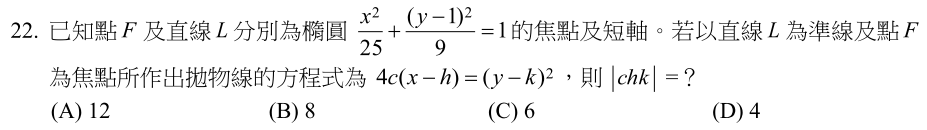



沒有留言:
張貼留言