國立科學工業園區實驗高級中學 109 學年度
第一次教師甄選-數學科試題
填充題
解：
$$987657= 3\times 329219= 3\times 11\times 29929 =3\times 11\times 173^2 \Rightarrow 最大質因數\bbox[red,2pt]{173}$$
$$五位數=abcde = a\times 10^4+ b\times 10^3+c\times 10^2 +d\times 10+e，需符合a > b > c > d > e\\ \begin{array}{} a & b & c & d & e & 數量& 小計\\\hline 4 & 3 & 2 & 1 & 0 & 1 & 1\\ 5 & - & - & - & - & C^5_4=5& 6\\ 6 & - & - & - & - & C^6_4=15& 21 \\ 7 & - & - & - & - & C^7_4= 35& 56\\\hdashline 8 & 3 & 2 & 1 & 0 & 1& 57\\8 & 4 & - & - & - & C^4_3=4& 61\\ 8 & 5 & - & - & - & C^5_3=10 & 71 \\ 8 & 6 & - & - & - & C^6_3=20& 91 \\ 8 & 7 & 2 & 1 & 0 & 1& 92 \\ 8 & 7 & 3 &- & - & C^3_2=3 & 95 \\ 8 & 7 & 4 & - & - &C^4_2=6 & 101 \\8 & 7 & 5 & - & - &C^5_2=10 & 111\\\hline \end{array}\\ \Rightarrow 第111位是87543、第110位是87542、第109位是\bbox[red,2pt]{87541}。$$
解：
$$f(x)=x^5-x^4-x^3-x^2-x-3 \Rightarrow f'(x)=5x^4-4x^3-3x^2-2x-1\\ \Rightarrow {f'(x)\over f(x)} =\sum_{k=0}^\infty { a^k+b^k+c^k +d^k +e^k\over x^{k+1}};\\ 由長除法(見上圖)可知: {f'(x)\over f(x)} = {5\over x}+ {1\over x^2}+ {3\over x^3}+ {7\over x^4}+ {15\over x^5}+ {41\over x^6}+\cdots，\\因此a^5+b^5+c^5 +d^5 +e^5= \bbox[red, 2pt]{41}\\公式來源:\href{https://web.math.sinica.edu.tw/math_media/d311/31106.pdf}{按這裡}$$
解：
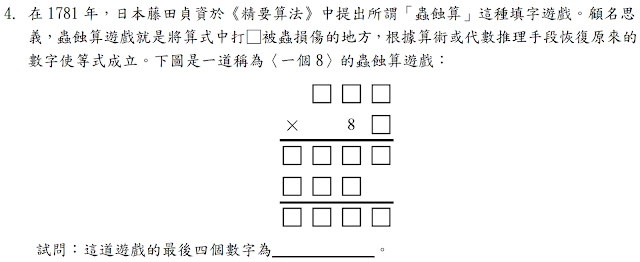
$$(a\;b\;c)\times 8 = (p\;q\;r) \Rightarrow a=1(若a \ge 2, 乘積為四位數)且b\le 2;\\又(1\;b\;c)\times d 為四位數，因此可得112\times 89=\bbox[red,2pt]{9968}$$
$$令f(x)=ax^2+bx+c，由f(x-2)= f(-x-2)\\ \Rightarrow a(x-2)^2+b(x-2)+c =a(-x-2)^2+b(-x-2)+c \\ \Rightarrow ax^2 +(b-4a)x+4a-2b+c = ax^2+(4a-b)x+4a-2b+c\\ \Rightarrow b-4a=4a-b \Rightarrow b=4a \Rightarrow f(x)=ax^2+4ax+c=a(x+2)^2+c-4a;\\在x軸截得線段長=2\sqrt 2 \Rightarrow f(x)=0的兩根為-2\pm \sqrt 2 \Rightarrow f(x)=a(x+2+\sqrt 2)(x+2-\sqrt 2);\\ 再由y截距為1，即f(0)=1 \Rightarrow a(2+\sqrt 2)(2-\sqrt 2)=1 \Rightarrow a={1\over 2}\\ \Rightarrow f(x)={1\over 2}(x+2+\sqrt 2)(x+2-\sqrt 2) = \bbox[red,2pt]{{1\over 2}x^2+2x+1}$$
解：
$$1+{1\over n^2}+{1\over (n+1)^2} = 1+{(n+1)^2+n^2 \over n^2(n+1)^2} = 1+{2n^2+2n+1 \over n^2(n+1)^2} = 1+{2n^2+2n \over n^2(n+1)^2} + { 1 \over n^2(n+1)^2} \\ =1+{2 \over n(n+1)} + { 1 \over n^2(n+1)^2} =(1+{1\over n(n+1)})^2 = (1+{1\over n }-{1\over n+1})^2\\ \Rightarrow p= \sum_{k=1}^{2019} (1+{1\over n }-{1\over n+1}) =2019+\sum_{k=1}^{2019} ({1\over n }-{1\over n+1}) =2019+1-{1\over 2020}\\ = 2020-{1\over 2020} \Rightarrow p最接近之正整數為\bbox[red, 2pt]{2020}$$
解：
$$\log_2(kx^2)+x = 2^{|x|}+x \Rightarrow \log_2(kx^2)= 2^{|x|}，而兩圖形\cases{y= \log_2(kx^2)\\ y=2^{|x|}}皆對稱y軸，\\因此兩交點可設為\cases{A(a,\log_2(ka^2)+a)\\ B(-a,\log_2(k(-a)^2)-a)}，再由\overline{AB}= \sqrt{4a^2+4a^2}=8\sqrt 2 \Rightarrow a =4 ；\\將x=a=4代回原式，可得 \log_2(k\cdot 4^2)+4 =2^{|4|}+4 \Rightarrow \log_2 (16k)=16 \Rightarrow k=\bbox[red,2pt]{4096}$$
解：
$$f(x)={7\over 3}\sqrt{9+x^2}-{2\over 3}x \Rightarrow f'(x)=0 \Rightarrow {7x \over 3\sqrt{9+x^2}} ={2\over 3} \Rightarrow 7x=2\sqrt{9+x^2} \\ \Rightarrow 49x^2=4(9+x^2) \Rightarrow 45x^2=36 \Rightarrow x=\sqrt{36\over 45}(\because x\ge 0) = {6\over 3\sqrt 5} \Rightarrow x=\bbox[red, 2pt]{2\over \sqrt 5}$$
$$令f(x)=g(x)+ax+b \Rightarrow \cases{f^2=(g+(ax+b))^2 = g^2+2(ax+b)g+(ax+b)^2 \\ g^2=(f-(ax+b))^2 = f^2-2(ax+b)f+ (ax+b)^2};\\ 又\cases{f^2除以g的餘式為4x+1\\ g^2除以f的餘式為5x+3} \Rightarrow (ax+b)^2 =\cases{a^2g(x)+4x+1 \\ a^2f(x)+5x+3 } \\ \Rightarrow a^2g(x)+4x+1=a^2f(x)+5x+3 \Rightarrow a^2(g-f)=x+2 \\\Rightarrow a^2(-ax-b)=x+2 \Rightarrow -a^3x-a^2b= x+2 \Rightarrow \cases{a=-1\\b=-2} 代回(ax+b)^2 =a^2g(x)+4x+1 \\\Rightarrow (-x-2)^2=g(x)+4x+1 \Rightarrow x^2+4x+4=g(x)+4x+1 \Rightarrow g(x) =\bbox[red,2pt]{x^2+3}$$
$$P為\overline{BD}中點\Rightarrow P((2+4)/2,(4+2)/2,0)=(3,3,0)；\\ 假設平面E與\overline{BC}交於Q點，則{四面體A-PQB體積\over 四面體A-BCD體積} ={\triangle BPQ\over \triangle BCD} ={\overline{BQ}\cdot \overline{BP} \over \overline{BC}\cdot \overline{BD}}={1\over 3}\\ \Rightarrow {\overline{BQ}\cdot \overline{BD}/2 \over 2\sqrt 5\cdot \overline{BD}}={1\over 3} \Rightarrow \overline{BQ}={4\over 3}\sqrt 5 \Rightarrow {\overline{BQ} \over \overline{BC}} = {4\sqrt 5/3\over 2\sqrt 5} ={2\over 3} \Rightarrow Q(2/3,4/3,0)\\ 因此\cases{\overrightarrow{AP} =(3,3,-1)\\ \overrightarrow{AQ}=(2/3,4/3, -1)} \Rightarrow 平面E 法向量\vec n= \overrightarrow{AP} \times \overrightarrow{AQ} =(-5/3,7/3,2) \\ \Rightarrow 平面E方程式: -{5 \over 3}x+{7\over 3}y+2(z-1)=0 \Rightarrow \bbox[red,2pt]{-5x+7y+6z=6}$$
-- END (未公告計算題題目，填充題詳解僅供參考) --
沒有留言:
張貼留言