111 學年度身心障礙學生升學大專校院甄試
甄試類(群)組別：大學組-數學 A
單選題，共 20 題，每題 5 分
解答：$$假設第二群的平均成績為a，則15(a-5)+ 30a+ 5(a+45)= 50\times 50 \\ \Rightarrow 50a=2350 \Rightarrow a=47，故選\bbox[red,2pt]{(A)}$$
解答：$$\cases{上午:數學、物理及化學三選二作為開始或結束，有2C^3_2選法，剩下3科任排，有3!排法\\ 下午:天文和森林任排，有2!=2種排法} \\ 因此共有2C^3_2\times 3!\times 2= 72種順序，故選\bbox[red,2pt]{(B)}$$
解答：$$f(x)= x^3 +ax^2 +bx-5 = (x-1)(x-2)(x-3)+k，其中k為餘式(數)\\ \Rightarrow -5=-6+k \Rightarrow k=1 \Rightarrow f(x) =(x-1)(x-2)(x-3)+1\\ \Rightarrow f(4) =3\cdot 2\cdot 1+1 =7，故選\bbox[red,2pt]{(D)}$$
解答：$$A=\begin{bmatrix} a & b\\ c& d\end{bmatrix} \Rightarrow \cases{A\begin{bmatrix}1\\ 0\end{bmatrix} =\begin{bmatrix} a & b\\ c& d\end{bmatrix} \begin{bmatrix}1\\ 0\end{bmatrix} = \begin{bmatrix}a\\ c\end{bmatrix} =\begin{bmatrix}1\\ 0\end{bmatrix} \\[1ex] A\begin{bmatrix}3\\ 2\end{bmatrix} =\begin{bmatrix} a & b\\ c& d\end{bmatrix} \begin{bmatrix}3\\ 2 \end{bmatrix} = \begin{bmatrix}3a+2b\\ 3c+2d \end{bmatrix}=\begin{bmatrix} 3\\ -2 \end{bmatrix} } \Rightarrow \cases{a=1 \\ b=0\\ c=0 \\d=-1} \\ \Rightarrow A=\begin{bmatrix} 1 & 0\\ 0 & -1\end{bmatrix} \Rightarrow A^2 \begin{bmatrix} 5\\ -4 \end{bmatrix} =\begin{bmatrix} 1 & 0\\ 0 & 1\end{bmatrix}\begin{bmatrix} 5\\ -4 \end{bmatrix} =\begin{bmatrix} 5\\ -4 \end{bmatrix} \Rightarrow \cases{p=5\\ q=-4} \Rightarrow p+q=1，故選\bbox[red,2pt]{(A)}$$
解答：$$\log_2(2^{60} \times 3\%) =60+ \log_2 {3\over 100} =60+ {\log {3\over 100} \over \log 2} =60 +{0.4771-2\over 0.301} \approx 60-5.06=54.94\\，故選\bbox[red,2pt]{(D)}$$
解答：$$\cases{\vec a的長度=1\\ (2\vec a-\vec b)\bot \vec a\\ (8\vec a-\vec b)\bot b} \Rightarrow \cases{(2\vec a-\vec b)\cdot \vec a=0 \\ (8\vec a-\vec b)\cdot \vec b =0} \Rightarrow \cases{2|\vec a|^2-\vec a\cdot \vec b=0 \cdots(1)\\ 8\vec a\cdot \vec b-|\vec b|^2=0 \cdots(2)}\\ 由(1) \Rightarrow \vec a\cdot \vec b=2|\vec a|^2 = 2代入(2) \Rightarrow 16-|\vec b|^2=0 \Rightarrow |\vec b|=4，故選\bbox[red,2pt]{(B)}$$
解答：$$\cases{O(0,0,0)\\ A(5,4,3)\\ B(a,0,0)} \Rightarrow \cases{\overrightarrow{BO} =(-a,0,0) \\ \overrightarrow{BA} =(5-a, 4 ,3)} \Rightarrow \cos \angle OBA ={\overrightarrow{BO} \cdot \overrightarrow{BA} \over |\overrightarrow{BO} ||\overrightarrow{BA} | } =\cos {\pi\over 4} \\ \Rightarrow {a^2-5a\over a\cdot \sqrt{25+(5-a)^2}} ={a-5\over \sqrt{25+(a-5)^2}} = {\sqrt 2\over 2} \Rightarrow 4(a-5)^2 = 50+2(a-5)^2 \Rightarrow (a-5)^2 = 25\\ \Rightarrow a=10(0不合，違反a\gt 0)，故選\bbox[red,2pt]{(C)}$$
解答：$$\sqrt 3+2\cos \theta\lt 0 \Rightarrow -1\le \cos \theta \lt -{\sqrt 3\over 2} \Rightarrow 1\ge \cos^2\theta \gt {3\over 4 } \Rightarrow 0\le 1-\cos^2\theta \lt {1\over 4} \\\Rightarrow 0\le \sin^2\theta \lt {1\over 4} \Rightarrow -{1\over 2 }\lt \sin \theta \lt {1\over 2} ，故選\bbox[red,2pt]{(C)}$$
解答：$$\overline{OB}邊上的高=h\Rightarrow L_1與L_2的交點A(h,h) \Rightarrow L_2為過A且斜率為-1的直線\\ \Rightarrow L: y=-(x-h)+h \Rightarrow B(2h,0) \Rightarrow \triangle OAB面積={1\over 2}\cdot \overline{OB}\cdot h= {1\over 2}\cdot 2h\cdot h= h^2=100 \\\Rightarrow h=10，故選\bbox[red,2pt]{(C)}$$
解答：$$將L代入E_1 \Rightarrow (2t+1)+2t-(t-2)=3 \Rightarrow 3t=0 \Rightarrow t=0 \Rightarrow 交點P(1,0,-2)\\將L代入E_2 \Rightarrow (2t+1)+2t-(t-2)=9 \Rightarrow 3t=6 \Rightarrow t=2 \Rightarrow 交點Q(5,4,0)\\ \Rightarrow \overline{PQ} =\sqrt{4^2 +4^2 +2^2 } =\sqrt {36}=6，故選\bbox[red,2pt]{(C)}$$
解答：$$\cases{A(2,0)\\ B(1,\sqrt 3)} \Rightarrow \overline{AB}中點 C(3/2,\sqrt 3/2); L通過O(0,0)及C(3/2,\sqrt 3/2) \Rightarrow L:y =x/\sqrt 3 \\ \Rightarrow P=(3, \sqrt 3) \Rightarrow \cases{\overrightarrow{OP} =(3,\sqrt 3)\\ \overrightarrow{OA} =(2,0)\\ \overrightarrow{OB}=(1,\sqrt 3)} \Rightarrow \overrightarrow{OP} =\overrightarrow{OA} +\overrightarrow{OB} \Rightarrow \cases{r=1\\ s=1} \Rightarrow r+s=2，故選\bbox[red,2pt]{(C)}$$
解答：
$${\triangle CAP\over \triangle CAQ} ={\overline{PB}\over \overline{QA}} ={\overline{CP}\sin \theta \over \overline{CA}\tan \theta} ={\sin \theta \over 2\tan \theta} ={1\over 2}\cos \theta，故選\bbox[red,2pt]{(B)}$$
解答：$$f(x)=3x^3+ax+b \Rightarrow f'(x)=9x^2+a \Rightarrow f''(x)=18x =0\Rightarrow x=0 \\\Rightarrow y=f(x)的對稱中心(0,f(0)) =(0,b) = (x_0,y_0)\\ (A) g(x)= 3x^3-ax-b \Rightarrow g''(x)=18x=0 \Rightarrow x=0 \Rightarrow 對稱中心(0,-b) =(x_0,-y_0)\\ (B)g(x)=x^3+ax+b \Rightarrow g''(x)=9x=0\Rightarrow x=0 \Rightarrow 對稱中心(0,b) = (x_0,y_0)\ne (3x_0,3y_0)\\(C) g(x)=3x^3+ a(x+1)+b \Rightarrow g''(x)=18x=0 \Rightarrow x=0 \Rightarrow 對稱中心(0,a+b) \ne(x_0+1,y_0)\\ (D)g(x)=3x^3-a(x-1)+b \Rightarrow g''(x) =18x=0 \Rightarrow x=0 \Rightarrow 對稱中心(0,a+b) \ne(-x_0-1,y_0)\\，故選\bbox[red,2pt]{(A)}$$
解答：$$\begin{vmatrix} a & b & c\\ 1 & 3 & 0 \\ 3 & 4 & 0\end{vmatrix} =-5c={5\over 2} \Rightarrow c=-{1\over 2} \Rightarrow \vec \omega=(a,b,c)在z軸的投影長度=|c|={1\over 2}，故選\bbox[red,2pt]{(B)}$$
解答：$$\cases{a_1=1\\ a_{n+1}=1/a_n +1,n是奇數\\ a_{n+1}=1/(a_n-1)+1,n是偶數} \Rightarrow \cases{a_{2k-1}=k\\ a_{2k}=1+1/k}, k\in \mathbb{N} \Rightarrow \cases{a_3=2\\ a_{11}=6} \Rightarrow a_{11}-a_3 =4\\，故選\bbox[red,2pt]{(C)}$$
解答：$$乙每次抽球號碼皆大於甲的情形(乙,甲)=\{(2,1),(4,2), (6,3),(8,4)\},\{(2,1),(4,2), (6,4),(8,3)\}\\,\{(2,1),(4,3), (6,2),(8,4)\},\{(2,1),(4,3), (6,4),(8,2)\},共四種情形，機率為{4\over 4!} ={1\over 6}，故選\bbox[red,2pt]{(B)}$$
解答：
$$(x,y)=(1,0),(1,1),(2,0),(2,1),(2,2), (3,1),(3,2),(3,3), (4,2), (4,3),(4,4)\\, (5,3),(5,4)，共13個整數點，故選\bbox[red,2pt]{(D)}$$
解答：$$A=(1,1) \Rightarrow \cases{B為A逆時針旋轉\alpha 角 \\ C為\sqrt 2A 逆時針旋轉\beta 角} ，又\cases{\overline{OA} =\overline{OB}=1 \\ \overline{OC}= 2\\ \vec A+\vec B+\vec C= \vec 0} \\ 其中\cases{A(1,1)\\ B(-1,1)\\ C(0,- 2)}符合以上要求，即\alpha =90^\circ，故選\bbox[red,2pt]{(D)}$$
解答：$$\cases{a^4=1.30321\times 10^5\\ a^7= 8.93871739\times 10^8} \Rightarrow \cases{\log a^4= \log(1.30321\times 10^5)\\ \log a^7= \log (8.93871739\times 10^8)} \Rightarrow \cases{4\log a= 5+\log(1.30321 )\\ 7\log a= 8+\log (8.93871739 )} \\ \Rightarrow \cases{\log a= 1.25 + {1\over 4}\log(1.30321 )\gt 1.25+{1\over 4}\log 1=1.25 \\ \log a={8\over 7}+{1\over 7}\log (8.93871739 )\lt {8\over 7}+{1\over 7}\log9 ={8\over 7}+{2\over 7}\cdot 0.4771 =1.279} \\ \Rightarrow 1.25\lt \log a\lt 1.279，故選\bbox[red,2pt]{(B)}$$
解答：$$假設各店排隊人數為(a,b,c)=(4,10,20)的排列，共有以下情形:\\ \begin{array}{rrr|c} a& b& c& 選定排隊人數\\\hline 4& 10 & 20 & 20 \\ 4 & 20 & 10 & 10\\ 10 & 4 & 20 & 4\\ 10 & 20 & 4& 4\\ 20 & 4& 10 & 4\\ 20 & 10& 4 & 10\end{array} \Rightarrow 排隊人數期望值=(20+10+4+4+4+10)\div 3! ={26\over 3}\\，故選\bbox[red,2pt]{(A)}$$
========================= END ==============================
解題僅供參考，其他歷屆試題及詳解
解答：$$f(x)=3x^3+ax+b \Rightarrow f'(x)=9x^2+a \Rightarrow f''(x)=18x =0\Rightarrow x=0 \\\Rightarrow y=f(x)的對稱中心(0,f(0)) =(0,b) = (x_0,y_0)\\ (A) g(x)= 3x^3-ax-b \Rightarrow g''(x)=18x=0 \Rightarrow x=0 \Rightarrow 對稱中心(0,-b) =(x_0,-y_0)\\ (B)g(x)=x^3+ax+b \Rightarrow g''(x)=9x=0\Rightarrow x=0 \Rightarrow 對稱中心(0,b) = (x_0,y_0)\ne (3x_0,3y_0)\\(C) g(x)=3x^3+ a(x+1)+b \Rightarrow g''(x)=18x=0 \Rightarrow x=0 \Rightarrow 對稱中心(0,a+b) \ne(x_0+1,y_0)\\ (D)g(x)=3x^3-a(x-1)+b \Rightarrow g''(x) =18x=0 \Rightarrow x=0 \Rightarrow 對稱中心(0,a+b) \ne(-x_0-1,y_0)\\，故選\bbox[red,2pt]{(A)}$$
解答：$$\begin{vmatrix} a & b & c\\ 1 & 3 & 0 \\ 3 & 4 & 0\end{vmatrix} =-5c={5\over 2} \Rightarrow c=-{1\over 2} \Rightarrow \vec \omega=(a,b,c)在z軸的投影長度=|c|={1\over 2}，故選\bbox[red,2pt]{(B)}$$
解答：$$\cases{a_1=1\\ a_{n+1}=1/a_n +1,n是奇數\\ a_{n+1}=1/(a_n-1)+1,n是偶數} \Rightarrow \cases{a_{2k-1}=k\\ a_{2k}=1+1/k}, k\in \mathbb{N} \Rightarrow \cases{a_3=2\\ a_{11}=6} \Rightarrow a_{11}-a_3 =4\\，故選\bbox[red,2pt]{(C)}$$
解答：$$乙每次抽球號碼皆大於甲的情形(乙,甲)=\{(2,1),(4,2), (6,3),(8,4)\},\{(2,1),(4,2), (6,4),(8,3)\}\\,\{(2,1),(4,3), (6,2),(8,4)\},\{(2,1),(4,3), (6,4),(8,2)\},共四種情形，機率為{4\over 4!} ={1\over 6}，故選\bbox[red,2pt]{(B)}$$
解答：
解答：$$A=(1,1) \Rightarrow \cases{B為A逆時針旋轉\alpha 角 \\ C為\sqrt 2A 逆時針旋轉\beta 角} ，又\cases{\overline{OA} =\overline{OB}=1 \\ \overline{OC}= 2\\ \vec A+\vec B+\vec C= \vec 0} \\ 其中\cases{A(1,1)\\ B(-1,1)\\ C(0,- 2)}符合以上要求，即\alpha =90^\circ，故選\bbox[red,2pt]{(D)}$$
解答：$$\cases{a^4=1.30321\times 10^5\\ a^7= 8.93871739\times 10^8} \Rightarrow \cases{\log a^4= \log(1.30321\times 10^5)\\ \log a^7= \log (8.93871739\times 10^8)} \Rightarrow \cases{4\log a= 5+\log(1.30321 )\\ 7\log a= 8+\log (8.93871739 )} \\ \Rightarrow \cases{\log a= 1.25 + {1\over 4}\log(1.30321 )\gt 1.25+{1\over 4}\log 1=1.25 \\ \log a={8\over 7}+{1\over 7}\log (8.93871739 )\lt {8\over 7}+{1\over 7}\log9 ={8\over 7}+{2\over 7}\cdot 0.4771 =1.279} \\ \Rightarrow 1.25\lt \log a\lt 1.279，故選\bbox[red,2pt]{(B)}$$
解答：$$假設各店排隊人數為(a,b,c)=(4,10,20)的排列，共有以下情形:\\ \begin{array}{rrr|c} a& b& c& 選定排隊人數\\\hline 4& 10 & 20 & 20 \\ 4 & 20 & 10 & 10\\ 10 & 4 & 20 & 4\\ 10 & 20 & 4& 4\\ 20 & 4& 10 & 4\\ 20 & 10& 4 & 10\end{array} \Rightarrow 排隊人數期望值=(20+10+4+4+4+10)\div 3! ={26\over 3}\\，故選\bbox[red,2pt]{(A)}$$
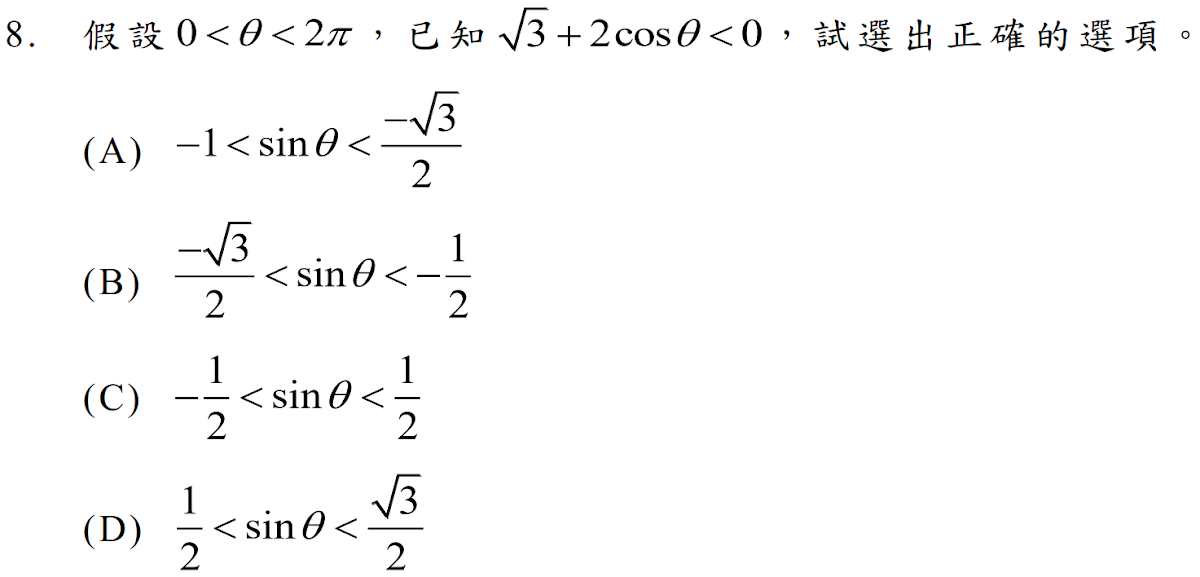
沒有留言:
張貼留言