108 年度全國科學班聯合學科資格考試 數學科
一、 單一選擇題：
解答：$$\cases{A(3,3,0)\\ B(3,0,3)\\ C(0,3,3)} \Rightarrow 包含\triangle ABC的平面E:x+y+z=6\\ \Rightarrow \cases{d(P(4,5,6),E) = 9/\sqrt 6\\ d(Q(13,-14,15),E)=8/\sqrt 6\\ d(R(\log_2(1/3),\log_3 1,\log_4 (1/5)),E)= (6+\log_2 3\sqrt 5)/ \sqrt 3} \\ \Rightarrow d(P,E)\gt d(R,E) \gt d(Q,E) \Rightarrow p\gt r\gt q，故選\bbox[red,2pt]{(4)}$$
解答：$$(1)\times: \cases{\Gamma_1:{x^2/4-y^2/9=1} \Rightarrow 貫軸長為2\cdot 2=4\\ x^2/4-y^2/9=t \Rightarrow 貫軸長為2\cdot 2\sqrt t=4\sqrt t} \Rightarrow 4\sqrt t/4 = \sqrt t \ne t \\ (2)\times: \cases{\Gamma_1:為左右形，焦點在x軸上\\ 橢圓為上下形，焦點在y軸上} \Rightarrow 兩者不同\\(3)\bigcirc: {a^2b^2\over a^2+b^2} ={4\times 9\over 4+9} ={36\over 13}\\(4)\times: |\overline{PF_1}-\overline{PF_2}|= 4 \Rightarrow \overline{PF_1}-\overline{PF_2}=\pm 4\\(5)\times: 相同的漸近線可決定多組的雙曲線，不一定剛好是\Gamma_1的共軛雙曲線\\故選\bbox[red,2pt]{(3)}$$
二、 多重選擇題：
解答：$$(1)\times: y=f(x)與y軸有交點(0,0) \Rightarrow y軸不是漸近線 \\(2)\bigcirc: f(-x)=f(-x)= \log_{10}\sqrt{x^2+1} \\(3)\bigcirc: x^2 \ge 0 \Rightarrow \log_{10} \sqrt{x^2+1 } \ge 0 \Rightarrow f(x)的最小值為0\\(4)\times: f(\cot 50^\circ) = \log_{10} \sqrt{\cot^2 50^\circ +1} =\log_{10} \csc 50^\circ \lt \log_{10} \csc 45^\circ = \log_{10}\sqrt 2\\\qquad = {1\over 2}\cdot 0.301 = 0.1505 \not \gt 0.16 \\(5) \bigcirc: f(3)= \log_{10}\sqrt{10} ={1\over 2}\in \mathbb{Q} \\故選\bbox[red,2pt]{(235)}$$
解答：$$X\sim B(n,p) \Rightarrow 期望值EX=np\\ 由圖形可知 p\approx 0.2 (中間最高值)，EX=5(中間最高的橫座標) \Rightarrow np=5 \Rightarrow n=5\div 0.2=25\\ \Rightarrow X\sim B(25,0.2)，故選\bbox[red,2pt]{(45)}$$
解答：$$z^6 +z^4+z^2+1 =0 \Rightarrow (z^2-1)(z^6 +z^4+z^2+1) =0 \Rightarrow z^8=1 \\ \Rightarrow \cases{z^8=1的8個根分別為 \cos{k\over 4}\pi +i\sin{k\over 4}\pi ,k=0-7\\ z^2=1的2個根分別為 \cos k\pi+i\sin k\pi, k=0,1} \\ \Rightarrow z^6 +z^4+z^2+1 =0 的6根分別為 z_k =\begin{cases} \cos{k\over 4}\pi +i\sin{k\over 4}\pi &k=1-3\\ \cos{(k+1)\over 4}\pi +i\sin{(k+1)\over 4}\pi &k=4-6\end{cases}\\ \Rightarrow z_1={1\over \sqrt 2} +{1\over \sqrt 2}i,z_2 =i,z_3= -{1\over \sqrt 2} +{1\over \sqrt 2}i, z_4= -{1\over \sqrt 2} -{1\over \sqrt 2}i,z_5=-i, z_6={1\over \sqrt 2} -{1\over \sqrt 2}i \\\Rightarrow \cases{\langle a_k\rangle = {1\over \sqrt 2},0,-{1\over \sqrt 2},-{1\over \sqrt 2},0,{1\over \sqrt 2}\\ \langle b_k \rangle = {1\over \sqrt 2},1,{1\over \sqrt 2},-{1\over \sqrt 2}, -1,-{1\over \sqrt 2}} \Rightarrow S=\{{4\over \sqrt 2}, 1, -{2\over \sqrt 2},-{4\over \sqrt 2},-1,{2\over \sqrt 2} \}\\(1)\bigcirc: 六根皆有虛數\\(2) \times: 1是有理數\\(3)\times: 虛數無大小 \\(4) \times: z_2=i \Rightarrow i\cdot z_2= -1 =c_2+d_2i \Rightarrow \cases{c_2=-1\\ d_2= 0} \Rightarrow 3c_2+d_2= -3 \not \in S \\(5)\bigcirc: z_4= -{1\over \sqrt 2} -{1\over \sqrt 2}i \Rightarrow i\cdot z_4= {1\over \sqrt 2} -{1\over \sqrt 2}i \Rightarrow \cases{c_4=1/\sqrt 2\\ d_4=-1/\sqrt 2} \Rightarrow 3c_4+d_4 = 2/\sqrt 2 \in S\\ 故選\bbox[red, 2pt]{(15)}$$
三、 填充題：（每題 5 分）
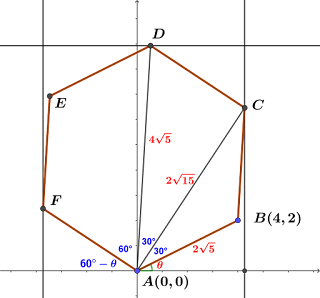
解答：
$$\cases{\overline{PB} =8\\ \overline{PC}=6 \\ \overline{BC}=10 } \Rightarrow \overline{BC}^2 =\overline{PB}^2 +\overline{PC}^2 \Rightarrow \angle BPC=90^\circ; \\取Q在\overline{BC}上且\overline{BC} \bot \overline{PQ} \Rightarrow \overline{PB}\cdot \overline{PC} =\overline{BC}\cdot \overline{PQ} \Rightarrow \overline{PQ} = 8\times 6\div 10= {24\over 5} \\ \Rightarrow \overline{BQ}= \sqrt{8^2-(24/5)^2} ={32\over 5}\\ 因此假設\cases{B(0,0) \\C(10,0)} \Rightarrow \cases{A(5,12)\\ P(32/5,24/5)} \Rightarrow \cases{\vec u= \overrightarrow{AB}=(-5,-12)\\ \vec v= \overrightarrow{AP}= (7/5, -36/5)\\ \vec w= \overrightarrow{AC}=(5,-12) } \Rightarrow \cases{|\vec u|=13\\ |\vec v|= \sqrt{269/5}\\ |\vec w|=13 \\ \vec u\cdot \vec v= 397/5\\ \vec v\cdot \vec w= 467/5}\\ \Rightarrow \cases{\triangle PAB = {1\over 2} \sqrt{|\vec u|^2|\vec v|^2 -(\vec u\cdot \vec v)^2} \\\triangle PAC = {1\over 2} \sqrt{|\vec v|^2|\vec w|^2 -(\vec v\cdot \vec w)^2}} \Rightarrow {\triangle PAB\over \triangle PAC} =\sqrt{ |\vec u|^2|\vec v|^2 -(\vec u\cdot \vec v)^2\over |\vec v|^2|\vec w|^2 -(\vec v\cdot \vec w)^2} =\sqrt{121\over 16} =\bbox[red,2pt]{11\over 4}$$
$$\cases{A(0,0)\\ B(4,2)} \Rightarrow 邊長d=\overline{AB} = 2\sqrt 5 \Rightarrow \cases{2\sqrt 5\cos \theta=4\\ 2\sqrt 5\sin \theta = 2} \Rightarrow \cases{\cos \theta =2/\sqrt 5\\ \sin \theta =1/\sqrt 5}\\ 又d=2\sqrt 5 \Rightarrow \cases{\overline{AD} =2d = 4\sqrt 5\\ \overline{AC} = \sqrt 3 d=2\sqrt{15} \\ \overline{AF}=d=2\sqrt 5} \Rightarrow \cases{D(4\sqrt 5\cos(60^\circ +\theta), 4\sqrt 5\sin (60^\circ+\theta)) \\C(2\sqrt{15} \cos(30^\circ +\theta), 2\sqrt{15} \sin(30^\circ +\theta)) \\F(-2\sqrt 5 \cos(60^\circ-\theta), 2\sqrt 5 \sin(60^\circ-\theta)} \\ \Rightarrow \cases{D(4-2\sqrt 3,2+4\sqrt 3)\\ C(6-\sqrt 3,3+2\sqrt 3) \\F(-2- \sqrt 3, 2\sqrt 3-1)} \Rightarrow 矩形面積= (6-\sqrt 3+2+\sqrt 3)\times (2+4\sqrt 3) = \bbox[red,2pt]{16 +32\sqrt 3}$$
$$此題相當於求兩圖形\cases{\Gamma_1:y=|2x+3| \\ \Gamma_2: y =x^2+4x+k}有四個交點時，k的範圍?\\當\Gamma_1的頂點(-3/2,0)在\Gamma_2時，0={9\over 4}-6+k \Rightarrow k={15\over 4}\\ 當y=2x+3與\Gamma_2相切:x^2+4x+k=2x+3 \Rightarrow x^2+2x+k-3=0 的判別式為0 \\ \Rightarrow 4-4(k-3)=0 \Rightarrow k=4\\ 因此當\bbox[red,2pt]{{15\over 4} \lt k \lt 4}時，兩圖形有四個交點$$
$$假設A、C在\overline{BD}上的垂足分別為E、F，見上圖；\\ \overline{BD} =\sqrt{\overline{AB}^2 +\overline{AD}^2} =\sqrt{4+1} =\sqrt 5；又\overline{BD}\times \overline{AE}= \overline{AB}\times \overline{AD} \Rightarrow \overline{AE}={2\over \sqrt 5}\\ 因此\overline{DE} =\sqrt{\overline{AD}^2 -\overline{AE}^2} = {1\over \sqrt 5}\\ 令E為空間中的原點，則\cases{E(0,0,0)\\ F(\sqrt 5-{2\over \sqrt 5},0,0)\\ C(\sqrt 5-{2\over \sqrt 5},-{2\over \sqrt 5},0)}；\\ 而旋轉後的A點坐標(0,\overline{AE} \cos 60^\circ ,\overline{AE} \sin 60^\circ) =(0,{1\over \sqrt 5}, \sqrt{3\over 5})\\ 因此\overline{AC}= \sqrt{ \left( \sqrt 5-{2\over \sqrt 5} \right)^2 +\left({3\over \sqrt 5}\right)^2 +\left(\sqrt{3\over 5}\right)^2} = \sqrt{21\over 5} = \bbox[red, 2pt]{\sqrt{105}\over 5}$$
解答：$$擲2次就停止:第1次有6種可能，第2次與第1次需相同，因此共有6\times 1=6種可能;\\擲3次就停止:第1次有6種可能、第2次有5種可能，第3次需與第2次相同，因此共有6\times 5\times 1=30種可能;\\擲4次就停止:有6\times 5\times 5\times 1=150種可能\\擲5次就停止:6\times 5\times 5\times 5\times 6=4500\\ 因此總共有6+30+120+ 2160= \bbox[red, 2pt]{4686}種可能$$
三、 計算與證明：（每題 8 分）
解答：$$兩圖形\cases{L:y=mx+n \\ \Gamma:y=f(x)} 有相異三交點 \Rightarrow f(x)-mx-n=0 的三個根為a,b,c\\ \Rightarrow f(x)-mx-n = k(x-a)(x-b)(x-c) \Rightarrow f(x)= k(x-a)(x-b)(x-c)+mx +n\\ \Rightarrow f(x)= k(x^3-(a+b+c)x^2 +(ab+bc+ca)x -abc)+mx+n\\ \Rightarrow f'(x)=k(3x^2-2(a+b+c)x+ ab+bc+ca)+m\\ \Rightarrow f''(x)=k(6x-2(a+b+c))\\ 因此f''(x)= 0 \Rightarrow x={2\over 6}(a+b+c) ={a+b +c\over 3} \Rightarrow 反曲點為\left({a+b +c\over 3},({a+b +c\over 3}) \right)，\bbox[red, 2pt]{故得證}$$
解答：
$$假設此拋物線的準線為L，A在L的垂足為A'、B在L的垂足為B'；\\ 另L'\parallel L，且L'經過拋物線焦點F，L'與\overline{AA'}的交點為C、與\overline{BB'}的交點為D，如上圖；\\ \cases{\overline{AF}=10\\ \overline{BF}=5 \\ \overline{AB} =5\sqrt 5} \Rightarrow \overline{AB}^2 =\overline{AF}^2 +\overline{BF}^2 \Rightarrow \angle AFB=90^\circ\\ \angle AFC+ \angle BFD = 90^\circ = \angle BFD+\angle DBF \Rightarrow \angle AFC=\angle DBF =\theta\\ 由拋物線定義可知:\cases{\overline{AF} =10= \overline{AA'} =10\sin \theta+2c\\ \overline{BF}=5 = \overline{BB'} =5\cos \theta+2c} \Rightarrow 10-10\sin\theta =5-5\cos \theta\\ \Rightarrow \cos\theta = 2\sin \theta -1 \Rightarrow (2\sin\theta-1)^2 +\sin^2\theta =1 \Rightarrow 5\sin^2\theta -4\sin\theta=0 \Rightarrow \sin\theta =4/5\\ \Rightarrow 10=10\cdot {4\over 5}+2c \Rightarrow 2c=2 \Rightarrow c=1 \Rightarrow 正焦弦長=4|c|= \bbox[red,2pt]{4}$$
$$圓C向右平移2單位成為圓C':(x-3)^2+ (y-2)^2=8，又L':y=m(x+3) \Rightarrow mx-y+3m=0\\ L'與圓C'相切，也就是d((3,2),L')=\sqrt 8 \Rightarrow \left|{ 3m-2+3m\over \sqrt{m^2+1}} \right| =\sqrt 8 \Rightarrow {(6m-2)^2\over m^2+1} =8\\ \Rightarrow 7m^2-6m-1=0 \Rightarrow (7m+1)(m-1)=0 \\\Rightarrow \cases{m=1 \Rightarrow L':y=x+3 切點為B(1,4) \\ m=-1/7 \Rightarrow L':x+7y+3=0切點為B'(13/5,-4/5)}\\ B'在直線x=2的右邊，因此B'不在對摺後的圓周上，也就是m=-1/7不合\\也就是L':\bbox[red,2pt]{y=x+3} \\ \bbox[blue,2pt]{註}:公布的答案包含x+7y=3$$
解答：
解答：$$(1)f(x)=\log_2 (x+k) \Rightarrow \cases{f(0)=\log_2 k\\ f(2)=\log_2 (k+2) \\ f(6)=\log_2(k+6)} \Rightarrow 2f(2)= f(0)+ f(6) \\\Rightarrow 2\log_2(k+2) = \log_2 k+\log_2 (k+6) \Rightarrow \log_2 (k+2)^2 = \log_2 k(k+6) \Rightarrow (k+2)^2 = k(k+6)\\ \Rightarrow 2k=4 \Rightarrow \bbox[red,2pt]{k=2}\\(2)\;a,b,c成等比\Rightarrow b^2=ac \Rightarrow f(a)+ f(c)= \log_2(a+2) +\log_2 (c+2) =\log_2 (a+2)(c+2)\\ =\log_2 (ac+ 2(a+c)+4) =\log_2(b^2+ 2(a+c)+4) \gt \log_2 (b^2+4b+4)(註) = \log_2(b+2)^2=2f(b)\\ \Rightarrow f(b)+f(c) \gt 2f(b)，\bbox[red,2pt]{故得證}\\(註:a+c \gt 2\sqrt{ac}=2b)$$
四、 數學寫作能力題： (每題 5 分， 共計 10 分)
解答：$$(1)X\sim B(n,p) \Rightarrow P(X=x) = \bbox[red,2pt]{C^n_x p^x(1-p)^{n-x},x=0,1,\dots, n} \\(2)期望值EX= \sum_{x=0}^n x C^n_x p^x(1-p)^{n-x} = \sum_{x=0}^n x \cdot {n!\over x!\cdot (n-x)!} (1-p)^n \left({p\over 1-p}\right)^x \\= (1-p)^n \sum_{x=1}^n {n\cdot (n-1)!\over (x-1)!\cdot (n-x)!} \left({p\over 1-p}\right)^x = n(1-p)^n \left({p\over 1-p}\right)\sum_{x=1}^n { (n-1)!\over (x-1)!\cdot (n-x)!} \left({p\over 1-p}\right)^{x-1} \\ = n(1-p)^n \left({p\over 1-p}\right)\sum_{x=1}^n C^{n-1}_{x-1} \left({p\over 1-p}\right)^{x-1} = n(1-p)^n \left({p\over 1-p}\right)\sum_{k=0}^n C^{n-1}_{k} \left({p\over 1-p}\right)^{k} \\ =n(1-p)^n \left({p\over 1-p}\right)\left(1+{p\over 1-p}\right)^{n-1} =n(1-p)^{n-1}p \left({1 \over 1-p}\right)^{n-1} =\bbox[red,2pt]{np}$$
解答：$$(1)A= \bbox[red, 2pt]{\begin{bmatrix}\cos 2\theta & \sin 2\theta \\ \sin 2\theta & -\cos 2\theta \end{bmatrix}}\\(2)假設\cases{P(x,y) \\P'(x',y')} 且\overline{OP}與x軸的夾角為\alpha，則L與\overline{OP}的夾角為\theta-\alpha \Rightarrow L與\overline{OP'}的夾角為\theta-\alpha \\ \Rightarrow \overline{OP}與\overline{OP'}的夾角為2(\theta-\alpha) \Rightarrow \overline{OP'}與x軸的夾角為2(\theta-\alpha)+\alpha = 2\theta -\alpha \\ \Rightarrow \cases{(x,y)= (\overline{OP}\cos \alpha, \overline{OP}\sin \alpha) \\ (x',y')= (\overline{OP'}\cos(2\theta-\alpha), \overline{OP'}\sin(2\theta-\alpha))} ，由於 \overline{OP}=\overline{OP'} \\ \Rightarrow \cases{x'=\overline{OP}\cos(2\theta-\alpha) =\overline{OP} \cos 2\theta \cos \alpha +\overline{OP} \sin 2\theta \sin \alpha =x\cos 2\theta+ y\sin 2\theta\\ y'=\overline{OP}\sin(2\theta-\alpha)= \overline{OP}\sin 2\theta \cos \alpha -\overline{OP}\sin \alpha \cos 2\theta =x \sin 2\theta-y\cos 2\theta} \\ \Rightarrow \begin{bmatrix}x' \\ y'\end{bmatrix} =\begin{bmatrix}\cos 2\theta & \sin 2\theta \\ \sin 2\theta & -\cos 2\theta \end{bmatrix} \begin{bmatrix}x \\ y\end{bmatrix} \Rightarrow A\begin{bmatrix}x \\ y\end{bmatrix} =\begin{bmatrix}x' \\ y' \end{bmatrix}，\bbox[red, 2pt]{故得證}$$
======================== END ============================
解題僅供參考
沒有留言:
張貼留言