111學年度高級中等以上學校運動成績優良學生
升學輔導甄試學科考試數學科試題
解答:$$a=0.\overline{36} =0.363636\cdots \Rightarrow 100a=36.363636\cdots \Rightarrow 100a=36+a \Rightarrow 99a=36\\ \Rightarrow a={36\over 99} ={4\over 11},故選\bbox[red,2pt]{(D)}$$解答:$$-2\le x\le 3 \Rightarrow x=-2,-1,0,1,2,3,共六個整數,故選\bbox[red,2pt]{(C)}$$
解答:$$(\sqrt 2+1)^2 =(\sqrt 3)^2 +(\sqrt{2x})^2 \Rightarrow 3+2\sqrt 2= 3+2x \Rightarrow x=\sqrt 2,故選\bbox[red,2pt]{(A)}$$
解答:$$27^{-{2\over 3}} =(3^3)^{-{2\over 3}} =3^{-2} ={1 \over 9},故選\bbox[red,2pt]{(E)}$$
解答:$$\log 16= \log 2^4 =4\log 2 =4x,故選\bbox[red,2pt]{(B)}$$
解答:$$f(x)=(x+2)p(x)+3 \Rightarrow f(-2)=0+3= 3,故選\bbox[red,2pt]{(B)}$$
解答:$$圖形為凹向上,因此a\gt 0,故選\bbox[red,2pt]{(A)}$$
解答:$$f(x)=(x-1)^3-(x-1)+1 \Rightarrow f'(x)=3(x-1)^2-1 \Rightarrow f''(x)=6(x-1)\\ 因此,若f''(x)=0,則x=1 \Rightarrow 對稱中心坐標為(1,f(1))= (1,1),故選\bbox[red,2pt]{(C)}$$
解答:$$f(x)=(x+1)^3-6(x+1)^2+ 11(x+1)-5 \Rightarrow f'(x)=3(x+1)^2-12(x+1)+11\\ 一次近似即切線,而切線斜率f'(-1)=11且切線經過(-1,f(-1)) = (-1,-5) \\\Rightarrow 切線方程式: y+5=11(x+1) \Rightarrow y = 11x+6 ,故選\bbox[red,2pt]{(D)}$$
解答:$$圖形為凹向上,即首項係數為正值;圖形恆在x軸上方代表無解,即判別式小於0,故選\bbox[red,2pt]{(E)}$$
解答:$$L:3x-y+2=0 \Rightarrow 斜率為3 \Rightarrow L'斜率為-{1\over 3},故選\bbox[red,2pt]{(A)}$$
解答:$$將各點代入,判斷是否符合x-2y+1\le 0;將(1,2)代入可得 1-4+1=-2 \lt 0,符合要求\\,故選\bbox[red,2pt]{(D)}$$
解答:$$(-1,k)至3x+4y+3 =0的距離為\left|{-3+4k+3\over \sqrt{3^2+4^2}} \right| ={|4k|\over 5} =4 \Rightarrow k=5,故選\bbox[red,2pt]{(C)}$$
解答:$$(x-2)^2+(y+1)^2=5 \Rightarrow \cases{圓心O(2,-1)\\ 圓半徑r=\sqrt 5} \Rightarrow \overline{OP} =\sqrt{(3-2)^2 +(2+1)^2} = \sqrt{10} \gt \sqrt 5\\ \Rightarrow P在圓外,故選\bbox[red,2pt]{(E)}$$
解答:$$x^2+y^2=9 \Rightarrow \cases{圓心(0,0)\\ 半徑r=3} \Rightarrow 被x軸所截線段長=直徑= 2r=6,故選\bbox[red,2pt]{(B)}$$
解答:$$a_{n+1}=3+a_n \Rightarrow a_{n+1}-a_n= 3 \Rightarrow \langle a_n\rangle 為一等差數列,公差為3,故選\bbox[red,2pt]{(A)}$$
解答:$$\cases{a_1=1\\ a_2=a_1r = r\\ a_3= a_1r^2 = r^2} \Rightarrow a_2+a_3 = r+r^2=6 \Rightarrow r^2+r-6=0 \Rightarrow (r+3)(r-2) =0\\ \Rightarrow r=2,故選\bbox[red,2pt]{(B)}$$
解答:$$30\times 60\% =18 \Rightarrow P_{60}位於第18與第19之間,即73與75之間,故選\bbox[red,2pt]{(D)}$$

解答:$$迴歸直線必過(\mu_x,\mu_y)=(3,4),故選\bbox[red,2pt]{(E)}$$
解答:$$\lfloor {200\over 3}\rfloor =66,故選\bbox[red,2pt]{(C)}$$
解答:$$只有甲乙丙丁或甲丙乙丁兩種情形,故選\bbox[red,2pt]{(B)}$$
解答:$$點數相同有6種情形,因此機率={6\over 6\times 6}={1\over 6},故選\bbox[red,2pt]{(E)}$$
解答:$$6\times{1\over 2}+2\times {1\over 2}= 4,故選\bbox[red,2pt]{(A)}$$
解答:$$P(-3,4) \Rightarrow \overline{OP}=\sqrt {3^2+4^2}=5 \Rightarrow \cos \theta =-{3\over 5} ,故選\bbox[red,2pt]{(C)}$$
解答:$$\sin 210^\circ =\sin (180^\circ +30^\circ) = -\sin 30^\circ =-{1\over 2},故選\bbox[red,2pt]{(D)}$$
解答:$$餘弦定理: \cos \angle B=\cfrac{\overline{AB}^2 +\overline{BC}^2 -\overline{AC}^2}{2\cdot \overline{AB}\cdot \overline{BC}} \Rightarrow \cos 60^\circ ={1\over 2}={25+64-\overline{AC}^2 \over 80} \Rightarrow \overline{AC}^2 = 49 \\ \Rightarrow \overline{AC}=7,故選\bbox[red,2pt]{(B)}$$
解答:$$4^2\pi \cdot {120^\circ \over 360^\circ}={16\pi\over 3},故選\bbox[red,2pt]{(A)}$$
解答:$$\sin x的週期為2\pi \Rightarrow \sin 3x週期為{2\pi \over 3},故選\bbox[red,2pt]{(C)}$$
解答:$$(E) \log_2 25= \log_2 5^2 = 2\log_2 5,故選\bbox[red,2pt]{(E)}$$
解答:$$\cases{P(1,3)\\ R(a,b)} \Rightarrow \overrightarrow{PR} =(a-1,b-3)= (-2,5) \Rightarrow \cases{a=-1\\ b=8} \Rightarrow R(-1,8),故選\bbox[red,2pt]{(D)}$$
解答:$$y=\log_3 x \;圖形特徵:\cases{遞增\\ 通過(1,0)\\ x\gt 0},故選\bbox[red,2pt]{(D)}$$
解答:$$\cases{\vec a=(1,2)\\ \vec b=(-3,4)} \Rightarrow \vec a\cdot \vec b= 1\times (-3)+2\times 4=5,故選\bbox[red,2pt]{(C)}$$
解答:$$組合後,C與E相鄰 \Rightarrow \overline{CE}=1,故選\bbox[red,2pt]{(A)}$$
解答:$$(x,y,z) \xrightarrow{xy平面對稱坐標} (x,y,-z) \Rightarrow (1,2,3)\to (1,2,-3),故選\bbox[red,2pt]{(E)}$$
解答:$$\cases{X =\left[\begin{matrix}1 & 2\\3 & 4\end{matrix}\right] \\[1ex]Y=\left[\begin{matrix}5 & 6\\7 & 8\end{matrix} \right] } \Rightarrow 2X-Y=\left[\begin{matrix}2-5 & 4-6\\6-7 & 8-8\end{matrix}\right] =\left[\begin{matrix}-3 & -2\\-1 & 0 \end{matrix}\right]=\left[\begin{matrix}a & b\\c & d\end{matrix}\right] \Rightarrow c=-1,故選\bbox[red,2pt]{(B)}$$
解答:$$\left[\begin{matrix}4\\3\end{matrix}\right]\left[\begin{matrix}6 & 5\end{matrix}\right] =\left[\begin{matrix}24 & 20\\18 & 15\end{matrix}\right] =\left[\begin{matrix}x & y\\z & w\end{matrix}\right] \Rightarrow y=20,故選\bbox[red,2pt]{(D)}$$
解答:$$A=\begin{bmatrix} 5 & 2\\ 3 & 1\end{bmatrix} \Rightarrow \det(A)=-1 \Rightarrow A^{-1}=\begin{bmatrix} -1 & 2\\ 3 & -5\end{bmatrix} =\begin{bmatrix} s & t\\ u & v\end{bmatrix} \Rightarrow s=-1,故選\bbox[red,2pt]{(A)}$$
解答:$$A、B為獨立事件\Rightarrow P(A\cap B)= P(A)P(B) = {1\over 3}\times{1\over 2} = {1\over 6},故選\bbox[red,2pt]{(E)}$$
解答:$${20\%\over 50\%} =0.4,故選\bbox[red,2pt]{(C)}$$
解答:$${男性抽菸人數\over 男性抽菸人數+女性抽菸人數} ={60\%\times 30\% \over 60\%\times 30\%+ 40\%10\%} = {0.18\over 0.18+0.04} ={9\over 11} =81.8\%\\,故選\bbox[red,2pt]{(B)}$$
=================== END =====================

























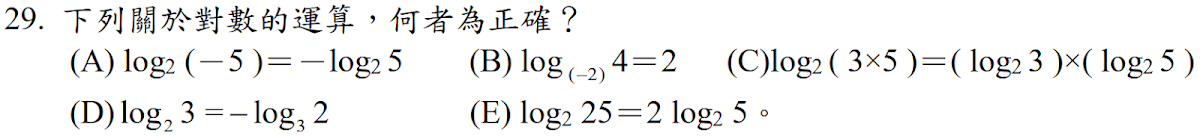











沒有留言:
張貼留言