臺中市立文華高級中等學校 112 學年度第 2 次教師甄選
一、填充題:(共 80 分)
Ⅰ.填充一(每格 4 分,共 32 分,全對才給分。)
$$P=L_1\cap L_2 = (6,9),依題意:\cases{\angle ABP=90^\circ\\ \angle ACP=90^\circ} \Rightarrow \overline{AP}=5=外接圓直徑\\ \Rightarrow 外接圓半徑=\bbox[red,2pt]{5\over 2} $$
解答:$$\cases{L_1:{x+1\over 2}={y-2\over -2}=-z\\ L_2:x-3={y-1\over -4}=z-1} \Rightarrow \cases{L_1方向向量\vec u=(2,-2,-1)\\ L_2方向向量\vec v=(1,-4,1)} \Rightarrow \cases{含L_1的平面E_1:2x+y+2z=0\\ 含L_2的平面E_2:2x+y+2z=9}\\ \Rightarrow d(E_1,E_2)={9\over \sqrt {4+1+4}}=3 \Rightarrow \overrightarrow{PQ}\cdot \overrightarrow{AB} =|\overrightarrow{PQ}|^2= (d(E_1,E_2))^2=\bbox[red, 2pt]9$$
解答:$$令5^x=y \Rightarrow x=\log_5 y \Rightarrow f(y)=7\log_5y\cdot \log_3 5+5=7\log_3 y+5\\ \Rightarrow f(3)+f(3^2)+\cdots +f(3^{10}) = \sum_{k=1}^{10}(7k+5) =7\cdot 55+50=\bbox[red, 2pt]{435}$$
解答:$$\cases{A(2,0)\\ B(-2,0)\\ P(x,y)} \Rightarrow \triangle PAB面積={1\over 2}\overline{AB}\cdot |y|=2|y|=4 \Rightarrow |y|=2 \Rightarrow y^2=4\\ \Rightarrow \triangle PAB 周長=\sqrt{(x-2)^2+y^2}+\sqrt{(x+2)^2+y^2} +4=10 \Rightarrow \sqrt{(x-2)^2+4}+\sqrt{(x+2)^2+4} =6 \\ \Rightarrow (x-2)^2+4=36+(x+2)^2+4-12\sqrt{(x+2)^2+4} \Rightarrow 2x+9=3\sqrt{(x+2)^2+4}\\ \Rightarrow 5x^2= 9 \Rightarrow x^2={9\over 5} \Rightarrow x^2+y^2={9\over 5}+4 =\bbox[red, 2pt]{29\over 5}$$
解答:
解答:$$\cases{L_1:{x+1\over 2}={y-2\over -2}=-z\\ L_2:x-3={y-1\over -4}=z-1} \Rightarrow \cases{L_1方向向量\vec u=(2,-2,-1)\\ L_2方向向量\vec v=(1,-4,1)} \Rightarrow \cases{含L_1的平面E_1:2x+y+2z=0\\ 含L_2的平面E_2:2x+y+2z=9}\\ \Rightarrow d(E_1,E_2)={9\over \sqrt {4+1+4}}=3 \Rightarrow \overrightarrow{PQ}\cdot \overrightarrow{AB} =|\overrightarrow{PQ}|^2= (d(E_1,E_2))^2=\bbox[red, 2pt]9$$
解答:$$令5^x=y \Rightarrow x=\log_5 y \Rightarrow f(y)=7\log_5y\cdot \log_3 5+5=7\log_3 y+5\\ \Rightarrow f(3)+f(3^2)+\cdots +f(3^{10}) = \sum_{k=1}^{10}(7k+5) =7\cdot 55+50=\bbox[red, 2pt]{435}$$
解答:$$\cases{A(2,0)\\ B(-2,0)\\ P(x,y)} \Rightarrow \triangle PAB面積={1\over 2}\overline{AB}\cdot |y|=2|y|=4 \Rightarrow |y|=2 \Rightarrow y^2=4\\ \Rightarrow \triangle PAB 周長=\sqrt{(x-2)^2+y^2}+\sqrt{(x+2)^2+y^2} +4=10 \Rightarrow \sqrt{(x-2)^2+4}+\sqrt{(x+2)^2+4} =6 \\ \Rightarrow (x-2)^2+4=36+(x+2)^2+4-12\sqrt{(x+2)^2+4} \Rightarrow 2x+9=3\sqrt{(x+2)^2+4}\\ \Rightarrow 5x^2= 9 \Rightarrow x^2={9\over 5} \Rightarrow x^2+y^2={9\over 5}+4 =\bbox[red, 2pt]{29\over 5}$$
解答:
$$假設圓半徑r,即\overline{OA}=\overline{OB}=\overline{OP} \Rightarrow \cases{S_1=r^2\pi\cdot {\pi-2\theta\over 2\pi}\\ S_2={1\over 2}\cdot 2r\cdot r\sin(\pi-2\theta)} \\ \Rightarrow \lim_{\theta \to \pi/2}{S_1\over S_2} =\lim_{\theta \to \pi/2} {\pi -2\theta\over 2 \sin(\pi-2\theta)} ={1\over 2}\lim_{\theta \to \pi/2} {{d\over d\theta}(\pi-2\theta)\over {d\over d\theta} \sin(\pi-2\theta)} \\= {1\over 2}\lim_{\theta \to \pi/2}{-2\over -2\cos (\pi-2\theta)}=\bbox[red,2pt]{1\over 2}$$
解答:$$矩陣A對角線元素均為0,右上角均為1,左下角均為-1\\ 因此\cases{EX=0\\ EX^2=(m^2-m)/m^2} \Rightarrow 標準差=\sqrt{m^2-m\over m^2} ={2\sqrt 2\over 3} \Rightarrow {m^2-m\over m^2}={8\over 9} \\ \Rightarrow 1-{1\over m}={8\over 9} \Rightarrow m=\bbox[red, 2pt]9$$
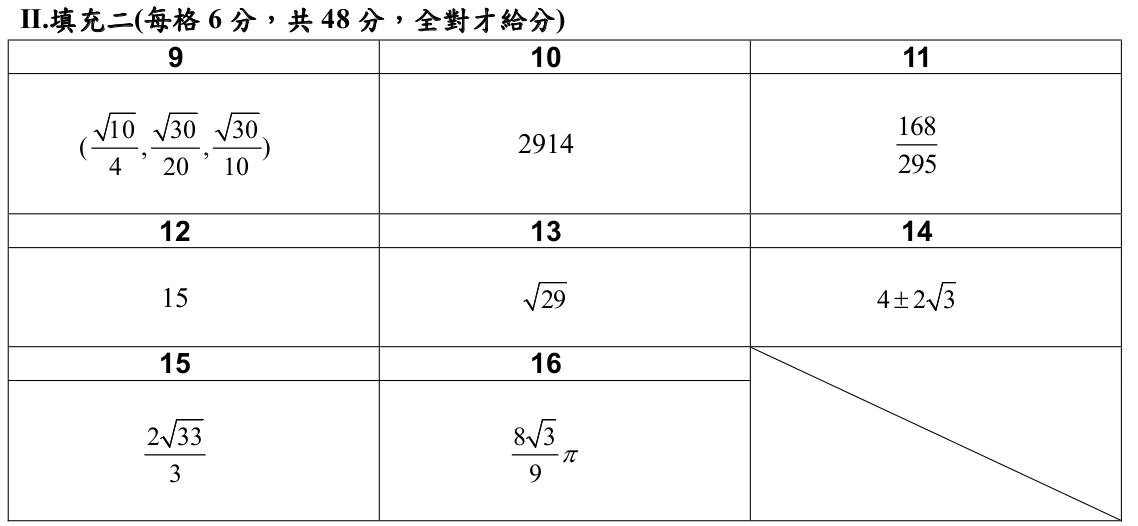
解答:$$令g(x)=f(x)-100x+(x+1) \Rightarrow \cases{g(1)=f(1)-98=0\\ g(2) =f(2)-197=0\\ g(3)=f(3)-296=0} \Rightarrow 1,2,3為g(x)=0的三根\\ \Rightarrow g(x)=(x-1)(x-2)(x-3)(x-\alpha) \Rightarrow \cases{g(8)=f(8)-791=210(8-\alpha)\\ g(-4)=f(-4)+397=-210(-4-\alpha)} \\ \Rightarrow g(8)+g(-4)=f(8)+f(-4)-394=2520 \Rightarrow f(8)+f(-4)=\bbox[red, 2pt]{2914}$$
解答:$$\angle PAB= \angle PBC= \angle PCA \Rightarrow P\text{ 叫正布洛卡點(Brocard point)} \Rightarrow \cot \theta=\cot A+\cot B+\cot C\\ \cases{\cos A=(13^2+15^2-14^2)/2\cdot 13\cdot 15= 33/65\\ \cos B=(13^2+14^2-15^2)/2\cdot 13\cdot 14=5/13 \\ \cos C=(14^2+15^2-13^2)/ 2\cdot 14\cdot 15=3/5} \Rightarrow \cases{\cot A=33/56\\ \cot B=5/12\\ \cot C=3/4} \\\Rightarrow \cot \theta={33\over 65}+ {5\over 13}+{3\over 5} ={295\over 168} \Rightarrow \tan \theta=\bbox[red, 2pt]{168\over 295}\\ \href{https://twsf.ntsec.gov.tw/activity/race-2/2020/pdf/TISF2020-010038.pdf}{公式來源}$$
解答:$$f(x)在x=b的一次近似為2x-5 \Rightarrow 切點(b,f(b))=(b,2b-5)=(b,b) \Rightarrow b=5\\ 又a,b,c成等差\Rightarrow a+c=2b \Rightarrow a+b+c=3b=\bbox[red, 2pt]{15}$$
解答:$$\sqrt{(x-4)^2+ (y-1)^2+(x+y-2)^2}+ \sqrt{(x-4)^2+ (y-2)^2+(x+y)^2} \\=\overline{PA}+ \overline{PB},其中\cases{P(x,y,x+y) \in 平面E:x+y=z\\ A(4,1,2)\\ B(4,2,0)}\\ 過B且方向向量為(1,1,-1)的直線L:x-4=y-2={z\over -1} \Rightarrow B'=E\cap L=(2,0,2)\\ \Rightarrow B'=(B+B'')\div 2 \Rightarrow B''(0,-2,4) \Rightarrow \overline{PA}+ \overline{PB}的最小值=\overline{AB''}= \bbox[red,2pt]{29}$$
解答:$$$$
解答:$$令\overline{BC}中點O為原點,應此取\cases{O(0,0,0)\\ B(-3,0,0)\\ C(3,0,0)\\ D(0,\sqrt 7,0)},再由\cos \theta ={\sqrt 7\over 6} \Rightarrow \tan \theta ={\sqrt {29}\over \sqrt 7} \\\Rightarrow 平面E=\triangle ABC:z=\sqrt{29\over 7}y \Rightarrow 令A(a,b,\sqrt{29\over 27}b) \Rightarrow \cases{\overline{AB}^2 =(a+3)^2+b^2 +{29\over 7}b^2=32\\ \overline{AC}^2=(a-3)^2+ b^2 +{29\over 7}b^2 = 20}\\ \Rightarrow (a+3)^2-(a-3)^2=12 \Rightarrow a=1 \Rightarrow b^2 +{29\over 7}b^2=16 \Rightarrow b= {2\over 3}\sqrt 7 \Rightarrow A(1, {2\over 3}\sqrt 7, {2\over 3} \sqrt{29}) \\ \Rightarrow \overline{AD}^2=1+{7\over 9}+ {4\over 9}\times 29 ={132\over 9} \Rightarrow \overline{AD}=\bbox[red, 2pt]{ {2\over 3}\sqrt{33}}$$
解答:$$假設 P(\alpha, \sqrt{a\alpha}) \Rightarrow \overline{PO}=2 \Rightarrow \alpha^2+a\alpha=4 \Rightarrow \alpha^2+a\alpha-4=0 \\ 旋轉體積=\int_0^\alpha ax\pi \,dx ={1\over 2}a\alpha^2\pi\\ 因此令\cases{f(a,\alpha)={1\over 2}a\alpha^2\pi \\ g(a,\alpha)= \alpha^2+a\alpha-4} ,利用\text{Lagrange 算子求極值}\\ \cases{f_a =\lambda g_a\\ f_\alpha= \lambda g_\alpha}\Rightarrow \cases{{1\over 2}\alpha^2\pi =\lambda \alpha \cdots(1)\\ a\alpha \pi =\lambda(2\alpha+a) \cdots(2)},由(1)得\lambda={1 \over 2}\alpha \pi 代入(2) \Rightarrow a=2\alpha \\ \Rightarrow g(2\alpha,\alpha)=0 \Rightarrow \alpha ={2\over\sqrt 3} \Rightarrow a={4\over \sqrt 3} \Rightarrow f(4/\sqrt 3,2/\sqrt 3)= \bbox[red,2pt]{{8\sqrt 3\over 9}\pi}$$
7. 箱子內有編號 1.2.3.4.5.6 的球各一顆,每一顆球被抽中的機率皆相同。今從中抽取一球後,將編號與該抽中球編號的因數、倍數相同的球移出(例:抽中 3 號,則移出 1.3.6 號球),然後再抽取箱中的球,並重複上述動作,直到球被抽完為止,則最後一次抽取還有兩顆球的機率為 ____
(化為最簡分數)。
解答:$$\cases{抽到1:移出全部,沒剩下\\ 抽到2:移出1,2,4,6,剩下3,5\\ 抽到3:移出1,3,6,剩下2,4,5\to 抽到5,剩下2,4\\ 抽到4:移出1,2,4,剩下3,5,6 \to 抽到5,剩下3,6\\ 抽到5:移出1,5,剩下2,3, 4,6\to 抽到3或6,剩下2,4\\ 抽到6:移出1,2,3,6,剩下4,5 }\\ 第1次抽到2或6會剩下兩球,機率為{1\over 3}\\ 第1次抽到3或4,第2次抽到5會剩下兩張牌,機率為{1\over 9}\\ 第1次抽到5,第2次抽到3或6會剩下兩張牌,機率為{1\over 12}$$
解答:$$f(x)={\sin x+2\over 2 \cos x+3} \Rightarrow f'(x)={4 \sin x+3\cos x+2\over (2\cos x+3)^2}=0 \Rightarrow 4 \sin x+3\cos x+2=0 \\\Rightarrow 4\cdot {2y\over y^2+1}+3\cdot {1-y^2\over y^2+1}+2=0,其中y=\tan{x\over 2} \Rightarrow \cases{\sin x=2y/(y^2+1)\\ \cos x =(1-y^2)/(y^2+1)} \\ \Rightarrow y^2-8y-5=0 \Rightarrow \cases{y=4+\sqrt{21} \Rightarrow f(x)=(6+\sqrt{21})/5\\ y=4-\sqrt{21} \Rightarrow f(x)=(6-\sqrt{21})/5} \\ \Rightarrow f(x)的範圍為\bbox[red, 2pt]{\left[{6-\sqrt{21}\over 5}, {6+\sqrt{21}\over 5}\right]}$$Ⅱ.填充二(每格 6 分,共 48 分,全對才給分)
解答:$$\cases{A(1,0,0)\\ B(1/4,\sqrt 3/4,\sqrt 3/2)} \Rightarrow P=\overline{AB}中點= (5/8,\sqrt 3/8,\sqrt 3/4) \Rightarrow |\overrightarrow{OP}|= {\sqrt{10} \over 4} \\ \Rightarrow \vec n={\overrightarrow{OP} \over |\overrightarrow{OP}|} =({5\over 2\sqrt{10}} ,{\sqrt 3\over 2\sqrt{10}},{\sqrt 3\over \sqrt{10}}) =({\sqrt{10} \over 4}, {\sqrt{30} \over 20},{\sqrt{30} \over 10}) \Rightarrow C= \bbox[red, 2pt]{({\sqrt{10} \over 4}, {\sqrt{30} \over 20},{\sqrt{30} \over 10})}$$解答:$$令g(x)=f(x)-100x+(x+1) \Rightarrow \cases{g(1)=f(1)-98=0\\ g(2) =f(2)-197=0\\ g(3)=f(3)-296=0} \Rightarrow 1,2,3為g(x)=0的三根\\ \Rightarrow g(x)=(x-1)(x-2)(x-3)(x-\alpha) \Rightarrow \cases{g(8)=f(8)-791=210(8-\alpha)\\ g(-4)=f(-4)+397=-210(-4-\alpha)} \\ \Rightarrow g(8)+g(-4)=f(8)+f(-4)-394=2520 \Rightarrow f(8)+f(-4)=\bbox[red, 2pt]{2914}$$
解答:$$\angle PAB= \angle PBC= \angle PCA \Rightarrow P\text{ 叫正布洛卡點(Brocard point)} \Rightarrow \cot \theta=\cot A+\cot B+\cot C\\ \cases{\cos A=(13^2+15^2-14^2)/2\cdot 13\cdot 15= 33/65\\ \cos B=(13^2+14^2-15^2)/2\cdot 13\cdot 14=5/13 \\ \cos C=(14^2+15^2-13^2)/ 2\cdot 14\cdot 15=3/5} \Rightarrow \cases{\cot A=33/56\\ \cot B=5/12\\ \cot C=3/4} \\\Rightarrow \cot \theta={33\over 65}+ {5\over 13}+{3\over 5} ={295\over 168} \Rightarrow \tan \theta=\bbox[red, 2pt]{168\over 295}\\ \href{https://twsf.ntsec.gov.tw/activity/race-2/2020/pdf/TISF2020-010038.pdf}{公式來源}$$
解答:$$f(x)在x=b的一次近似為2x-5 \Rightarrow 切點(b,f(b))=(b,2b-5)=(b,b) \Rightarrow b=5\\ 又a,b,c成等差\Rightarrow a+c=2b \Rightarrow a+b+c=3b=\bbox[red, 2pt]{15}$$
解答:$$\sqrt{(x-4)^2+ (y-1)^2+(x+y-2)^2}+ \sqrt{(x-4)^2+ (y-2)^2+(x+y)^2} \\=\overline{PA}+ \overline{PB},其中\cases{P(x,y,x+y) \in 平面E:x+y=z\\ A(4,1,2)\\ B(4,2,0)}\\ 過B且方向向量為(1,1,-1)的直線L:x-4=y-2={z\over -1} \Rightarrow B'=E\cap L=(2,0,2)\\ \Rightarrow B'=(B+B'')\div 2 \Rightarrow B''(0,-2,4) \Rightarrow \overline{PA}+ \overline{PB}的最小值=\overline{AB''}= \bbox[red,2pt]{29}$$
解答:$$$$
解答:$$令\overline{BC}中點O為原點,應此取\cases{O(0,0,0)\\ B(-3,0,0)\\ C(3,0,0)\\ D(0,\sqrt 7,0)},再由\cos \theta ={\sqrt 7\over 6} \Rightarrow \tan \theta ={\sqrt {29}\over \sqrt 7} \\\Rightarrow 平面E=\triangle ABC:z=\sqrt{29\over 7}y \Rightarrow 令A(a,b,\sqrt{29\over 27}b) \Rightarrow \cases{\overline{AB}^2 =(a+3)^2+b^2 +{29\over 7}b^2=32\\ \overline{AC}^2=(a-3)^2+ b^2 +{29\over 7}b^2 = 20}\\ \Rightarrow (a+3)^2-(a-3)^2=12 \Rightarrow a=1 \Rightarrow b^2 +{29\over 7}b^2=16 \Rightarrow b= {2\over 3}\sqrt 7 \Rightarrow A(1, {2\over 3}\sqrt 7, {2\over 3} \sqrt{29}) \\ \Rightarrow \overline{AD}^2=1+{7\over 9}+ {4\over 9}\times 29 ={132\over 9} \Rightarrow \overline{AD}=\bbox[red, 2pt]{ {2\over 3}\sqrt{33}}$$
解答:$$假設 P(\alpha, \sqrt{a\alpha}) \Rightarrow \overline{PO}=2 \Rightarrow \alpha^2+a\alpha=4 \Rightarrow \alpha^2+a\alpha-4=0 \\ 旋轉體積=\int_0^\alpha ax\pi \,dx ={1\over 2}a\alpha^2\pi\\ 因此令\cases{f(a,\alpha)={1\over 2}a\alpha^2\pi \\ g(a,\alpha)= \alpha^2+a\alpha-4} ,利用\text{Lagrange 算子求極值}\\ \cases{f_a =\lambda g_a\\ f_\alpha= \lambda g_\alpha}\Rightarrow \cases{{1\over 2}\alpha^2\pi =\lambda \alpha \cdots(1)\\ a\alpha \pi =\lambda(2\alpha+a) \cdots(2)},由(1)得\lambda={1 \over 2}\alpha \pi 代入(2) \Rightarrow a=2\alpha \\ \Rightarrow g(2\alpha,\alpha)=0 \Rightarrow \alpha ={2\over\sqrt 3} \Rightarrow a={4\over \sqrt 3} \Rightarrow f(4/\sqrt 3,2/\sqrt 3)= \bbox[red,2pt]{{8\sqrt 3\over 9}\pi}$$












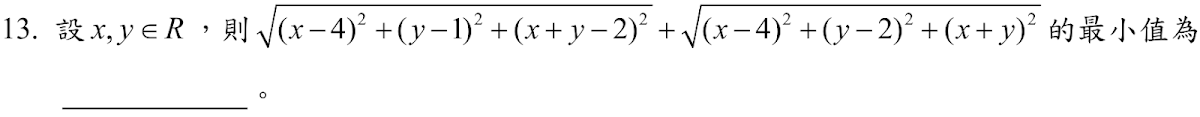
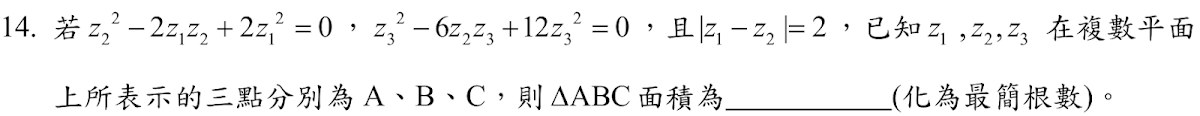



沒有留言:
張貼留言