國立臺灣師範大學附屬高級中學113學年度第2次專任教師甄選
一、 選填題:(每題5分,共90分。填在答案卡上,分數或根式須以最簡形式回答,否則不予計分)
解答:$$假設1號同學寫出的數字為a,則此數列為\langle a_n\rangle,並令數列b_n=a_n-a_{n-1},n=2,3,\dots \\ 則\langle b_n\rangle=\overbrace{2,3,-1}^{循環},2,3,-1 ,\dots \Rightarrow b_n=b_n+3\\因此\sum_{n=1}^{25} a_n =a_1+(a_1+b_1) +(a_1+b_1+b_2) +(a_1+b_1+ b_2+ b_3) +\cdots (a_1+b_1+\cdots+ b_{24}) \\=25a_1+ 24b_1+ 23b_2+ 22b_3+21b_1+20b_2+ 19b_3+ \cdots +b_{3} \\=25a_1+ b_1(24+21+ 18+\cdots+3) +b_2(23+20+\cdots +2) +b_3(22+ 19+\cdots+1) \\=25a+ 2\cdot {27\cdot 8\over 2} +3\cdot {25\cdot 8\over 2}-{23\cdot 8\over 2} = 25a+424\le 2024 \Rightarrow a\le \bbox[red, 2pt]{64}$$解答:$$(1) \Rightarrow f(x)=a(x-1)^2+b \Rightarrow f(2)=a+b=5\\ (2) \Rightarrow y=g(x)=-2(x-1)+b=-2x+b+2 \\ (3) \Rightarrow h(x)=(a(x-1)^2+b) (-2x+b+2) \Rightarrow x^3係數=-2a \Rightarrow |-2a|=6 \\ \Rightarrow a=3\; ( f(x)有最小值\Rightarrow a\gt 0) \Rightarrow b=2 \Rightarrow \cases{f(x)=3(x-1)^2+3\\ g(x)=-2x+4} \\ \Rightarrow h(x)=(3(x-1)^2+3)(-2x+4) \Rightarrow y=p(x)=h(x-1)=(3(x-2)^2+3)(-2x+6)\\ = -6x^3+42x^2-102x+90 \Rightarrow h'(x-1)=-18x^2+84x-102 \Rightarrow h''(h-1)=-36x+84 =0 \\ \Rightarrow x={84\over 36}= \bbox[red, 2pt]{7\over 3}$$
解答:
$$PQRS為平行四邊形 \Rightarrow \cases{\angle SMR= \angle MRQ= \alpha \\ \overline{SR} =\overline{PQ}=6 \\ \angle PMN = \angle MNR=\theta} 又\overline{MN}為摺線 \Rightarrow \cases{ \overline{MR} =\overline{MP} =4\sqrt 3 \\ \angle RMN=\angle PMN =\theta} \\ \triangle MSR: {6\over \sin \alpha} ={4\sqrt 3\over \sin S =\sin Q =\sqrt 5/4} \Rightarrow \sin \alpha= {\sqrt{15} \over 8} \Rightarrow \cos \alpha={7\over 8} \Rightarrow \cos {\alpha\over 2}= {\sqrt{15} \over 4}\\又2\theta+\alpha=180^\circ \Rightarrow \sin \theta= \sin(90^\circ-{\alpha\over 2}) =\cos {\alpha\over 2} ={\sqrt{15} \over 4}\\ \triangle RMN: {\overline{MN} \over \sin \alpha} ={4\sqrt 3\over \sin \theta} \Rightarrow \overline{MN} ={4\sqrt 3\over {\sqrt{15} \over 4}} \cdot {\sqrt{15}\over 8} =\bbox[red, 2pt]{2\sqrt 3}$$
解答:
$$ \begin{array}{c}y& x &數量\\\hline 5&0 & 1\\ 4& (-2)\to2&5 \\ 3& (-4)\to 4 & 9\\ 2,1& (-5) \to 5& 22\\ 0 &(-5)\to 5 & 11\\ -1& (-6)\to 6& 13\\ -2& (-6)\to 6& 13\\ -3& (-4) \to 4& 9\\ -4& (-2)\to 2& 5\\ -5 & 0 & 1\\\hline &\sum & \bbox[red, 2pt]{89} \end{array} $$

解答:$$依題意假設Q(x)=2(x-\alpha)(x-\beta) \Rightarrow f(x)=Q(x^2+8x-17)=2(x^2+8x-17-\alpha) (x^2+8x-17-\beta)\\ f(2)=0 \Rightarrow 2(3-\alpha)(3-\beta)=0 \Rightarrow \alpha=3或\beta=3\\ \text{Case I }\alpha=\beta=3 \Rightarrow f(x)=2(x^2+8x-20)^2=2(x-2)^2(x+10)^2 \\ \text{Case II }\alpha=3,\beta\ne 3 \Rightarrow f(x) =2(x-2)(x+10)(x^2+8x-17-\beta) \Rightarrow x^2+ 8x-17-\beta=0有重根 \\\qquad \Rightarrow 判別式64+4(17+\beta) =0 \Rightarrow \beta=-33 \\令g(x)=Q(2x^2-5x+9) =2(2x^2-5x+9-\alpha) (2x^2-5x+9-\beta)\\ \Rightarrow \cases{\text{Case I }\alpha=\beta=3 \Rightarrow g(1/2) =2(7-3)^2= 32\\ \text{Case II }\alpha=3,\beta=-33 \Rightarrow g(1/2) =2(7-3)(7+33) = 320} \Rightarrow 32+320= \bbox[red, 2pt]{352}$$

解答:$$\cases{A(1,2,3)\\ B(3,4,5)\\ P(x,y,0)} \Rightarrow \overline{PA}^2+ \overline{PB}^2 = (x-1)^2+ (y-2)^2+9 + (x-3)^2+ (y-4)^2+25 \\= 2(x^2+y^2-4x-6y+32)= 2((x-2)^2+ (y-3)^2+ 19)\\ 當\cases{x=2\\ y=3}時,有最小值:2\times 19= \bbox[red, 2pt]{38}$$

解答:$$C^n_2=36 \Rightarrow n=\bbox[red, 2pt]9, \href{https://www.csie.ntu.edu.tw/~yvchen/doc/unlock.pdf}{參考資料}$$
解答:$$n=12代入公式:C^n_0+ C^n_1+ C^n_2 +C^n_3 =C^{12}_0 +C^{12}_1 +C^{12}_2 +C^{12}_3 =1+12+66+ 220 =\bbox[red, 2pt]{299}, \\\href{https://www.youtube.com/watch?v=jImSYbmPPVI}{參考資料}$$
解答:$$(1+x)^{16}=C^{16}_0+C^{16}_1x+ C^{16}_2x^2+ \cdots +C^{16}_{16}x^{16} \\ \Rightarrow f(x)=x(1+x)^{16} =C^{16}_0x+C^{16}_1x^2 + C^{16}_2x^3+ \cdots +C^{16}_{16}x^{17} \\ \Rightarrow f'(x)=(1+x)^{15}(1+17x) = C^{16}_0+2C^{16}_1x + 3C^{16}_2x^2+ \cdots + 17C^{16}_{16}x^{16} \\ \Rightarrow f''(x)= (1+x)^{14}(32+272x) =2C^{16}_1 + 2\cdot 3C^{16}_2x+ 3\cdot 4C^{16}_3x^2 +\cdots + 16\cdot 17C^{16}_{16}x^{15} \\ \Rightarrow f''(1)=2^{14}\times 304 =2C^{16}_1 + 2\cdot 3C^{16}_2+ 3\cdot 4C^{16}_3+\cdots + 16\cdot 17C^{16}_{16} \\ \Rightarrow {1\over 2^{16}}(2C^{16}_1 + 2\cdot 3C^{16}_2+ 3\cdot 4C^{16}_3+\cdots + 16 \cdot 17C^{16}_{16}) ={2^{14}\times 304\over 2^{16}} = \bbox[red, 2pt]{76}$$
解答:$$I=\lim_{n\to \infty}\sum_{k=1}^{2n}{4n^2\over (2n+5k)^3} =\lim_{n\to \infty}\sum_{k=1}^{2n}{4/n\over (2+5k/n)^3} = \int_0^2 {4\over (2+5x)^3} \,dx \\ u=2+5x \Rightarrow du=5\,dx \Rightarrow I=\int_{2}^{12} {4\over 5u^3}\,du =\bbox[red, 2pt]{7\over 72}$$
解答:$$x^7=2^7的7根分別為2,\omega,\omega^2,\dots,\omega^6,其\omega =2e^{2\pi/7}\\ \Rightarrow f(x)=x^7-2^7=(x-2)(x-\omega)(x-\omega^2)\cdots(x-\omega^6) \\ \Rightarrow |f(x)|=|x^7-2^7|=|x-2||x-\omega||x-\omega^2| \cdots |x-\omega^6| \\ \Rightarrow |f(1+i)|=|(1+i)^7-2^7|= \overline{PA}\cdot \overline{PB} \cdot \overline{PC}\cdot\cdots \cdot\overline {PG} \\ 又(1+i)^2=2i \Rightarrow (1+i)^6=-8i \Rightarrow (1+i)^7=8-8i \Rightarrow |f(1+i)|=|8-8i-2^7| \\=|-120-8i|= \sqrt{120^2 +8^2} =\bbox[red,2pt]{ 8\sqrt{226}}$$

解答:$$\cases{L_1方向向量\vec u=(3,6,-5\sqrt 3) \\L_2方向向量\vec v=(-2,1,0)} \Rightarrow \vec n=\vec u\times \vec v=(5\sqrt 3,10\sqrt 3,15) \\ \Rightarrow 法向量為\vec n且通過L_2上的點(0,0,0)的平面E:\sqrt 3x+2\sqrt3 y+3z=0\\ L_1上的點(1,2,\sqrt 3)至E的距離=2\sqrt 2 =d(L_1,L_2) \Rightarrow 稜長a=2\sqrt 2\cdot \sqrt 2=4\\ \Rightarrow 體積={1\over 12}\sqrt 2a^3= \bbox[red, 2pt]{{16\over 3}\sqrt 2}$$

解答:$$X_i=擲出i種點數所需的次數 \Rightarrow X=X_1+X_2+\cdots+X_6且X_i \sim Geo(p_i={7-i\over 6}) \Rightarrow E(X_i)={6\over 7-i}\\ \Rightarrow E(X) =E(X_1+X_2+\cdots+X_6) =E(X_1) +E(X_2)+ \cdots+E(X_6)\\ =1+{6\over 5} +{6\over 4} +{6\over 3} +{6\over 2} +{6\over 1} =\bbox[red, 2pt]{14.7}, \href{https://blog.csdn.net/Rocky6688/article/details/103335048}{參考資料}$$

解答:$$\Gamma_1=\Gamma_2 \Rightarrow {2\over 9}x^3-{8\over 3}x+6k+6 =0 \Rightarrow x^3-12x+27k+27=0 \\ 令f(x)=x^3-12x+27k+27 \Rightarrow f'(x)=0 \Rightarrow 3x^2-12=0 \Rightarrow x=\pm 2\\ f(x)=0有三相異實根\Rightarrow f(2)f(-2) \lt 0 \Rightarrow (27k+11)(27k+43)\lt 0 \Rightarrow -{43\over 27}\lt k\lt -{11\over 27} \\ \Rightarrow k=-1 (\because k是整數) \Rightarrow f(x)=x^3-12x=0 \Rightarrow x=0,\pm 2\sqrt 3\\ \Rightarrow \Gamma_1-\Gamma_2 =g(x)={2\over 9}x^3-{8\over 3}x \Rightarrow g(x)是奇函數 \Rightarrow \int_{-2\sqrt 3}^{2\sqrt 3} |g(x)|\,dx =2\int_{0}^{2\sqrt 3} |g(x)|\,dx \\= 2\left. \left[ {2\over 36}x^4-{4\over 3}x^2 \right] \right|_{2\sqrt 3}^0 = \bbox[red, 2pt]{16}$$
解答:$$取\cases{u=19x+13y\\ v=25x+17y} \Rightarrow \left|{\partial (u,v) \over \partial (x,y)} \right| =\begin{Vmatrix} 19& 13\\ 25& 17\end{Vmatrix} =2 \\ {|u|\over 3}+{|v|\over 4}=1所圍面積= 3\times 4\times 2=24 \Rightarrow {|19x+13y|\over 3}+{|25x+17y|\over 4}=1所圍面積= {24\over 2}= \bbox[red, 2pt]{12}$$
解答:

解答:$$依題意假設Q(x)=2(x-\alpha)(x-\beta) \Rightarrow f(x)=Q(x^2+8x-17)=2(x^2+8x-17-\alpha) (x^2+8x-17-\beta)\\ f(2)=0 \Rightarrow 2(3-\alpha)(3-\beta)=0 \Rightarrow \alpha=3或\beta=3\\ \text{Case I }\alpha=\beta=3 \Rightarrow f(x)=2(x^2+8x-20)^2=2(x-2)^2(x+10)^2 \\ \text{Case II }\alpha=3,\beta\ne 3 \Rightarrow f(x) =2(x-2)(x+10)(x^2+8x-17-\beta) \Rightarrow x^2+ 8x-17-\beta=0有重根 \\\qquad \Rightarrow 判別式64+4(17+\beta) =0 \Rightarrow \beta=-33 \\令g(x)=Q(2x^2-5x+9) =2(2x^2-5x+9-\alpha) (2x^2-5x+9-\beta)\\ \Rightarrow \cases{\text{Case I }\alpha=\beta=3 \Rightarrow g(1/2) =2(7-3)^2= 32\\ \text{Case II }\alpha=3,\beta=-33 \Rightarrow g(1/2) =2(7-3)(7+33) = 320} \Rightarrow 32+320= \bbox[red, 2pt]{352}$$

解答:$$\cases{A(1,2,3)\\ B(3,4,5)\\ P(x,y,0)} \Rightarrow \overline{PA}^2+ \overline{PB}^2 = (x-1)^2+ (y-2)^2+9 + (x-3)^2+ (y-4)^2+25 \\= 2(x^2+y^2-4x-6y+32)= 2((x-2)^2+ (y-3)^2+ 19)\\ 當\cases{x=2\\ y=3}時,有最小值:2\times 19= \bbox[red, 2pt]{38}$$

解答:$$C^n_2=36 \Rightarrow n=\bbox[red, 2pt]9, \href{https://www.csie.ntu.edu.tw/~yvchen/doc/unlock.pdf}{參考資料}$$
解答:$$n=12代入公式:C^n_0+ C^n_1+ C^n_2 +C^n_3 =C^{12}_0 +C^{12}_1 +C^{12}_2 +C^{12}_3 =1+12+66+ 220 =\bbox[red, 2pt]{299}, \\\href{https://www.youtube.com/watch?v=jImSYbmPPVI}{參考資料}$$
解答:$$(1+x)^{16}=C^{16}_0+C^{16}_1x+ C^{16}_2x^2+ \cdots +C^{16}_{16}x^{16} \\ \Rightarrow f(x)=x(1+x)^{16} =C^{16}_0x+C^{16}_1x^2 + C^{16}_2x^3+ \cdots +C^{16}_{16}x^{17} \\ \Rightarrow f'(x)=(1+x)^{15}(1+17x) = C^{16}_0+2C^{16}_1x + 3C^{16}_2x^2+ \cdots + 17C^{16}_{16}x^{16} \\ \Rightarrow f''(x)= (1+x)^{14}(32+272x) =2C^{16}_1 + 2\cdot 3C^{16}_2x+ 3\cdot 4C^{16}_3x^2 +\cdots + 16\cdot 17C^{16}_{16}x^{15} \\ \Rightarrow f''(1)=2^{14}\times 304 =2C^{16}_1 + 2\cdot 3C^{16}_2+ 3\cdot 4C^{16}_3+\cdots + 16\cdot 17C^{16}_{16} \\ \Rightarrow {1\over 2^{16}}(2C^{16}_1 + 2\cdot 3C^{16}_2+ 3\cdot 4C^{16}_3+\cdots + 16 \cdot 17C^{16}_{16}) ={2^{14}\times 304\over 2^{16}} = \bbox[red, 2pt]{76}$$
解答:$$I=\lim_{n\to \infty}\sum_{k=1}^{2n}{4n^2\over (2n+5k)^3} =\lim_{n\to \infty}\sum_{k=1}^{2n}{4/n\over (2+5k/n)^3} = \int_0^2 {4\over (2+5x)^3} \,dx \\ u=2+5x \Rightarrow du=5\,dx \Rightarrow I=\int_{2}^{12} {4\over 5u^3}\,du =\bbox[red, 2pt]{7\over 72}$$
解答:$$x^7=2^7的7根分別為2,\omega,\omega^2,\dots,\omega^6,其\omega =2e^{2\pi/7}\\ \Rightarrow f(x)=x^7-2^7=(x-2)(x-\omega)(x-\omega^2)\cdots(x-\omega^6) \\ \Rightarrow |f(x)|=|x^7-2^7|=|x-2||x-\omega||x-\omega^2| \cdots |x-\omega^6| \\ \Rightarrow |f(1+i)|=|(1+i)^7-2^7|= \overline{PA}\cdot \overline{PB} \cdot \overline{PC}\cdot\cdots \cdot\overline {PG} \\ 又(1+i)^2=2i \Rightarrow (1+i)^6=-8i \Rightarrow (1+i)^7=8-8i \Rightarrow |f(1+i)|=|8-8i-2^7| \\=|-120-8i|= \sqrt{120^2 +8^2} =\bbox[red,2pt]{ 8\sqrt{226}}$$

解答:$$\cases{L_1方向向量\vec u=(3,6,-5\sqrt 3) \\L_2方向向量\vec v=(-2,1,0)} \Rightarrow \vec n=\vec u\times \vec v=(5\sqrt 3,10\sqrt 3,15) \\ \Rightarrow 法向量為\vec n且通過L_2上的點(0,0,0)的平面E:\sqrt 3x+2\sqrt3 y+3z=0\\ L_1上的點(1,2,\sqrt 3)至E的距離=2\sqrt 2 =d(L_1,L_2) \Rightarrow 稜長a=2\sqrt 2\cdot \sqrt 2=4\\ \Rightarrow 體積={1\over 12}\sqrt 2a^3= \bbox[red, 2pt]{{16\over 3}\sqrt 2}$$

解答:$$X_i=擲出i種點數所需的次數 \Rightarrow X=X_1+X_2+\cdots+X_6且X_i \sim Geo(p_i={7-i\over 6}) \Rightarrow E(X_i)={6\over 7-i}\\ \Rightarrow E(X) =E(X_1+X_2+\cdots+X_6) =E(X_1) +E(X_2)+ \cdots+E(X_6)\\ =1+{6\over 5} +{6\over 4} +{6\over 3} +{6\over 2} +{6\over 1} =\bbox[red, 2pt]{14.7}, \href{https://blog.csdn.net/Rocky6688/article/details/103335048}{參考資料}$$

解答:$$\Gamma_1=\Gamma_2 \Rightarrow {2\over 9}x^3-{8\over 3}x+6k+6 =0 \Rightarrow x^3-12x+27k+27=0 \\ 令f(x)=x^3-12x+27k+27 \Rightarrow f'(x)=0 \Rightarrow 3x^2-12=0 \Rightarrow x=\pm 2\\ f(x)=0有三相異實根\Rightarrow f(2)f(-2) \lt 0 \Rightarrow (27k+11)(27k+43)\lt 0 \Rightarrow -{43\over 27}\lt k\lt -{11\over 27} \\ \Rightarrow k=-1 (\because k是整數) \Rightarrow f(x)=x^3-12x=0 \Rightarrow x=0,\pm 2\sqrt 3\\ \Rightarrow \Gamma_1-\Gamma_2 =g(x)={2\over 9}x^3-{8\over 3}x \Rightarrow g(x)是奇函數 \Rightarrow \int_{-2\sqrt 3}^{2\sqrt 3} |g(x)|\,dx =2\int_{0}^{2\sqrt 3} |g(x)|\,dx \\= 2\left. \left[ {2\over 36}x^4-{4\over 3}x^2 \right] \right|_{2\sqrt 3}^0 = \bbox[red, 2pt]{16}$$
解答:$$取\cases{u=19x+13y\\ v=25x+17y} \Rightarrow \left|{\partial (u,v) \over \partial (x,y)} \right| =\begin{Vmatrix} 19& 13\\ 25& 17\end{Vmatrix} =2 \\ {|u|\over 3}+{|v|\over 4}=1所圍面積= 3\times 4\times 2=24 \Rightarrow {|19x+13y|\over 3}+{|25x+17y|\over 4}=1所圍面積= {24\over 2}= \bbox[red, 2pt]{12}$$
解答:
$$\Gamma_1:\overline{BC}=10 \Rightarrow c=5 \Rightarrow b^2=d(B,L)\cdot d(C,L) ={25\over \sqrt 5} \cdot {15\over \sqrt 5} =75 \Rightarrow b=5\sqrt 3 \Rightarrow a=\sqrt{75+25} = 10\\ \Rightarrow \Gamma_1:{(x+1)^2\over 100} +{y^2\over 75}=1 \\ \Gamma_2:c=5 \Rightarrow {(x+1)^2\over k}-{y^2\over 25-k}=1通過D(-6,{9\over 4}) \Rightarrow {25\over k}-{81/16\over 25-k}=1 \Rightarrow 16k^2-881k+10000=0\\ \quad \Rightarrow (16k-625)(k-16) =0 \Rightarrow \cases{k=625/16 \Rightarrow a=25/4 \gt c(5)不合\\ k=16 \Rightarrow a=4} \Rightarrow \Gamma_2:{(x+1)^2\over 16}-{y^2\over 9}=1 \\ 因此 \Gamma_1 \cap \Gamma_2 \Rightarrow (x+1)^2=100\left( 1-{y^2\over 75}\right) =16\left(1+{y^2\over 9} \right) \Rightarrow y^2=27 \Rightarrow |y|=3\sqrt 3 \\ \Rightarrow s_{\triangle ABC}={1\over 2}\cdot \overline{BC}\cdot |y|={1\over 2}\cdot 10\cdot 3\sqrt 3= \bbox[red, 2pt]{15\sqrt 3}\\ 橢圓兩焦點至切線距離的乘積=b^2, \href{https://www.sohu.com/a/575876952_121124316}{參考資料}$$
解答:$$x^2+xy+y^2 =[x,y] \begin{bmatrix}1& 1/2\\ 1/2 & 1 \end{bmatrix} \begin{bmatrix}x\\ y \end{bmatrix} =[x,y] \left[ \begin{matrix}\frac{-\sqrt{2}}{2} & \frac{\sqrt{2}}{2} \\\frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2}\end{matrix} \right] \left[ \begin{matrix}\frac{1}{2} & 0 \\0 & \frac{3}{2} \end{matrix} \right] \left[ \begin{matrix}\frac{-\sqrt{2}}{2} & \frac{\sqrt{2}}{2} \\\frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2}\end{matrix} \right]^T\begin{bmatrix}x\\ y \end{bmatrix} \\ 取[x',y'] =[x,y] \left[ \begin{matrix}\frac{-\sqrt{2}}{2} & \frac{\sqrt{2}}{2} \\\frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2}\end{matrix} \right] = \left[{\sqrt 2\over 2}(-x+y), {\sqrt 2\over 2}(x+y)\right] \Rightarrow \cases{x={y'-x'\over \sqrt 2} \\y={x'+y'\over \sqrt 2}} \\ \Rightarrow \cases{x^2+xy +y^2 ={x'^2\over 2} +{y'^2\over 2/3}=1 \cdots(1)\\ x^2-3xy-2y^2= x'^2-3x'y'-2y'^2 \cdots(2)} ,由(1) \Rightarrow \cases{x'=\sqrt 2\cos \theta\\ y'=\sqrt{2\over 3} \sin \theta} 代入(2) \\ \Rightarrow 2\cos^2\theta-2\sqrt 3\sin \theta\cos \theta-{4\over 3}\sin^2\theta ={5\over 3} \cos 2\theta-\sqrt 3\sin 2\theta +{1\over 3} \\ \Rightarrow 最大值=\sqrt{{25\over 9}+3}+{1\over 3} = \bbox[red, 2pt]{1+2\sqrt{13} \over 3}$$
====================== END ===================
解答:$$x^2+xy+y^2 =[x,y] \begin{bmatrix}1& 1/2\\ 1/2 & 1 \end{bmatrix} \begin{bmatrix}x\\ y \end{bmatrix} =[x,y] \left[ \begin{matrix}\frac{-\sqrt{2}}{2} & \frac{\sqrt{2}}{2} \\\frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2}\end{matrix} \right] \left[ \begin{matrix}\frac{1}{2} & 0 \\0 & \frac{3}{2} \end{matrix} \right] \left[ \begin{matrix}\frac{-\sqrt{2}}{2} & \frac{\sqrt{2}}{2} \\\frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2}\end{matrix} \right]^T\begin{bmatrix}x\\ y \end{bmatrix} \\ 取[x',y'] =[x,y] \left[ \begin{matrix}\frac{-\sqrt{2}}{2} & \frac{\sqrt{2}}{2} \\\frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2}\end{matrix} \right] = \left[{\sqrt 2\over 2}(-x+y), {\sqrt 2\over 2}(x+y)\right] \Rightarrow \cases{x={y'-x'\over \sqrt 2} \\y={x'+y'\over \sqrt 2}} \\ \Rightarrow \cases{x^2+xy +y^2 ={x'^2\over 2} +{y'^2\over 2/3}=1 \cdots(1)\\ x^2-3xy-2y^2= x'^2-3x'y'-2y'^2 \cdots(2)} ,由(1) \Rightarrow \cases{x'=\sqrt 2\cos \theta\\ y'=\sqrt{2\over 3} \sin \theta} 代入(2) \\ \Rightarrow 2\cos^2\theta-2\sqrt 3\sin \theta\cos \theta-{4\over 3}\sin^2\theta ={5\over 3} \cos 2\theta-\sqrt 3\sin 2\theta +{1\over 3} \\ \Rightarrow 最大值=\sqrt{{25\over 9}+3}+{1\over 3} = \bbox[red, 2pt]{1+2\sqrt{13} \over 3}$$
解答:$$請參閱下方學校提供的解答$$
====================== END ===================
解題僅供參考,教甄歷年試題及詳解










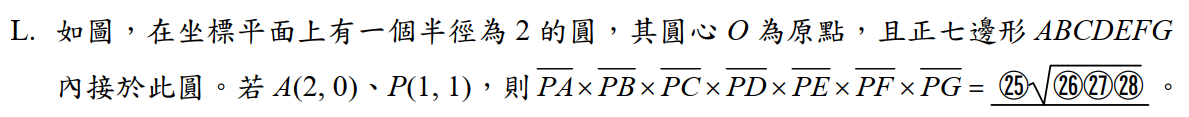








選填D y=0時, x=-5~5吧?從圖也可以看出來
回覆刪除圖畫錯了,已修訂,謝謝指正!
刪除