新竹市立香山高級中學 1 1 4 學年度教師甄選
一、單選題(每題 5 分,共計 50 分)
解答:$$\lim_{n\to \infty} \left({1\over n+1}+{1\over n+2}+ {1\over n+3}+ \cdots +{1\over n+(n-1) }+{1\over n+n } \right) \\= \lim_{n\to \infty} \sum_{k=1}^n {1\over n+k} = \lim_{n\to \infty} \sum_{k=1}^n {1/n\over 1+k/n} =\int_0^1 {1\over 1+x}\,dx =\left.\left[ \ln(1+x) \right] \right|_0^1 =\ln 2,故選\bbox[red, 2pt]{(A)}$$
解答:$$\lim_{x\to 0}{f(3x)-f(\sin x) \over x} =\lim_{x\to 0}{(f(3x)-f(\sin x)') \over (x)'} =\lim_{x\to 0}{3f'(3x)-\cos xf'(\sin x) \over 1} \\=3\cdot 3-1\cdot 3=6,故選\bbox[red, 2pt]{(D)}$$
解答:$$f(x)=(x+1)^n =\sum_{k=0}^n C^n_k x^k \Rightarrow f(1)=2^n =\sum_{k=0}^n C^n_k \Rightarrow C^n_1+ C^n_2 +\cdots +C^n_n=2^n-1 \\ \Rightarrow 2000\lt 2^n-1\lt 3000 \Rightarrow 2001\lt 2^n \lt 3001 \Rightarrow n=11,故選\bbox[red, 2pt]{(B)}$$
解答:$$\tan 1^\circ \cdot \tan 2^\circ \cdot \tan 3^\circ \cdots \tan 89^\circ \\=[\tan 1^\circ \cdot \tan 2^\circ \cdots \tan 44^\circ] \cdot \tan 45^\circ \cdot [\tan(90^\circ-44^\circ)\cdot \tan(90^\circ-43^\circ) \cdots \tan (90^\circ-1^\circ)] \\=[\tan 1^\circ \cdot \tan 2^\circ \cdots \tan 44^\circ] \cdot \tan 45^\circ \cdot [\cot 44^\circ\cdot \cot 43^\circ \cdots \cot 1^\circ] \\= [\tan 1^\circ \cot 1^\circ] [\tan 2^\circ \cot 2^\circ] \cdots[\tan 44^\circ \cot 44^\circ] \tan 45^\circ 1\cdot 1\cdots 1=1 \\ \Rightarrow \log(\tan 1^\circ) +\log(\tan 2^\circ)+ \cdots+\log(\tan 89^\circ) =\log (\tan 1^\circ \cdot \tan 2^\circ \cdots \tan 89^\circ) \\=\log 1=0,故選\bbox[red, 2pt]{(C)}$$

解答:$$\overline{AB} =\overline{AC}=2 \Rightarrow \cos B={2^2+\overline{BC}^2-2^2\over 2\cdot 2\cdot \overline{BC}} ={\overline{BC} \over 4} \\ \triangle ABP_k中\Rightarrow \cos B={4+\overline{BP_k}^2-\overline{AP_k}^2 \over 4\overline{BP_k}} ={\overline{BC}\over 4} \Rightarrow \overline{AP_k}^2+ \overline{BP_k} \cdot \overline{BC}-\overline{BP_k}^2=4 \\ \Rightarrow \overline{AP_k}^2+ \overline{BP_k} ( \overline{BC}-\overline{BP_k})=4 \Rightarrow a_k=\overline{AP_k}^2+ \overline{BP_k} \cdot \overline{P_kC}=4 \\ \Rightarrow \sum_{k=1}^{100} a_k= 100\cdot 4=400,故選\bbox[red, 2pt]{(D)}$$
解答:$${\sqrt{1+\tan x}-\sqrt{1+\sin x}\over x^3} ={\tan x-\sin x\over x^3(\sqrt{1+\tan x}+\sqrt{1+\sin x})} ={\tan x-\sin x\over x^3}\cdot {1\over \sqrt{1+\tan x}+\sqrt{1+\sin x}} \\ 其中\lim_{x\to 0} {1 \over \sqrt{1+\tan x}+\sqrt{1+\sin x}}={1\over 2} 及\lim_{x\to 0}{\tan x-\sin x\over x^3} = \lim_{x\to 0}{\sec^2 x-\cos x\over 3x^2}\\ = \lim_{x\to 0}{2\sec^2 x\tan x+\sin x\over 6x} = \lim_{x\to 0}{4\sec^2 x \tan^2 x+ 2\sec^4 x+ \cos x\over 6} ={0+2+1\over 6}={1\over 2} \\ \Rightarrow \lim_{x\to 0} {\sqrt{1+\tan x}-\sqrt{1+\sin x}\over x^3} ={1\over 2} \cdot {1\over 2}={1\over 4},故選\bbox[red, 2pt]{(B)}$$
解答:$$\cos A=\cos 120^\circ =-{1\over 2} ={4^2+2^2-\overline{BC}^2\over 2\cdot 2\cdot 4} \Rightarrow \overline{BC}=2\sqrt 7\\ \overline{AD}為\angle A的角平分線\Rightarrow {\overline{BD}\over \overline{CD} }={\overline{AB}\over \overline{AC}} ={4\over 2} \Rightarrow \overline{CD} ={1\over 3}\overline{BC} ={2\over 3}\sqrt 7 \\ \Rightarrow \cos \angle CAD=\cos 60^\circ={1\over 2} ={2^2+\overline{AD}^2-(2\sqrt 7/3)^2 \over 2\cdot 2\cdot \overline{AD}} \Rightarrow \overline{AD}={4\over 3},故選\bbox[red, 2pt]{(C)}$$
二、多選題(每題 7 分,共計 35 分;每題有 5 個選項,其中至少有一個是正確的選項)
解答:$$,故選\bbox[red, 2pt]{()}$$
解答:$$\cases{a,c\in \mathbb N\\ c-a=19} \Rightarrow c=19+a \Rightarrow c\ge 20又c^3為一完全平方數\Rightarrow c是完全平方數\\ 又a^5=b^4 \Rightarrow a是一四次方數,因此c=10^2=100 \Rightarrow a=100-19=81=3^4\\ \Rightarrow \cases{d^2=c^3=10^6\\ b^4=a^5=3^{20}} \Rightarrow \cases{d=1000\\ b=3^5=243} \\ (A)\times: 99不是完全平方數\\ (B)\bigcirc: b-a=243-81=162 \\(C)\times: b-c=243-100=143\ne 141\\ (D)\bigcirc: d-a=1000-81=919 \\(E) \bigcirc: a+b-c=81+243-100=224\\,故選\bbox[red, 2pt]{(BDE)}$$
解答:$$ (A)\bigcirc: \sqrt 4\lt \sqrt 6\lt \sqrt 9 \Rightarrow \cases{a=2\\ b=\sqrt 6-2} \\(B)\times: b=3-\sqrt 6\lt 0\\ (C)\bigcirc: {5\over b} ={5\over \sqrt 6-2} ={5\over 2}(\sqrt 6+2) =5+{5\over 2}\sqrt 6 =5+\sqrt{37.5} 整數部分為5+6=11 \\(D)\bigcirc: 2n+11 =2025 \Rightarrow n=1007\\ (E)\times: n=1007\ne 1008\\,故選\bbox[red, 2pt]{(ACD)}$$
三、填充題(每題 5 分,共計 15 分) 請於答案卷 作答
解答:$$\cases{m-184=s^2\\ m+24=t^2},s,t\in \mathbb N \Rightarrow m=s^2+184=t^2-24 \Rightarrow t^2-s^2= (t+s)(t-s)=208 \\ 假設\cases{t+s= u\\ t-s=v} \Rightarrow t=(u+v)/2為自然數 \Rightarrow u+v為偶數,且越大越好\\ 208=1\times208 (u+v為奇數),2\times104 \Rightarrow \cases{t+s=104\\ t-s=2} \Rightarrow t=53 \Rightarrow m=53^2-24= \bbox[red, 2pt]{2785}$$解答:$$A=36^\circ \Rightarrow \cases{5A=180^\circ\\ 3A=180^\circ-2A} \Rightarrow \cos(3A)= \cos(180^\circ-2A) =-\cos(2A) \\ \Rightarrow 4\cos^3 A-3\cos A=1-2\cos^2 A \Rightarrow 4\cos^3A+2\cos^2 A-3\cos A-1=0 \\ \Rightarrow (\cos A+1)(4\cos^2A-2\cos A-1) =0 \Rightarrow \cos A= \cos 36^\circ ={1+\sqrt 5\over 4} \\ 假設\cases{\overline{AB}= \overline{AC}=a\\ \overline{BC}=b} \Rightarrow \cos C= \cos{180^\circ-108^\circ \over 2} =\cos 36^\circ ={a^2+b^2-a^2 \over 2ab} ={b\over 2a} \\ \Rightarrow {\overline{BC} \over \overline{AB}} ={b\over a}=2\cos 36^\circ =2\cdot {1+\sqrt 5\over 4}= \bbox[red, 2pt]{1+\sqrt 5\over 2}$$
解題僅供參考,其他教甄試題及詳解







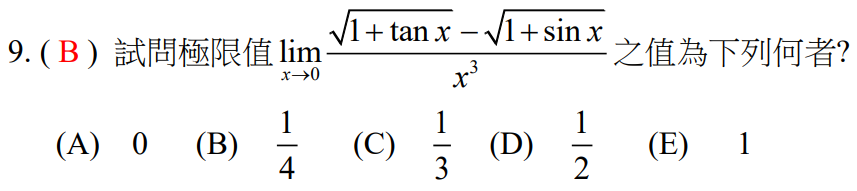








沒有留言:
張貼留言