114 學年度高級中等以上學校運動成績優良學生升學輔導甄試學科考試 數學科試題
說明:單選題共 40 題,請在「答案卡」上劃記。每題 2.5 分,共 100 分。
解答:$$2025^2-2\times 2025\times 2023+2023^2 =(2025-2023)^2 =2^2=4,故選\bbox[red, 2pt]{(E)}$$解答:$$(\sqrt 3-1)^2= 4-2\sqrt 3 \Rightarrow \sqrt{4-2\sqrt 3}=\sqrt 3-1,故選\bbox[red, 2pt]{(A)}$$
解答:$$(A)\times: 2^4+2^3=2^3(2+1)=8\times 3=24 \ne 2^7=128\\ (B) \times 2^4-2^3=2^3(2-1)=2^3=8\ne 2\\ (C)\times: 2^4\times 2^3 =2^{4+3}=2^7 \ne 2^{12}\\ (D)\bigcirc:(2^3)^4= 2^{3\times 4} =2^{12} \\(E)\times: {2^4\over 2^3} =2^{4-3}=2 \ne{1\over 2}\\,故選\bbox[red, 2pt]{(D)}$$
解答:$$\log 2025=\log (2.025\times 10^3) =\log 2.025+\log 10^3= \log 2.025+3=x+3,故選\bbox[red, 2pt]{(C)}$$
解答:$$a_n={2\over n(n+1)} \Rightarrow a_5 ={2\over 5\cdot 6} ={1\over 15},故選\bbox[red, 2pt]{(B)}$$
解答:$$a_4^2=a_3\times a_5=9\times 4=36 \Rightarrow a_4=\sqrt{36}=6,故選\bbox[red, 2pt]{(C)}$$
解答:$$(A)\times: 圖形為凹向上\Rightarrow a\gt 0\\ (B)\bigcirc: 圖形與x軸無交點\Rightarrow f(x)=0無實數解\Rightarrow D\lt 0 \\(C)\times:理由同(B) \\(D)\times:理由同(B) \\(E)\times: 圖形皆在x軸之上\Rightarrow f(x)\gt 0\\,故選\bbox[red, 2pt]{(B)}$$
解答:$$f(x)=(x^2-x+3)(x+4)+ (2x-3),故選\bbox[red, 2pt]{(D)}$$
解答:$$f(x)=x^3-3x^2+2x+1 = (x-1)^3+p(x-1)+k \Rightarrow f(1)=1-3+2+1=1=k \Rightarrow k=1\\ f'(x)=3(x-1)^2+p \Rightarrow f''(x)=6(x-1) =0 \Rightarrow x=1 \Rightarrow 對稱中心(1,f(1))=(1,1),故選\bbox[red, 2pt]{(A)}$$
解答:$$f(x) =(x-1)^3+2(x-1)+3 \Rightarrow f'(x)=3(x-1)^2+2 \Rightarrow f'(1)=2,故選\bbox[red, 2pt]{(E)}$$
解答:$$y=0 \Rightarrow 2x-0+6=0 \Rightarrow x=-3,故選\bbox[red, 2pt]{(A)}$$
解答:$$L斜率={-1-1\over 4-2}={-2\over 2}=-1 \Rightarrow 垂直L的直線斜率=1,故選\bbox[red, 2pt]{(D)}$$
解答:$${|-4+3-9|\over \sqrt{4^2+3^2}} ={10\over 5}=2,故選\bbox[red, 2pt]{(C)}$$
解答:$$1-k=4^2 =16\Rightarrow k=-15,故選\bbox[red, 2pt]{(B)}$$
解答:$$本題\bbox[cyan, 2pt]{送分}$$
解答:$$x,y無相關,故選\bbox[red, 2pt]{(C)}$$
解答:$$\sigma({X\over 100}) ={1\over 100}\sigma(X),故選\bbox[red, 2pt]{(A)}$$
解答:$$n(A\cap B)=n(A)+n(B)-n(A\cup B)=8+9-11=6,故選\bbox[red, 2pt]{(B)}$$
解答:$$4!=24,故選\bbox[red, 2pt]{(E)}$$
解答:$$C^6_2=15,故選\bbox[red, 2pt]{(D)}$$
解答:$${3\over 5+4+3}={3\over 12} ={1\over 4},故選\bbox[red, 2pt]{(B)}$$
解答:$$A與B為獨立事件\Rightarrow P(A\cap B)=P(A)P(B) \Rightarrow {P(A\cap B)\over P(A)} =P(B)={1\over 3},故選\bbox[red, 2pt]{(C)}$$
解答:$${1\over 6}(60+60+6+6+6+6) ={1\over 6}\times 144=24,故選\bbox[red, 2pt]{(E)}$$
解答:$$\sin 21^\circ =\cos(90^\circ-21^\circ) =\cos 69^\circ \Rightarrow \sin^2 21^\circ+\sin^2 69^\circ=\cos^2 69^\circ+ \sin^269^\circ =1,故選\bbox[red, 2pt]{(D)}$$
解答:$$\cos 240^\circ =\cos(180^\circ+60^\circ) =-\cos 60^\circ =-{1\over 2},故選\bbox[red, 2pt]{(A)}$$
解答:$$正弦定理:{\overline{BC} \over \sin\angle BAC} =2R \Rightarrow {2\sqrt 2\over 1/\sqrt 2}= 4=2R \Rightarrow R=2,故選\bbox[red, 2pt]{(D)}$$
解答:$${180^\circ\over \pi} ={300^\circ \over x} \Rightarrow x={300\over 180}\pi ={5\over 3}\pi,故選\bbox[red, 2pt]{(E)}$$
解答:$$-1\le \sin (2x)\le 1 \Rightarrow -3\le 3\sin(2x)\le 3 \Rightarrow -4\le 3\sin(2x)-1 \le 2 \Rightarrow 最大值為2,故選\bbox[red, 2pt]{(B)}$$
解答:$$3^x=12 \Rightarrow \log_3 3^x=\log_3 12 \Rightarrow x=\log_3 12,故選\bbox[red, 2pt]{(C)}$$
解答:$$f(x)與g(x)互為反函數\Rightarrow 兩圖形交於直線y=x \Rightarrow 交點為(x,x) =(x,2^x) \Rightarrow x=2^x\\ \Rightarrow 無交點,故選\bbox[red, 2pt]{(A)}$$
解答:$$(\overrightarrow{BA}+ \overrightarrow{BC})平行於\overrightarrow{BE},故選\bbox[red, 2pt]{(B)}$$
解答:$$\cases{\vec a=(3,2) \\\vec b=(-1,2)} \Rightarrow \vec a\cdot \vec b=3\cdot(-1)+2\cdot 2=-3+4=1,故選\bbox[red, 2pt]{(D)}$$
解答:$$相互平行的平面E_1與E_2,E_2上有無限多直線與E_1平行,故選\bbox[red, 2pt]{(E)}$$
解答:$$\overline{PQ}=|-4|= 4,故選\bbox[red, 2pt]{(C)}$$
解答:$$\cases{\overleftrightarrow{AB}在下平面ABCD\\ \overleftrightarrow{FG}在上平面EFGH} \Rightarrow 最短距離等於兩平面距離=\overline{CG}=2,故選\bbox[red, 2pt]{(A)}$$
解答:$${點數小於5且點數為偶數\over 點數為偶數} ={點數=2,4\over 點數=2,4,6} ={2\over 3},故選\bbox[red, 2pt]{(A)}$$
解答:$$抽中甲袋白球的機率+抽中乙袋白球的機率 ={1\over 2}\cdot {1\over 5}+{1\over 2}\cdot {2\over 5} ={3\over 10}=30\%,故選\bbox[red, 2pt]{(B)}$$
解答:$$2\begin{bmatrix} 1&-4\\ -1& 7\end{bmatrix}+ \begin{bmatrix}x& y\\z& w \end{bmatrix}= \begin{bmatrix} 2&-8\\ -2& 14\end{bmatrix}+ \begin{bmatrix}x& y\\z& w \end{bmatrix} =\begin{bmatrix} x+2 &y-8\\ z-2& w+14 \end{bmatrix}= \begin{bmatrix} 4&-3\\ -1& 2\end{bmatrix} \\ \Rightarrow y-8=-3 \Rightarrow y=5,故選\bbox[red, 2pt]{(E)}$$
解答:$$\begin{bmatrix} 3& 2\\ 0& 2\end{bmatrix} \begin{bmatrix}1\\3\end{bmatrix}= \begin{bmatrix} 3+6\\ 0+6 \end{bmatrix} = \begin{bmatrix} 9\\ 6 \end{bmatrix} ,故選\bbox[red, 2pt]{(C)}$$
解答:$$A=\begin{bmatrix} x& 3\\ 2& -6\end{bmatrix} , A^{-1}不存在 \Rightarrow \det(A)=0 \Rightarrow -6x-6=0 \Rightarrow x=-1,故選\bbox[red, 2pt]{(D)}$$
====================== END ==========================
解題僅供參考,其他運動績優試題及詳解


























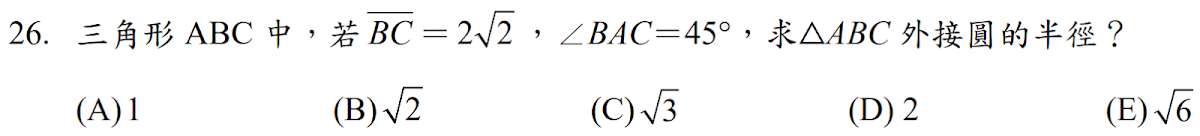














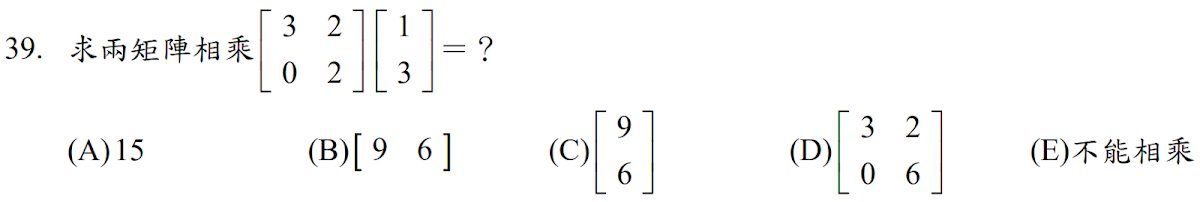



沒有留言:
張貼留言