GeoGebra 功能實在強大,可是大部份的人好像只是關注於中小學的數學,而且偏向函數繪圖。其實在大學數學上,GeoGebra 也提供了非常多的功能。今天先從微積分開始講起。
要講微積分,當然要先講「微分」。
↓起動GeoGebra的預設初始畫面
由於我們只是要講微分的功能,因此我們先將「繪圖」畫面收起來。
↓選《檢視》→《繪圖區》,將繪圖區關閉。
↓關閉繪圖區後的視窗,為了要講解方便,我們要將最下方的《輸入列》移到上方
↓點選《檢視》→《版面》
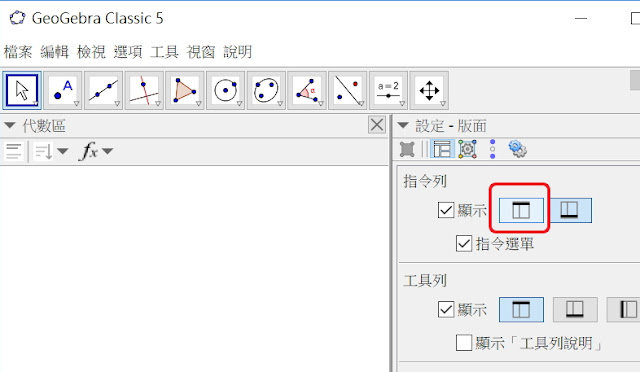
↓將指令列顯示在上方
↓版面設定後,指令列從下方移到上方,再點選《設定》畫面的叉叉,將設定版面關閉
↓設定完畢後的畫面
------------- 以上都是設定畫面 -------------- 正文從下方開始 ----------------------
直接從例子中開始....
假設 \(f(x)=2x^2-6x-3\),將此函數鍵入輸入列
↓輸入例輸入函數後,再《ENTER》鍵
如何求\(f(x)\)微分呢?很簡單,只要在輸入列鍵入《f'》即可
↓輸入f'後按《ENTER》
另一個比較難一點的方法就是使用GeoGebra 的函數 Derivative()。
↓Derivative 有六種選項
↓輸入 Derivative(f)後,再按《ENTER》
從以上兩種方法都可以求得\(\frac{d}{dx}f(x)=4x-6\)。
如果要微分兩次呢?方法一樣,一個是輸入f'';另一個使用函數 Derivative(f, 2)。
↓使用f'' 微分兩次
↓利用Derivative(f, 2),將f 微分兩次
↓輸入其它函數,利用 f', f'', f''' 分別求其一階、二階、三階的微分函數
如果是多變數函數就不能用一撇、兩撇來求微分,必須使用Derivative(函數名稱, 變數,微分次數)來求其微分。
↓利用Derivative(g,x,1)求\(\frac{\partial}{\partial x}g(x,y)\)
↓再對y微分,可得\(\frac{\partial^2}{\partial y\partial x}g(x,y)\)
如果函數中的係數是未知的,如:\(f(x)=ax^2+bx+c\),可不可以利用GeoGebra 求得\(f'(x) = 2ax+bx\)呢?答案當然是可以!只是要切換到GeoGebra的「運算區」!
↓選取《檢視》→《運算區》
↓將原來的代數區,按叉叉關閉
↓最後點選《檢視》→《指令列》,將指令列關閉
↓只有運算區的畫面
↓輸入Derivative(a*x^2+b*x+c, x),按《ENTER》可求得該式子對x的微分
在運算區(CAS)可以用這種指定變數的方法微分,在指令區就不能有未定係數。
另外,在原指令區利用函數求微分的方法,在運算區也是可以的。
↓運算區需用:= (冒號+等號),而且用f'(x)代表一次微分
↓幾個運算區求微分的例子
-- END --























沒有留言:
張貼留言