臺北市高級中等學校 102 學年度聯合轉學考招生考試
升高三數學科試題
升高三數學科試題
一、單選題
$$(A) \sin 320^\circ = \sin (360^\circ -40^\circ) = -\sin 40^\circ\\ (B) \sin 100^\circ = \sin (180^\circ -100^\circ) = \sin 80^\circ\\ (C) \tan (-135^\circ) = \tan 45^\circ=1\\ (D) \cos 90^\circ =0 \\(E) \cos 220^\circ =-\cos 40^\circ\\ 只有(A)與(E)是負值,又-\sin 40^\circ = -\cos 50^\circ > -\cos 40^\circ \Rightarrow (E)最小, 故選:\bbox[red,2pt]{(E)}$$
解:$$\begin{cases}\sin \alpha = 4/5 \\ \cos \beta = -5/13\end{cases} \Rightarrow \begin{cases} \cos \alpha = -3/5 \\ \sin \beta = -12/13\end{cases} \Rightarrow \sin (\alpha+\beta) = \sin \alpha \cos \beta + \sin \beta+ \cos \alpha \\ ={4\over 5}\times (-{5\over 13}) + (-{12 \over 13}) \times (-{3\over 5}) ={36-20 \over 65} = {16 \over 65}, 故選\bbox[red,2pt]{(B)}$$
解:
$$x^2+y^2 -2x+6y+k=0 \Rightarrow (x-1)^2+(y+3)^2 =10-k \Rightarrow 半徑=\sqrt {10-k}=2 \\ \Rightarrow 10-k=4 \Rightarrow k=6, 故選\bbox[red,2pt]{(E)}$$
解:$$\left( \vec a+t\cdot \vec b\right) \cdot \vec c=0 \Rightarrow ((1,-2) +t(4,1)) \cdot (2,-5) = (4t+1, t-2) \cdot (2,-5) = 8t+2-5t+10 \\ = 3t+ 12=0 \Rightarrow t=-4, 故選\bbox[red,2pt]{(D)}$$
解:
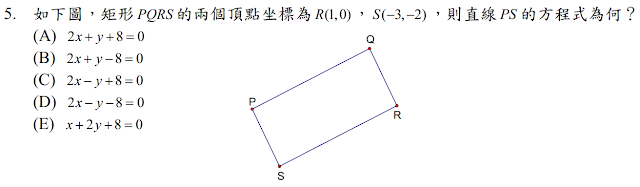
$$\begin{cases}R=(1,0) \\ S=(-3,-2) \end{cases} \Rightarrow \overline{RS}直線方程式 L:x-2y=1, \\由於\overline{RS} \bot \overline {PS} \Rightarrow \overline{PS}直線方程式M: 2x+y+k=0;\\ M經過點S(-3,-2) \Rightarrow -6-2+k=0 \Rightarrow k=8 \Rightarrow M: 2x+y+8=0, 故選\bbox[red,2pt]{(A)}$$
解:
$$直線ax-y=-3經過(0,3)且與直線\overline{AD}交於點P,見上圖\\ 又P為直線x+y=6與ax-y=-3的交點,因此P=({a+1 \over 3},{17-a \over 3}),再代入x+2y=11 \\\Rightarrow {a+1 \over 3}+ {34-2a \over 3}=11 \Rightarrow a=2, 故選\bbox[red,2pt]{(B)}$$
解:
解:$$假設六邊形邊長為a\\
(A) \overrightarrow{AB} \cdot \overrightarrow{AB} = a^2\\
(B) \overrightarrow{AB} \cdot \overrightarrow{AC} = a\times \sqrt 3a\times \cos 30^\circ ={\sqrt 3\over 2}a^2\\
(C) \overrightarrow{AB} \cdot \overrightarrow{AD} = a \times 2a \times \cos 60^\circ = a^2\\
(D) \overrightarrow{AB} \cdot \overrightarrow{AE} = a \times \sqrt 3a \times \cos 90^\circ =0\\
(E) \overrightarrow{AB} \cdot \overrightarrow{AF} = a \times a \times \cos 120^\circ = -{1\over 2}a^2\\,故選\bbox[red,2pt]{(E)} $$
解:
$$\begin{cases}P(1,-2,1) \\ Q(0,-1,2) \\ R(-3,-1,3) \\ S(k-1,k,k+1) \end{cases} \Rightarrow \begin{cases}\overrightarrow{PQ} = (-1,1,1) \\ \overrightarrow{PR} =(-4,1,2) \\ \overrightarrow{PS} =(k-2, k+2,k) \end{cases} \\\Rightarrow \overrightarrow{PQ} \times \overrightarrow{PR} = ( \begin{vmatrix}1 & 1 \\1 & 2 \end{vmatrix}, \begin{vmatrix}1 & -1 \\2 & -4 \end{vmatrix}, \begin{vmatrix}-1 & 1 \\-4 & 1 \end{vmatrix}) =(1,-2,3)\\ (\overrightarrow{PQ} \times \overrightarrow{PR}) \bot \overrightarrow{PS} \Rightarrow (\overrightarrow{PQ} \times \overrightarrow{PR}) \cdot \overrightarrow{PS}=0 \Rightarrow (1,-2,3) \cdot (k-2,k+2,k) = 2k-6=0 \\ \Rightarrow k=3,故選\bbox[red,2pt]{(C)} $$解:$$k=\overline{F_1F_2} =\sqrt{8^2+6^2}=10,故選\bbox[red,2pt]{(C)}$$
解:
$$(A)\times: A(B+C)=AB+AC \\(B) \times: (A+B)(A-B) = A^2-AB+BA-B^2 (AB不一定等於BA)\\ (C) \times: (AB)^3= ABABAB \ne A^3B^3 \\(D) \bigcirc: (\sqrt 2A)(\sqrt 3B)=\sqrt 6AB\\ (E) \times: \begin{bmatrix}1 & -1 \\1& -1 \end{bmatrix} \begin{bmatrix}1 & -1 \\1& -1 \end{bmatrix} =\begin{bmatrix}0 & 0 \\0& 0 \end{bmatrix} ,但 \begin{bmatrix}1 & -1 \\1& -1 \end{bmatrix} \ne 0\\,故選\bbox[red,2pt]{(D)}$$
解:
$$(A+B)(A-B)=A^2-B^2 \Rightarrow AB=BA \Rightarrow \begin{bmatrix}-1 & -2 \\ -3 & -4 \end{bmatrix} \begin{bmatrix}k & 2 \\3 & 1 \end{bmatrix} = \begin{bmatrix}k & 2 \\3 & 1 \end{bmatrix}\begin{bmatrix}-1 & -2 \\ -3 & -4 \end{bmatrix}\\ \Rightarrow \begin{bmatrix}-k-6 & -4 \\-3k-12 & -10 \end{bmatrix} = \begin{bmatrix}-k-6 & -2k-8 \\-6 & -10 \end{bmatrix} \Rightarrow \begin{cases} -2k-8=-4\\ -3k-12=-6 \end{cases} \Rightarrow k=-2,故選\bbox[red,2pt]{(A)}$$
二、多重選擇題
$$(A)\times: \vec a-\vec b=(5,12)-(-3,4) =(8,8) \\(B)\bigcirc: \vec a\cdot \vec b =(5,12)\cdot (-3,4) =-15+ 48 =33 \\ (C) \times: {|\vec a\cdot \vec b| \over |\vec b|} =33/5 \\(D) \bigcirc :\sqrt{|\vec a|^2|\vec b|^2 -(\vec a\cdot \vec b)^2} =\sqrt {13^2\times 5^2-33^2} =56 \\(E) \bigcirc: \cos \theta= {\vec a \cdot \vec b \over |\vec a||\vec b|} ={33 \over 13\times 5} ={33 \over 65} > {1\over 2}\\,故選\bbox[red,2pt]{(BDE)}$$
$$\begin{cases} \angle C=60^\circ \\ \angle D=135^\circ \end{cases} \Rightarrow \begin{cases} \angle A=180^\circ-\angle C=120^\circ \\ \angle B=180^\circ-\angle D=45^\circ \end{cases};又\overline{BD}的中垂線經過圓心O,如上圖;\\(A) \bigcirc: \triangle AED = 60^\circ-90^\circ-30^\circ \Rightarrow \overline{ED}= {\sqrt 3\over 2}\times \overline{AD} = \sqrt 3 \Rightarrow \overline{BD} =2\sqrt 3\\ (B) \times: \triangle AOB 為正\triangle \Rightarrow 半徑\overline{AO}=\overline{AB} =2\\ (C) \times: 等腰直角\triangle AOC \Rightarrow \overline{AC} =\sqrt 2\times \overline{AO}=2\sqrt 2\\ (D) \bigcirc: \angle ACB = \angle ADB (對同弧) = 30^\circ \\ (E) \times: \angle CAD = \angle CBD (對同弧) =15^\circ\\,故選\bbox[red,2pt]{(AD)}$$
17. 下列關於空間中的直線與平面的敘述何者正確?
(A) 兩不相交的直線必平行
(B) 相異的三點恰決定一平面
(C) 設直線 L與平面 E 恰交於一點 P ,若在平面E 上過 P 點的兩相異直線皆與 L垂直,則直線 L必垂直平面 E
(D) 若平面 E 與平面 F 皆垂直平面G ,則平面 E 與平面 F 必平行
(E) 平行於同一直線的兩相異直線必平行
解:
$$(A) \times: 可能歪斜\\(B) \times: 必須是不在一直線上的相異三點 \\ (D)\times: E、F也可能相互垂直\\其他皆正確,故選\bbox[red,2pt]{(CE)}$$
$$(A) \times: 可能歪斜\\(B) \times: 必須是不在一直線上的相異三點 \\ (D)\times: E、F也可能相互垂直\\其他皆正確,故選\bbox[red,2pt]{(CE)}$$
解:
$$\cfrac{x^2}{1} +\cfrac{(y+1)^2}{4}=4 \Rightarrow \cfrac{x^2}{4} +\cfrac{(y+1)^2}{16}=1 \Rightarrow \begin{cases}a = 4 \\b =2 \\ 中心(0,-1)\end{cases} \Rightarrow c= \sqrt{a^2-b^2} =2\sqrt 3\\(A) \times: 中心坐標(0,-1)\\(B) \times: 短軸長=2b=4\\(C) \bigcirc: 2c= 4\sqrt 3\\(D) \bigcirc: 2a=8\\ (E) \bigcirc:該四邊形為一菱形,面積=4\times {ab \over 2}=16\\,故選\bbox[red,2pt]{(CDE)} $$
19. 關於雙曲線\((2x-y-5)(2x+y-7)=16\),下列何者正確?
(A) 中心為(3,1)
(B) 貫軸所在直線為x=3
(C) 共軛軸所在直線為y=3
(D) 兩條漸近線斜率為\(\pm 2\)
(E) 中心到兩條漸進線的距離乘積為\({16\over 5}\)
解:$$(2x-y-5)(2x+y-7)=16 \Rightarrow 4x^2-24x-y^2+2y+19=0 \Rightarrow \cfrac{(x-3)^2}{4}- {(y-1)^2\over 16}=1\\(A) \bigcirc:中心為於(3,1)\\ (B) \times: 貫軸為y=1\\(C) \times: 共軛軸為x=3\\ (D) \bigcirc:漸近線4(x-3)=\pm 2(y-1) \Rightarrow 斜率為\pm 2 \\(E) \times: 兩條漸近線的交點為中心,因此距離的乘積為0\\,故選\bbox[red,2pt]{(AD)}$$
解題僅供參考


















沒有留言:
張貼留言