解:$$a+b=3 \Rightarrow b=3-a \Rightarrow ab=a(3-a)=1 \Rightarrow a^2-3a+1=0 \\\Rightarrow a=\cases{{3+\sqrt{5}\over 2} \\{3-\sqrt{5}\over 2}} \Rightarrow b=\cases{{3-\sqrt{5}\over 2} \\{3+\sqrt{5}\over 2}(不合,違反a>b)} \Rightarrow a-b={3+\sqrt{5}\over 2}-{3-\sqrt{5}\over 2}=\sqrt 5\\,故選\bbox[red, 2pt]{(D)}$$
解:$$\left| 5-{2\over x}\right| < 3 \Rightarrow -3< 5-{2\over x}<3 \Rightarrow -8< -{2\over x}<-2 \Rightarrow 2< {2\over x}< 8 \Rightarrow {1\over 4} < x < 1 \\ \Rightarrow a+b={1\over 4}+1 = {5\over 4},故選\bbox[red,2pt]{(B)}$$
解:$$108^{109}=a\times 108^{108}+108^{107}= 108^{107}(108a+1) \Rightarrow 108a+1=108^2 \Rightarrow a={108^2-1 \over 108} \\ \Rightarrow {1\over 107} ={108^2-1 \over 108\times 107}= {(108+1)(108-1) \over 108\times 107}= {109\times 107 \over 108\times 107} ={109\over 108},故選\bbox[red,2pt]{(B)}$$
解:$$\cases{a=\log 2\\ b=\log 3\\ c=\log 7} \Rightarrow 2a+b+c = 2\log 2+\log 3+\log 7 =\log (2^2\times 3\times 7) \\ \Rightarrow 10^{2a+b+c} =10^{\log (2^2\times 3\times 7)} =2^2\times 3\times 7=84,故選\bbox[red,2pt]{(D)}$$
5.設\(k\)為實數,平面上一直線\(L\)的方程式為\(y=kx+2k+3\),則\(L\)恆過的定點為何?
(A) (-2,3) (B) (2,3) (C) (2,-3) (D) (-2,-3)
解:$$y=kx+2k+3 \Rightarrow y(-2)=-2k+2k+3=3 \Rightarrow 恆過(-2,3),故選\bbox[red,2pt]{(A)}$$
6.設直線\(L\)與\(3x-4y=7\)垂直,且與平面座標軸在第一象限所圍成之三角形面積為6,則\(L\)的方程式為何?
\((A)4x+3y=-12\quad (B)4x-3y=12\quad (C)4x+3y=12\quad (D) 4x-3y=-12\)。
解:$$L與3x-4y=7垂直\Rightarrow L:4x+3y=k,與坐標軸交於(k/4,0)及(0,k/3) \\\Rightarrow \triangle 面積= {k\over 4}\times {k\over 3} \div 2=6 \Rightarrow k^2=144 \Rightarrow k=12(-12不合,\because \triangle 在第1象限)\\ \Rightarrow L:4x+3y=12,故選\bbox[red,2pt]{(C)}$$
解:$$x^2+y^2+2kx -4y+2k-2=0 \Rightarrow (x-k)^2+(y-2)^2=k^2-2k+6 \\\Rightarrow 圓半徑=\sqrt{k^2-2k+6}=3 \Rightarrow k^2-2k+6=9 \Rightarrow k^2-2k-3=0 \Rightarrow (k-3)(k+1) \\\Rightarrow k= -1(3不合,違反k<0),故選\bbox[red,2pt]{(C)}$$
解:$$令f(x)= x^3+x^2-x+15,依題意f(x)=0有一虛根1+2i \Rightarrow x=1+2i \Rightarrow (x-1)^2=(2i)^2 \\\Rightarrow x^2-2x+1=-4 \Rightarrow x^2-2x+5 為f(x)的因式,利用長除法可得f(x)=(x^2-2x+5)(x+3)\\ \Rightarrow f(x)=0的實根為-3,故選\bbox[red,2pt]{(D)}$$
解:$$f(x)=(x-{1\over 2})q(x)+r = 2(x-{1\over 2})\cdot {1\over 2}q(x)+r = (2x-1)\cdot {1\over 2}q(x)+r \\ \Rightarrow \cases{商式為{1\over 2}q(x) \\餘式仍為r},故選\bbox[red,2pt]{(B)}$$
解:
$$7^5-6\times 7^4+2\times 7^3-64\times 7^2+3\times 7-22 =7^4(7-6)+2\times 7^3-64\times 7^2+3\times 7-22 \\ =7^4 +2\times 7^3-64\times 7^2+3\times 7-22 =7^3(7 +2)-64\times 7^2+3\times 7-22 \\ = 9\times 7^3 -64\times 7^2+3\times 7-22 =7^2(9\times 7-64)+3\times 7-22 =-7^2+3\times 7-22 \\ =-49+21-22=-49-1=-50,故選\bbox[red,2pt]{(C)}$$
11. 已知一次函數f(x)滿足\(f(8)=3^8,f(k)=3^9,f(10)=3^{10}\),則\(k=\)?
(A) 9 (B) \({17 \over 2}\) (C) 8 (D) \({15\over 2}\)
12. 對於所有正整數 \(n\),若 \(2^{3n+2}+3\) 恆為質數\(P\)的倍數,則\(P\)值為何?
(A) 3 (B) 5 (C) 7 (D) 11。
解:
$$f(n)=2^{3n+2}+3 \Rightarrow \cases{f(1)=35 = 5\times 7 \\ f(2)=259= 7\times 37} \Rightarrow P=7,故選\bbox[red, 2pt]{(C)}$$
$$f(n)=2^{3n+2}+3 \Rightarrow \cases{f(1)=35 = 5\times 7 \\ f(2)=259= 7\times 37} \Rightarrow P=7,故選\bbox[red, 2pt]{(C)}$$
13. 人類的大拇指自指尖到腕骨是由三塊骨頭所組成。令從指尖到腕骨的這三塊骨頭的長度分別\(a_1、a_2、a_3\)。據統計,當\(a_1、a_2、a_3\)是等比數列且滿足\(a_3=a_1+a_2\)時,大拇指的型態被認為是最完美。求完美大拇指之三塊骨頭長度的公比\({a_2 \over a_1}\)為何?
\((A){\sqrt 5+1 \over 2}\quad (B){\sqrt 5-1 \over 2} \quad (C){\sqrt 5+1 \over 4}\quad (D){1-\sqrt 5 \over 2}\)。
解:$$a_1,a_2,a_3為等比 \Rightarrow \cases{a_2= a_1r\\ a_3= a_1r^2} \Rightarrow a_3=a_1+a_2 \Rightarrow a_1r^2=a_1+a_1r \Rightarrow r^2-r-1=0\\ \Rightarrow r={1+\sqrt 5\over 2}(負值不合,違反姆指長度為正值),故選\bbox[red, 2pt]{(A)}$$
14. 甲乙兩人比賽五子棋,約定每局比賽必分出勝負,但因乙是新手,約定只要甲勝3局前,乙能勝2局就算乙贏,否則算甲贏(即甲在乙勝2局前取得3勝)。則比賽共有多少種可能的情形?
(A) 10 (B) 11 (C) 12 (D) 13
解:$$比2局: 乙乙→乙勝\\ 比3局: 甲乙乙→乙勝, 乙甲乙→乙勝, 甲甲甲→甲勝\\ 比4局: (2甲1乙)甲→甲勝(排列數3), (2甲1乙)乙→乙勝(排列數3)\\,共有1+3+3+3=10種可能,故選\bbox[red, 2pt]{(A)}$$
15.阿華規劃一週七天晚上的其中三天讀數學,兩天讀英文,一天讀國文,剩一天晚上好好休息不讀書,則他每週晚上的安排方式有多少種?
(A) 60 (B) 120 (C) 210 (D) 420
解:$$此題相當於7個字-數數數英英國休-的排列數,即{7!\over 3!2!}=420,故選\bbox[red,2pt]{(D)}$$
解:$$(x-1)^9展開式中x^k的係數為C^9_k\times (-1)^{9-k} \Rightarrow x^5的係數C^9_5最大,故選\bbox[red,2pt]{(C)}$$
解:$$(1+2)^n= \sum_{k=0}^n2^kC^n_k = 1+2C^n_1+ 2^2C^n_2+\cdots +2^nC^n_n \Rightarrow 2C^n_1+ 2^2C^n_2+\cdots +2^nC^n_n=3^n-1 \\ \Rightarrow 243 \le 3^n-1< 729 \Rightarrow 244 \le 3^n < 730\Rightarrow n=6 (3^6=729),故選\bbox[red,2pt]{(B)}$$
18. 一組數據共有50筆資料,其中每一筆都只能是0或者1。若已知該組資料的標準差為0.48且0的個數比1的個數少,則資料裡的1共有多少個?
(A) 16 (B) 18 (C) 32 (D) 34
解:$$令50筆資料中,有a個1,且a>25 \Rightarrow EX= EX^2 ={a\over 50} \Rightarrow 標準差\sigma =\sqrt{EX^2-(EX)^2} \\ \Rightarrow 0.48 =\sqrt {{a\over 50} - {a^2\over 2500}} \Rightarrow {24^2 \over 2500} ={a\over 50} - {a^2\over 2500} \Rightarrow a^2-50a +576=0 \Rightarrow (a-32)(x-18)=0 \\\Rightarrow a=32 (18不合,違反a>25),故選\bbox[red,2pt]{(C)}$$
解:$$\cases{買到1個不良品的機率= {C^4_2C^2_1 \over C^{6}_3} ={3\over 5} \\ 買到2個不良品的機率= {C^4_1C^2_2 \over C^{6}_3} ={1\over 5} } \Rightarrow 期望值=1\times {3\over 5} +2\times {1\over 5} =1,故選\bbox[red, 2pt]{(D)}$$
解:
$$\angle A=100^\circ \Rightarrow \angle B=\angle C=(180-100)\div 2=40^\circ ;\\又D為\overline{BC}的中點 \Rightarrow \overline{CD}= {1\over 2}\overline{BC} =1 \Rightarrow \overline{AD} = \overline{CD}\times \tan \angle C = \tan 40^\circ,故選\bbox[red, 2pt]{(A)}$$
21. 設\(a、b、c\)表示\(\triangle ABC\)的三邊長,且滿足\(a^2+b^2+c^2-ab-bc-ca=0\),若\(\triangle ABC\)的周長為18,則\(\triangle ABC\)的面積為何?
(A) \(9\sqrt 3\) (B) \(12\sqrt 3\) (C) \(15\sqrt 3\) (D) 條件不足,無法判斷
解:$$a^2+b^2+c^2 -ab-bc-ca=0 \Rightarrow 2a^2+2b^2 +2c^2 -2ab-2bc-2ca=0 \\\Rightarrow (a-b)^2 +(b-c)^2 +(c-a)^2=0 \Rightarrow a=b=c\\ 又a+b+c=18 \Rightarrow a=b=c=6 \Rightarrow 正\triangle 面積= 6\times 3\sqrt 3\div 2=9\sqrt 3,故選\bbox[red,2pt]{(A)}$$
解:$$P(\sin \theta, \tan \theta)在第2象限\Rightarrow \cases{\sin \theta< 0\\ \tan \theta>0}\Rightarrow \cases{\sin \theta< 0\\ \cos \theta <0} \Rightarrow \theta 在第3象限,故選\bbox[red,2pt]{(C)}$$
解:$$\triangle ABC面積={1\over 2}\overline{AB}\times \overline{AC} \sin \angle A= 3\sin \angle A \Rightarrow \sin \angle A越小則面積越小\\ \cases{(A) \angle 78^\circ \\ (B) \sin 96^\circ = \sin 84^\circ \\ (C)\sin 120^\circ = \sin 60^\circ \\(D) \sin 132^\circ = \sin 48^\circ },故選\bbox[red,2pt]{(D)}。$$
解:$$\cos 60^\circ = {\overline{AB}^2 +\overline{AC}^2 -\overline{BC}^2 \over 2\times \overline{AB}\times \overline{AC}} \Rightarrow {1\over 2}= {64 +\overline{AC}^2 -49 \over 16 \overline{AC}} \Rightarrow \overline{AC}^2-8\overline{AC}+15=0 \\ \Rightarrow (\overline{AC}-5)(\overline{AC}-3)=0 \Rightarrow \overline{AC}=5\;或\;3 \Rightarrow 5+3=8,故選\bbox[red,2pt]{(C)}$$
解:$$(x^2+y^2+(x-2y+6)^2)((-1)^2+2^2+1^2) \ge (-x+2y+x-2y+6)^2 \\ \Rightarrow (x^2+y^2+(x-2y+6)^2)\times 6 \ge 6^2 \Rightarrow x^2+y^2+(x-2y+6)^2 \ge 6,故選\bbox[red,2pt]{(A)}$$
解:$$\cases{A(1,-2) \\B(3,1) \\C(0,-1) \\D(6,-2)} \Rightarrow \cases{\overrightarrow{AD} = (5,0) \\ \overrightarrow{AB} =(2,3) \\ \overrightarrow{AC} =(-1,1)} \Rightarrow \overrightarrow{AD} =x\overrightarrow{AB} +y\overrightarrow{AC} \Rightarrow (5,0) =(2x-y, 3x+y) \\ \Rightarrow \cases{2x-y=5 \\ 3x+y=0} \Rightarrow \cases{x=1 \\ y=-3},故選\bbox[red,2pt]{(B)}$$
解:$$A\left[\matrix{7 & 9 \\ 3 & 4} \right] =\left[\matrix{a & b \\ c & d} \right] \Rightarrow \cases{A\left[\matrix{7 \\ 3 } \right] =\left[\matrix{a \\ c }\right] =\left[\matrix{2 \\ 1 }\right]\\ A\left[\matrix{9 \\ 4 } \right] =\left[\matrix{b \\ d }\right] =\left[\matrix{1 \\ 5 }\right]} \Rightarrow a+b+c+d =2+1+1+5=9\\,故選\bbox[red,2pt]{(D)}$$
解:$$\left[\matrix{3+a & 4 \\ 2 & 1+a} \right] \left[\matrix{x \\ y} \right] =\left[\matrix{2 \\ 1} \right] \Rightarrow \cases{ (3+a)x+4y=2 \\ 2x+(1+a)y=1 } ; 無限多解\Rightarrow {3+a\over 2}={4\over 1+a}={2 \over 1} \\\Rightarrow a=1,故選\bbox[red,2pt]{(B)}$$
解:
$$y^2=8x=4\times 2x \Rightarrow \cases{O(0,0)為頂點\\ (2,0)=B為焦點 \\ L:x=-2 為準線} \Rightarrow 依拋物線定義\overline{PB}= \text{dist}(P,L) \\\Rightarrow \overline{PA}+ \overline{PB}= \overline{PA}+ \overline{PB'},B'在準線上(如上圖左)\\ \Rightarrow B',P,B三點在一直線上時(如上圖右),\overline{PA}+ \overline{PB}最小\\ \Rightarrow 此時\overline{PA}+ \overline{PB} = \overline{B'A} = 5-(-2)=7,故選\bbox[red, 2pt]{(C)}$$
解:
$${x^2 \over 25} +{y^2 \over 2}=1 \Rightarrow \cases{中心點O(0,0)\\ a=5 \\ b=\sqrt 2} \Rightarrow 橢圓上的點P,\sqrt 2 \le \overline{OP} \le 5 \Rightarrow \overline{OP}的整數值可為5,4,3,2;\\ \Rightarrow \cases{\overline{OP}=5 \Rightarrow 左右2頂點符合 \\ \overline{OP}=2,3,4 \Rightarrow 各有4個點符合} \Rightarrow 共有2+4\times 3=14個點,故選\bbox[red, 2pt]{(A)}$$
解:$$(A)\bigcirc: \sqrt 3是無理數\Rightarrow 2+\sqrt 3也是無理數\\ (B) \bigcirc: \sqrt{7+\sqrt {48}} =\sqrt{7+4\sqrt 3} =\sqrt{(2+\sqrt 3)^2} =2+\sqrt 3 \\(C)\times: \sqrt 3=1.732 \Rightarrow \sqrt 3的小數部分是\sqrt 3-1 \Rightarrow 2+\sqrt 3的小數部分也是\sqrt 3-1 \ne 2-\sqrt 3 \\(D)\bigcirc: x=\sqrt 3-1 \Rightarrow (x+1)^2 = (\sqrt 3)^2 \Rightarrow x^2+2x= 2\Rightarrow x^2+4x=2+2x= 2+2(\sqrt 3-1) =2\sqrt 3\\ (E) \bigcirc: \cases{(\sqrt{2+\sqrt 3 })^2 = 2+\sqrt 3\\ 2^2=4} \Rightarrow 2^2-(\sqrt{2+\sqrt 3 })^2 =2-\sqrt 3 >0 \Rightarrow \sqrt{2+\sqrt 3} < 2\\,故選\bbox[red, 2pt]{(ABDE)}$$
解:$$(A)\times: b=4^{0.05}= 2^{0.1} \Rightarrow 2b=2^{1.1} \ne a \\(B)\bigcirc: b=4^{0.05}= 2^{0.1} \Rightarrow b^2=(2^{0.1})^2= 2^{0.2} =a \\(C)\times: a+b=2^{0.2}+4^{0.05} =2^{0.2}+2^{0.1} \ne 2^{0.3} \\(D) \bigcirc: a\times b=2^{0.2}\times 2^{0.1} =2^{0.3} \\(E)\bigcirc: {a\over b} ={2^{0.2}\over 2^{0.1}} =2^{0.1}\\,故選\bbox[red,2pt]{(BDE)}$$
解:
$$(A),(B),(D)的反例如上圖,故選\bbox[red,2pt]{(CE)}$$
解:$$(C) \times: \pi = 3.14 > 4 \\(D)\times: 3是奇數不是偶數\\ 其他皆正確,故選\bbox[red,2pt]{(ABE)}$$
解:$$(B) \bigcirc: b=(a-2)^3 \Rightarrow -b=(2-a)^3 = ((4-a)-2)^2 \Rightarrow (4-a,-b)也在y=(x-2)^3上 \\(C)\bigcirc: 0=(2-2)^2 \Rightarrow (2,0)在y=(x-2)^3上\\其他點都不在y=(x-2)^3上,故選\bbox[red, 2pt]{(BC)}$$
解:$$(A) \bigcirc:x^2+x+1= (x+{1\over 2})^2+ {3\over 4} \ge {3\over 4} \not \lt 0 \\(B) \times: x^2+3x-1 = (x+{3\over 2})^2-{13\over 4} >0 有實數解\\(C) \bigcirc: x^2-2x+3= (x-1)^2+2 \ge 2 \not\le 0 \\(D) \times: -x^2+4x-4= -(x-2)^2\ge 0 \Rightarrow x=2 \\(E) \times: -x^2-2x+3 =-(x+1)^2+4 >0有實數解\\,故選\bbox[red,2pt]{(AC)}$$
解:$$(A)\times: 100-999共有999-99=900個 \\(B)\bigcirc: 9\times 9 \times 8 =648 \\(C)\bigcirc: 2XX有9\times 9=81個,X2X有8\times 9=72個,XX2有8\times 9=72個\\\qquad,因此共有81+2\times 72=225個\\ (D)\bigcirc: 數字2完全不出現的三位數有8\times 9\times 9=648個,全部900-沒有2的648=252\\ (E)\bigcirc: 三個3只有1個(333),二個3:33X(9個,不含333),3X3(9個,不含333),X33(8個,不含333)\\\qquad,共有1+9+8+8=27個,故選\bbox[red,2pt]{(BCDE)}$$
解:$$迴歸直線L方程式:y-\mu_y=m(x-\mu_x),其中m=r_{xy}\times {\sigma_y \over \sigma_x} =0.75\times {2\over 3}=0.5 \\ \Rightarrow L: y-6=0.5(x-5) \Rightarrow L:x-2y+7=0 \\(A)\times1-4+7\ne 0 \\(B) \bigcirc:3-10+7=0 \\(C)\times: 6-10+7\ne 0 \\(D)\times: 8-14+7 \ne 0 \\(E) \bigcirc: 9-16+7=0\\,故選\bbox[red,2pt]{(BE)}$$
解:$$(A)\bigcirc: \sum_{k=1}^{109} 109 = 109\times 109 = 109^2 \\(B) \times:\sum_{k=1}^{109} k={(109+1)109 \over 2} ={109\times 110\over 2} \ne {108\times 109\over 2} \\(C)\times: \sum_{k=3}^{109}2^k = {2^3-2^{110}\over 1-2} = {8(2^{107}-1)\over 2-1} \ne {8(2^{106}-1)\over 2-1}\\ (D)\bigcirc: 令u=t+1 \Rightarrow \sum_{t=1}^{108}(t+1)^3 = \sum_{u=2}^{109}u^3 =\sum_{k=2}^{109}k^3 \\(E)\times: \sum_{k=1}^{109} {1\over k(k+1)} =\sum_{k=1}^{109} ({1\over k}-{1\over k+1}) = 1-{1\over 110} ={109\over 110} \ne {108\over 109}\\,故選\bbox[red,2pt]{(AD)}$$
解:$$向量(a,b)與(c,d)所張成的\triangle 面積S={1\over 2}\sqrt{(a^2+b^2)(c^2+d^2)-(ac+bd)^2} \\={1\over 2}\sqrt{a^2c^2+a^2d^2 +b^2c^2+b^2d^2 -a^2c^2-2abcd-b^2d^2} ={1\over 2}\sqrt{a^2d^2 +b^2c^2-2abcd}\\(A)\bigcirc:向量(b,d)與(a,c)所張成的\triangle 面積={1\over 2}\sqrt{(b^2+d^2)(a^2+c^2)-(ab+cd)^2} \\ ={1\over 2}\sqrt{a^2b^2+b^2c^2+a^2d^2 +c^2d^2 -a^2b^2-2abcd-c^2d^2} ={1\over 2}\sqrt{a^2d^2 +b^2c^2-2abcd}=S \\(B)\times: 向量(b,a)與(c,d)所張成的\triangle 面積={1\over 2}\sqrt{(b^2+a^2)(c^2+d^2)-(bc+ad)^2} \\ ={1\over 2}\sqrt{b^2c^2+b^2d^2 +a^2c^2+a^2d^2 -b^2c^2-2abcd-a^2d^2} ={1\over 2}\sqrt{a^2c^2+b^2d^2-2abcd}\ne S \\(C)\times: 向量(2a,{b\over 3})與(18c,3d)所張成的\triangle 面積 ={1\over 2}\sqrt{(4a^2+ {b^2\over 9})(324c^2+9d^2)-(36ac+bd)^2} \\ ={1\over 2}\sqrt{36a^2c^2+36a^2d^2 +36b^2c^2+b^2d^2-36a^2c^2-72abcd-b^2d^2} ={1\over 2}\sqrt{36a^2d^2 +36b^2c^2-72abcd} \\=3\sqrt{a^2d^2 +b^2c^2-2abcd} =6S \\(D) \times:向量(a+b,a-b)與(c+d,c-d)所張成的\triangle 面積 ={1\over 2}\sqrt{(2a^2+2b^2)(2c^2+2d^2)-(2ac+2bd)^2} \\={1\over 2}\sqrt{4a^2d^2 +4b^2c^2-8abcd} =2S \\(E)\bigcirc: 向量(a+2b,b)與(c+2d,d)所張成的\triangle 面積 \\={1\over 2}\sqrt{(a^2+4ab+5b^2)(c^2+4cd+ 5d^2)-(ac+2ad+2bc+5bd)^2} \\={1\over 2}\sqrt{a^2d^2 +b^2c^2-2abcd} =S\\,故選\bbox[red,2pt]{(AE)}$$
-- END --

































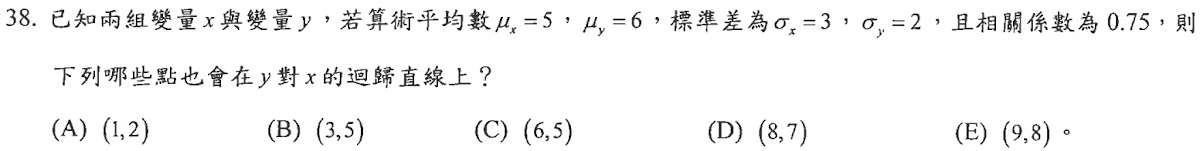


嗨~~不好意思 第37題的(E)是數字3不是數字2
回覆刪除謝謝提醒,已修訂!!!
刪除作者已經移除這則留言。
回覆刪除不好意思19題買到1個不良品的分母應該是C4取2*C2取1,2個不良品是C4取1*C2取2
回覆刪除謝謝提醒, 已修訂完畢!!!
刪除