臺灣警察專科學校專科警員班二十八期(正期學生組)
新生入學考試甲組數學科試題
新生入學考試甲組數學科試題
壹、單選題
解:$$(\log_2 3)\cdot (\log_3 7)\cdot (\log_7 8)= {\log 3\over \log 2} \times {\log 7\over \log 3} \times {\log 8\over \log 7} = {\log 8 \over \log 2} =\log_2 8 =3,故選\bbox[red,2pt]{(C)}$$
解:$$\cos 1590^\circ =\cos (360^\circ \times 4+ 150^\circ) =\cos 150^\circ =- \cos 30^\circ =-{\sqrt 3\over 2} ,故選\bbox[red,2pt]{(D)}$$
解:$$令s= (\overline{AB} +\overline{BC} +\overline{AC})\div 2= (5+6+7)\div 2 =9 \\\Rightarrow \triangle ABC面積= \sqrt{s(s-\overline{AB})(s-\overline{BC}) (s-\overline{AC})} = \sqrt{9(9-5)(9-6)(9-7)}\\ =\sqrt{9\times 4\times 3\times 2} =6\sqrt 6,故選\bbox[red,2pt]{(B)}$$
解:
$$\cases{(A)\log_2 7 >0 \\(B) \log_3 7>0 \\(C) \log_{0.2} 7 = {\log 7 \over \log 0.2} = {\log 7 \over {\log 2-\log 10}}= {\log 7 \over \log 2 -1}<0 \\(D) \log_{0.3}7= {\log 7 \over \log 3-1}<0} ,又 \log_2 7>\log_3 7 ,因此(A)最大,故選\bbox[red,2pt]{(A)}$$
解:$$與圓相切代表圓心(0,0)至直線的距離等於圓半徑長(5),只有(B)符合此條件,故選\bbox[red,2pt]{(B)}$$
解:$$球S:x^2+y^2+z^2=49 \Rightarrow \cases{球心O(0,0,0)\\ 球半徑R=7} \Rightarrow a=\text{dist}(O,E)= \left| { 12\over \sqrt{2^2 +1^2 +(-2)^2}} \right| =4\\ 令圓半徑r \Rightarrow R^2=r^2+a^2 \Rightarrow 49= r^2+16 \Rightarrow r^2=33 \Rightarrow 圓面積= r^2\pi =33\pi,故選\bbox[red,2pt]{(D)}$$
解:
$$令A為原點,各點坐標如上圖 \Rightarrow \cases{A(0,0,0) \\B(2,0,0) \\D(0,3,0) \\ E(0,0,3)} \Rightarrow \cases{\overrightarrow{AB}= (2,0,0) \\ \overrightarrow{AD}= (0,3,0) \\ \overrightarrow{EB}= (2,0,-3) \\\overrightarrow{ED}= (0,3,-3)} \\\Rightarrow \cases{\vec u= \overrightarrow{AB} \times \overrightarrow{AD} =(0,0,6)\\\vec v= \overrightarrow {EB} \times \overrightarrow{ED} =(9,6,6)} \\ \Rightarrow \cos \theta = {\vec u\cdot \vec v \over |\vec u||\vec v|} = {36 \over 6\times 3\sqrt{17}} ={2\over \sqrt{17}} \Rightarrow \sin \theta= {\sqrt{13} \over \sqrt{17}},故選\bbox[red,2pt]{(D)}$$
解:$$\left| 4\times 2-3\times 3+6\over \sqrt{4^2+(-3)^2} \right| ={5\over 5}=1,故選\bbox[red,2pt]{(A)}。 $$
解:$$\overrightarrow{AP} = x\overrightarrow {AB}+y\overrightarrow{AC} =\cases{2\overrightarrow{AD} +y\overrightarrow{AC} \\x\overrightarrow{AB} + {3\over 2}\overrightarrow{AE}} \Rightarrow \cases{2x+y=1 \\ x+{3\over 2}y=1} \Rightarrow \cases{x=1/4 \\y=1/2},故選\bbox[red,2pt]{(C)}。$$
解:
$$1={180^\circ \over \pi} \Rightarrow \cases{\sin 1=\sin {180^\circ \over \pi} \approx \sin 57^\circ \\ \sin 2=\sin{2\times 180^\circ \over \pi} \approx \sin 114^\circ =\sin 66^\circ \\ \sin 3= \sin{3\times 180^\circ \over \pi} \approx \sin 171^\circ =\sin 9^\circ \\\sin 4= \sin {4\times 180^\circ \over \pi} \approx \sin 228^\circ <0} \Rightarrow \sin 2最大,故選\bbox[red, 2pt]{(B)}$$
解:$$由題意意知: \cases{a_1+2b_1+3c_1 =d_1 \\ a_2+2b_2+3c_2 =d_2 \\a_3+2b_3+3c_3 =d_3 } \Rightarrow \cases{a_1\cdot 4+2b_1 \cdot 4+3c_1\cdot 4 =4d_1 \\ a_2\cdot 4 +2b_2\cdot 4 +3c_2\cdot 4 =4d_2 \\a_3\cdot 4+2b_3\cdot 4 +3c_3\cdot 4 =4d_3 } \\ \Rightarrow (4,4,4)是\cases{a_1x+2b_1y+3c_1z =4d_1 \\ a_2x+2b_2y+3c_2 z=4d_2 \\a_3x+2b_3y+3c_3z =4d_3 } 的解,故選\bbox[red, 2pt]{(D)}$$
解:$$\begin{vmatrix} 1 & -2 & 3\\ 2 & 1 &-5 \\ a & -5 & 4\end{vmatrix} =0 \Rightarrow 4-30+10a-3a+16-25=0 \Rightarrow a=5,故選\bbox[red, 2pt]{(D)}$$
解:
$$此題相當於求兩圖形\cases{y=3\sin x \\y=x}的交點數量;\\令A_k為y=3\sin x在第一象限的極大值坐標,即A_k=({\pi \over 2}+2k\pi,3),k=0,1,2,\dots\\,則直線\overline{OA_k}的斜率m_k={3\over {\pi \over 2}+2k\pi}\\ \Rightarrow \cases{m_0 = {6 \over \pi} > 1 \\ m_1={6\over 5\pi}< 1\\ 直線y=x的斜率m=1} \\\Rightarrow m_1 < m< m_0 \Rightarrow 兩圖形在第1象限有一個交點;\\由於兩圖形皆過原點且對稱原點,因此在第3象限也有一個交點,總共有3個交點,故選\bbox[red,2pt]{(A)}。$$
解:
$$\tan \alpha ,\tan \beta 為x^2+5x+2=0的兩根\Rightarrow \cases{\tan\alpha +\tan \beta=-5 \\ \tan\alpha \tan \beta=2} \\ \Rightarrow \tan(\alpha+\beta) ={\tan \alpha + \tan \beta\over 1-\tan \alpha\tan\beta} = {-5\over -1}=5 \Rightarrow \cases{\sin(\alpha+\beta)={5\over \sqrt{26}} \\ \cos(\alpha+\beta)={1\over \sqrt{26}}} \\ \Rightarrow \sin^2(\alpha+\beta) +4\sin(\alpha+\beta) \cos(\alpha+\beta) +7\cos^2(\alpha+\beta)= {25\over 26} +{20\over 26}+{7\over 26}= {52 \over 26}=2\\,故選\bbox[red,2pt]{(B)}。$$
解:$$f(x)= \sqrt 3\sin x-\cos x+1 =2({\sqrt 3\over 2} \sin x-{1\over 2}\cos x)+1 = 2(\cos y\sin x-\sin y\cos x)+1 \\ =2\sin(x-y)+1 \Rightarrow -1 \le f(x) \le 3,故選\bbox[red,2pt]{(C)}$$
解:$$a={2+2i \over 1+\sqrt 3 i} \Rightarrow a^2 =\sqrt 3-i \Rightarrow a^4=2-2\sqrt 3i \Rightarrow a^8=-8-8\sqrt 3i \Rightarrow \\a^{12}=(2-2\sqrt 3i)(-8-8\sqrt 3i) =-64,故選\bbox[red,2pt]{(D)}$$
解:$$\cases{取得1元的機率={10\over 10+6+4} ={1\over 2} \\ 取得5元的機率={6\over 10+6+4} ={3 \over 10} \\取得10元的機率={4\over 10+6+4} ={2 \over 10} } \Rightarrow 期望值=1\times {1\over 2}+ 5\times {3\over 10} + 10\times {2\over 10}=4,故選\bbox[red, 2pt]{(D)}$$
解:$$\cases{3球皆白球的機率=C^3_3/C^{12}_3 \\3球皆黑球的機率=C^4_3/C^{12}_3 \\3球皆紅球的機率=C^5_3/C^{12}_3 } \Rightarrow 3球皆同色的機率=(C^3_3 +C^4_3 +C^5_3)/C^{12}_3 = {15 \over 220} = {3\over 44}\\,故選\bbox[red,2pt]{(B)}$$
解:$$\log 12^{100} = 100\log 12=100(\log 3+2\log 2) = 100(0.4771+0.602)=107.91 \\\Rightarrow 它是107+1=108位的正整數,故選\bbox[red,2pt]{(B)}$$
解:
$$利用柯西不等式: (x^2+y^2+z^2)(6^2+2^2+3^2) \ge (6x+2y+3z)^2 \Rightarrow 9\times 49 \ge (6x+2y+3z)^2 \\ \Rightarrow -21 \le 6x+2y+3z \le 21 \Rightarrow 最大值為21,故選\bbox[red,2pt]{(C)}$$
解:$$x^2+2x+7 = (x+1)^2+6 \ge 6 \Rightarrow (x^2+2x+7)(x+1)(x+2)< 0 \Rightarrow (x+1)(x+2) < 0\\ \Rightarrow -2 < x< -1,故選\bbox[red,2pt]{(A)}$$
解:$$A= \begin{bmatrix}3 & 5 \\ 1& 2 \end{bmatrix} \Rightarrow det(A)=6-5=1 \Rightarrow A^{-1}=\begin{bmatrix}2 & -5 \\ -1& 3 \end{bmatrix} =\begin{bmatrix}a & b \\ c& d \end{bmatrix} \Rightarrow \cases{c=-1 \\ d=3} \\\Rightarrow c+d= -1+3= 2,故選\bbox[red,2pt]{(A)}$$
解:$${ 支持廢除死刑且無政黨傾向的比率\over 支持廢除死刑的比率} = {0.2\times 0.4 \over 0.4\times 0.6 + 0.4\times 0.2 + 0.2\times 0.4} ={0.08\over 0.4} =0.2 ={1\over 5}\\,故選\bbox[red,2pt]{(B)}。$$
解:$${(1,0,1),(1,1,0),(0,1,1) \over 全部-(0,0,0)} ={ 3\over 8-1} ={3\over 7},故選\bbox[red,2pt]{(C)}$$
解:
$$P為底面正六邊形的中心原點,正六邊形面積=6個正\triangle 面積= 6\times \triangle PAB\\ =6\times \left(r\times {\sqrt 3\over 2}r \times {1\over 2} \right) ={3\sqrt 3\over 2}r^2\\在直角\triangle APO \Rightarrow \overline{OP} =\sqrt{\overline{OA}^2-\overline{AP}^2} =\sqrt{36-r^2} \Rightarrow 正六角錐體積{1\over 6}\times {3\sqrt 3\over 2}r^2 \times \sqrt{36-r^2} \\ ={\sqrt 3\over 4}r^2\sqrt{36-r^2} ={\sqrt 3\over 4}\sqrt{36r^4-r^6};令f(r)=36r^4-r^6\Rightarrow f'(r)=144r^3-6r^5 =6r^3(24-r^2) \\ \Rightarrow r^2=24時,f(r)有極大值,即r=\sqrt{24}=2\sqrt 6,故選\bbox[red,2pt]{(D)}$$
解:$$A= \begin{bmatrix} 1 & 0 & 0\\ 0 & 3 & 0 \\ 0 & 0 & 2\end{bmatrix} \Rightarrow A^3=\begin{bmatrix} 1^3 & 0 & 0\\ 0 & 3^3 & 0 \\ 0 & 0 & 2^3\end{bmatrix} =\begin{bmatrix} 1 & 0 & 0\\ 0 & 27 & 0 \\ 0 & 0 & 8\end{bmatrix} \Rightarrow b=27,故選\bbox[red, 2pt]{(D)}$$
解:$$\cases{\vec u=\overrightarrow{AB} =(-1,0,3) \\ \vec v=平面7x+4y-4z=0的法向量=(7,4,-4)} \Rightarrow \vec n= \vec u\times \vec v =(-1,0,3) \times (7,4,-4)\\ =(-12,17,-4) \Rightarrow E: 法向量為\vec n且過A(2,1,-1) \Rightarrow E: -12(x-2)+17(y-1)-4(z+1)=0\\ \Rightarrow 12x-17y+4z-3=0,故選\bbox[red,2pt]{(B)}$$
解:$$y=f(x)=x^3-6x^2+9x-2 \Rightarrow f'(x)=3x^2-12x+9 \Rightarrow f''(x)=6x-12 \\ \Rightarrow f''(x)=0 \Rightarrow 6x-12=0 \Rightarrow x=2 \Rightarrow 反曲點(2,f(2))= (2,0),故選\bbox[red,2pt]{(C)}$$
解:$$R=\int_1^2 f(x)\;dx= \int_1^2 x^2\;dx = \left. \left[ {1\over 3}x^3\right] \right|_1^2 ={1\over 3}(8-1)= {7\over 3},故選\bbox[red,2pt]{(C)}$$
解:$$\int_0^1 f^2(x)\pi\;dx = \pi\int_0^1 x\;dx = {\pi \over 2},故選\bbox[red,2pt]{(A)}$$
貳、多重選擇題
解:$$\omega= \cos{2\pi \over 5} +i \sin{2\pi \over 5} \Rightarrow \omega^5= \cos 2\pi+i\sin 2\pi =1\\ (A)\times: \omega^5=1 \Rightarrow \omega^5-1=0 \Rightarrow (\omega-1)(\omega^4+ \omega^3+ \omega^2+ \omega+1)=0 \Rightarrow \omega^4+ \omega^3+ \omega^2+ \omega+1=0 \\\qquad \Rightarrow \omega^4+ \omega^3+ \omega^2+ \omega=-1 \ne 1\\(B)\bigcirc: \omega^5=1 \Rightarrow \omega^{10}=1 \\(C) \times: (1-\omega)(1-\omega^4)(1-\omega^2)(1-\omega^3) =(1-\omega-\omega^4+\omega^5) (1-\omega^2-\omega^3+\omega^5) \\ \qquad =(2-\omega-\omega^4)(2-\omega^2-\omega^3)=4-2\omega^2-2\omega^3-2\omega+\omega^3+ \omega^4-2\omega^4 +\omega^6+\omega^7 \\ \qquad = 4-2\omega-2\omega^2-\omega^3-\omega^4+\omega^6+\omega^7 = 4-2\omega-2\omega^2-\omega^3-\omega^4+\omega+\omega^2 \\\qquad =4-\omega-\omega^2-\omega^3-\omega^4=4-(-1)=5 \ne 1 \\(D) \bigcirc: (1+\omega)(1+\omega^4)(1+\omega^2)(1+\omega^3) = (1+\omega+\omega^4 +1) (1+\omega^2 +\omega^3+1) \\\qquad =(2+\omega +\omega^4)(2+\omega^2+\omega^3) = 4+2\omega +2\omega^2+3\omega^3 +3\omega^4+\omega^6+ \omega^7 \\\qquad =4 +3(\omega+\omega^2+\omega^3+\omega^4) = 4+3\times (-1) =1\\(E) \times: {1\over 1+\omega} +{1\over 1+\omega^2} +{1\over 1+\omega^3} +{1\over 1+\omega^4} \\\qquad = {(1+\omega^2)(1+\omega^3)(1+\omega^4)+ (1+\omega) (1+\omega^3)(1+\omega^4) +(1+\omega) (1+\omega^2)(1+\omega^4) +(1+\omega) (1+\omega^2)(1+\omega^3)\over (1+\omega) (1+\omega^2)(1+\omega^3)(1+\omega^4)} \\\qquad =(1+\omega^2)(1+\omega^3)(1+\omega^4)+ (1+\omega) (1+\omega^3)(1+\omega^4) +(1+\omega) (1+\omega^2)(1+\omega^4) +(1+\omega) (1+\omega^2)(1+\omega^3) \\ \qquad = (2+\omega^2+\omega^3)(1+\omega^4) +(2+\omega+\omega^4)(1+\omega^3)+ (2+\omega+\omega^4)(1+\omega^2)+ (2+\omega^2+\omega^3)(1+\omega)\\\qquad =(2+\omega^2+\omega^3)(2+\omega+\omega^4)+(2+\omega+\omega^4)(2+\omega^2+\omega^3)\\ \qquad =2(2+\omega^2+\omega^3)(2+\omega+\omega^4) =2(4+3(\omega+\omega^2+\omega^3+\omega^4))= 2(4-3)=2 \ne 1\\,故選\bbox[red,2pt]{(BD)}$$
解:
$$y=\log_2 x\;圖形只經過一、四象限,為一遞增函數 \\(A)\bigcirc: y=2為一水平線,與y=\log_2 x交於(4,2) \\ (B) \bigcirc: x+y=2為左上右下直線,與遞增圖形只會交於一點\\ (C)\times: \log_2 x=x+2 \Rightarrow 4\times 2^x =x \Rightarrow 無解,即無交點\\ (D) \times: 2^x > \log_2 x \Rightarrow 兩圖形不會有交點 \\(E) \bigcirc: \log_{0.5} x=-\log_2 x \Rightarrow 兩圖形對稱於X軸,即上下對稱,並交於(1,0)\\,故選\bbox[red,2pt]{(ABE)}$$
解:$$(A) \times: z=3為一平面 \\(B) \times: 2x+3y=6為一平面 \\(C) \bigcirc: {x-3\over 2}= {y-4\over -3}= {4-z\over -1} \equiv (2t+3,-3t+4,t+4) 為一直線\\ (D) \bigcirc: 不平行的兩平面交集為一直線 \\(E) \bigcirc: (2-6t,5,-9+8t) 為一直線\\,故選\bbox[red,2pt]{(CDE)}$$
解:$$(B) \times: f'(1)=\lim_{h\to 0} {f(1+h)-f(1) \over h} =\lim_{h\to 0} {|h| \over h} =\pm 1 \Rightarrow f'(1)不存在\\ 其餘導數皆存在,故選\bbox[red,2pt]{(ACDE)}$$公布的答案是(ACE)
解:
$$(A) \bigcirc: \begin{vmatrix}1 & 2 & 3\\ 10 & 20 & 30 \\ 30 & 60 & 90 \end{vmatrix} \xrightarrow{-10r_1+r_2} \begin{vmatrix}1 & 2 & 3\\ 0 & 0 & 0 \\ 30 & 60 & 90 \end{vmatrix}=0 \\(B) \bigcirc: \begin{vmatrix}1 & 2 & 3\\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{vmatrix} \xrightarrow{-4r_1+r_2,-7r_1+r_3} \begin{vmatrix}1 & 2 & 3\\ 0 & -3 & -6 \\ 0 & -6 & -12 \end{vmatrix} \xrightarrow {-2r_2+r_3} \begin{vmatrix}1 & 2 & 3\\ 0 & -3 & -6 \\ 0 & 0 & 0 \end{vmatrix}=0 \\(C)\bigcirc: \begin{vmatrix}1 & 2 & 3\\ 2 & 3 & 4 \\ 3 & 4 & 5 \end{vmatrix} \xrightarrow{-2r_1+r_2,-3r_1+r_3} \begin{vmatrix}1 & 2 & 3\\ 0 & -1 & -2 \\ 0 & -2 & -4 \end{vmatrix} \xrightarrow {-2r_2+r_3} \begin{vmatrix}1 & 2 & 3\\ 0 & -1 & -2 \\ 0 & 0 & 0 \end{vmatrix}=0 \\(D)\times: \begin{vmatrix}1 & 1 & 1\\ 2 & 3 & 4 \\ 2^2 & 3^2 & 4^2 \end{vmatrix} \xrightarrow{-c_1+c_2,-c_1+c_3} \begin{vmatrix}1 & 0 & 0\\ 2 & 1 & 2 \\ 2^2 & 5 & 12 \end{vmatrix} \xrightarrow{-2c_2+c_3} \begin{vmatrix}1 & 0 & 0\\ 2 & 1 & 0 \\ 2^2 & 5 & 2 \end{vmatrix}=2\ne 0\\(E) \bigcirc: \begin{vmatrix}6 & -9 & 3\\ 14 & 20 & -34 \\ -56 & 23 & 33 \end{vmatrix} =6 \begin{vmatrix}2 & -3 & 1\\ 7 &10 & -17 \\ -56 & 23 & 33 \end{vmatrix} \xrightarrow{-2c_3+c_1,3c_3+c_2} 6 \begin{vmatrix}0 & 0 & 1\\ 41 &-41 & -17 \\ -122 & 122 & 33 \end{vmatrix} \\ \qquad \xrightarrow{c_1+c_2} 6 \begin{vmatrix}0 & 0 & 1\\ 41 & 0 & -17 \\ -122 & 0 & 33 \end{vmatrix} =0\\,故選\bbox[red,2pt]{(ABCE)}$$
解:$$f(x)=x^3-3x^2+7 \Rightarrow f'(x)=3x^2-6x \Rightarrow f'(x)\ge 0 \Rightarrow 3x^2-6x \ge 0 \Rightarrow 3x(x-2) \ge 0 \\ \Rightarrow x\ge 2 或x \le 0,故選\bbox[red,2pt]{(ABE)}$$
解:$$(A) \times: \cases{{3\over 2}\pi < \theta < 2\pi \\ \cos \theta={3\over 5}} \Rightarrow \sin \theta =-{4\over 5} \\(B) \times: {3\over 2}\pi < \theta < 2\pi \Rightarrow {3\over 4}\pi < \theta/2 < \pi \Rightarrow \cos {\theta \over 2}< 0 \Rightarrow \cos \theta= \cos (2\cdot {\theta \over 2}) =2\cos ^2{\theta \over 2}-1={3\over 5} \\\qquad \Rightarrow \cos ^2{\theta \over 2}= {4\over 5} \Rightarrow \cos {\theta \over 2} =-{2\over \sqrt 5} \\(C)\bigcirc: \sin \theta = 2\sin{\theta \over 2} \cos {\theta \over 2} = -{4\over 5} \Rightarrow \sin{\theta \over 2}=-{4\over 5}\times {1\over 2}\times (-{\sqrt 5 \over 2}) ={1\over \sqrt 5} \\(D) \bigcirc: \cos 2\theta = 2\cos^2\theta -1=2\times {9\over 25}-1 = -{7\over 25} \\(E) \bigcirc: \sin 2\theta = 2\sin \theta \cos \theta= 2\times (-{4\over 5})\times {3\over 5}= -{24\over 25}\\,故選\bbox[red,2pt]{(CDE)}$$
解:
$$(A)\bigcirc: 面積= 4\times 4\times 2\times {1\over 2}=16 \\(B) \bigcirc: f(x,y)=x+y \Rightarrow \cases{f(A)=-2 \\f(B)=4 \\ f(C)=2 \\ f(D)=-4} \Rightarrow 最大值為4 \\ (C) \bigcirc:g(x,y)=x-y \Rightarrow \cases{g(A)=2 \\ g(B)=4 \\ g(C)=-2 \\ g(D)=-4} \Rightarrow 最小值=-4 \\(D)\bigcirc: h(x,y)=x+3y \Rightarrow \cases{h(A)=-6 \\ h(B)=4 \\ h(C)=6 \\ h(D)=-4} \Rightarrow 最大值=6 \\(E) \bigcirc: p(x,y)=x-3y \Rightarrow \cases{p(A)=6 \\ p(B)=4 \\ p(C)=-6 \\ p(D)=-4} \Rightarrow 最小值=-6\\,故選\bbox[red,2pt]{(ABCDE)}$$
解:$$f(x)=2x^3+6x^2+13 \Rightarrow f'(x)=6x^2+12x \Rightarrow f''(x)=12x+12;\\ f'(x)=0 \Rightarrow 6x^2+12x=0 \Rightarrow 6x(x+2)=0 \Rightarrow x=0,-2 \Rightarrow \cases{f''(0)=12 \ne 0\\ f''(-2)=-12 \ne 0} \\ \Rightarrow x=0,-2有極值,故選\bbox[red,2pt]{(CE)}$$
解:$$(A) \bigcirc:\cases{A_2=\{2,4,6,\dots,60\} \Rightarrow P(A_2)=30/60=1/2 \\A_3=\{3,6,9,\dots, 60\} \Rightarrow P(A_3)=20/60=1/3 \\ A_2\cap A_3= \{6,12,18,\dots,60\} \Rightarrow P(A_2\cap A_3)=10/60=1/6}\\ \Rightarrow P(A_2\cap A_3)=P(A_2)P(A_3) \\(B)\times: \cases{A_7=\{7,14,\dots,56\} \Rightarrow P(A_2)=8/60=2/15 \\A_3\cap A_7= \{21,42\} \Rightarrow P(A_3\cap A_7)=2/60=1/30} \\\Rightarrow P(A_3)P(A_7)=2/45 \ne 1/30 = P(A_3 \cap A_7) \\(C) \bigcirc: A_2\cap A_7=\{ 14,28,42,56\} \Rightarrow P(A_2\cap A_7)=4/60=1/15 = P(A_2)P(A_7) \\(D) \bigcirc: \cases{A_5=\{5,10,\dots,60\} \Rightarrow P(A_5)=12/60=1/5 \\A_2\cap A_3 \cap A_5=\{30,60\} \Rightarrow P(A_2\cap A_3 \cap A_5)=2/60=1/30} \\\qquad \Rightarrow P(A_2)P(A_3)P(A_5)={1\over 2}\times {1\over 3}\times {1\over 5} ={1\over 30} =P(A_2\cap A_3 \cap A_5) \\(E)\times: A_2\cap A_3 \cap A_7= \{42\} \Rightarrow P(A_2\cap A_3 \cap A_7)=1/60 \\\qquad 但 P(A_2)P(A_3)P(A_7) ={1\over 2}\times {1\over 3}\times {2\over 15}={1\over 45}\ne 1/60\\故選\bbox[red, 2pt]{(ACD)}$$
-- END --


















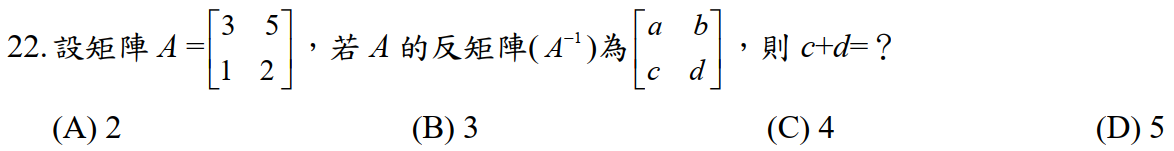




















沒有留言:
張貼留言