高雄區公立高中 109 學年度聯合招考轉學生《高一升高二》
一、單一選擇題
解答:$$\cases{P(三正)=1/8\\ P(二正)=3/8\\ P(一正)=3/8\\ P(三反)=1/8} \quad \Rightarrow 24\times {1\over 8}+16\times {3\over 8} +8\times {3\over 8} =x\times {1\over 8} \Rightarrow x=96,故選\bbox[red, 2pt]{(E)}$$解答:$$\log\left(2-{1\over a}\right) = \log\left(2-{1\over 3}\right) =\log {5\over 3} =\log 5-\log 3= 1-\log 2-\log 3\\ = 1-0.301-0.4771 = 0.2219 \approx 20\%,故選\bbox[red, 2pt]{(B)}$$
解答:$$a_1={6\over 7} \Rightarrow a_2= 2a_1-1 = {5\over 7} \Rightarrow a_3=2a_2-1= {3\over 7} \Rightarrow a_4=2a_3={6\over 7} = a_1\\ \Rightarrow 循環數為3; 由於 2020 = 1 \mod 3,因此a_{2020}= a_1={6\over 7},故選\bbox[red, 2pt]{(E)}$$
解答:$$假設\cases{向正向跳a次\\ 向負向跳b次} \Rightarrow \cases{a+b=10 \\ a-b=-4} \Rightarrow \cases{a=3\\ b=7}\Rightarrow 共有{10!\over 3!7!} =120種跳法,故選\bbox[red, 2pt]{(B)}$$
解答:$$\overline{OP}= \sqrt{41} \Rightarrow x^2+(-5)^2 =41 \Rightarrow x=4 (-4不合,\because P在第四象限) \\\Rightarrow \tan \theta ={-5\over 4},故選\bbox[red, 2pt]{(D)}$$
解答:
$$將選票區分成無交集的區塊,見上圖;依題意\cases{g=174\\ a=b=c=0\\ 665=a+d+f+g \\ 487=b+d+e+g\\ 548 = c+e+f+g } \\ \Rightarrow \cases{ d+f= 491\\ d+e= 313\\ e+f=374} \Rightarrow e=98,故選\bbox[red,2pt]{(C)}$$解答:$$圓心O在x-4y=1上\Rightarrow O=(4t+1,t) \Rightarrow \overline{OA}=\overline{OB} \\\Rightarrow (4t-4)^2+(t+4)^2 = (4t+4)^2+(t-4)^2 \Rightarrow t=0 \Rightarrow O=(1,0) \Rightarrow 半徑r=\overline{OA}\\ =\sqrt{4^2+4^2} =\sqrt{32} \Rightarrow 圓方程式: (x-1)^2 +y^2 = 32,故選\bbox[red,2pt]{(A)}$$
解答:$$令f(x,y)=2x-y-3 \Rightarrow f(P)=-2-3-3 \lt 0 \Rightarrow 若Q與P同側,則f(Q)\lt 0;\\(A)f(3,0)=6 \gt 0\\ (B)f(1,-3)=2+3-3\gt 0\\ (C)f(2,1)=4-1-3=0\\ (D)f(-2,0)=-4-3 \lt 0\\ (E)f(6,5)=12-5-3 \gt 0\\ 故選\bbox[red,2pt]{(D)}$$
解答:
$$\triangle EFC \Rightarrow \overline{EF}=\overline{CF}\sin \alpha = \sin \alpha;\\ 作\overline{FG}\parallel \overline{AB} \Rightarrow \angle AEF = \angle EFG = \angle ECB=\beta \Rightarrow \overline{AF}=\overline{EF} \sin \angle AEF =\sin \alpha \sin \beta\\故選\bbox[red,2pt]{(C)}$$解答:$$依題意:63=31+(95-31)e^{-5k} \Rightarrow e^{-5k} = {1\over 2}\\再經過30分鐘,即總共經過30+5=35分鐘,溫度變為31+(95-31)e^{-35k} =31+64 (e^{-5k})^7 \\= 31+64\cdot ({1\over 2})^7 =31+{1\over 2},故選\bbox[red,2pt]{(E)}$$
解答:$$\cases{\sigma(X)= \sigma(X-1) = \sigma(X+5) = \sigma(-X) \\ \sigma(2X)= 2\sigma(X) \ne \sigma(X)} \Rightarrow 第(1),(2),(4)組資料的標準差相同,故選\bbox[red, 2pt]{(D)}$$
解答:$$觀察所有選項x^3係數,只有(A)是負值,其它選項皆是正值;\\也就是除了(A)之外,圖形都是左下右上,(A)是左上右下;無法藉由平多達成相同圖形\\,故選\bbox[red,2pt]{(A)}$$
解答:$$\cases{a= \sin(-870^\circ) = \sin(-870^\circ+ 360^\circ\times 3) = \sin(210^\circ) = -\sin 30^\circ =-1/2 \\ b=\cos 430^\circ = \cos(430^\circ-360^\circ)= \cos 70^\circ \gt 0\\ c=\tan 1310^\circ = \tan (1310^\circ-360^\circ\times 3) =\tan 230^\circ=\tan 50^\circ \gt 1 } \\ \Rightarrow c\gt b\gt a,故選\bbox[red,2pt]{(E)}$$
解答:$$假設\cases{pH為3的甲溶液有1公升,則其氫離子為10^{-3}莫耳\\pH為7的純水20公升,則其氫離子為20\times 10^{-7}莫耳},\\兩者混合後氫離子濃度變為{10^{-3}+20\times 10^{-7} \over 20+1}= 10^{-7}{10^4+20 \over 21} \approx 500\times 10^{-7} =5\times 10^{-5}\\ \Rightarrow pH值為-\log (5\times 10^{-5} = -(1-\log 2-5)=4.301,故選\bbox[red, 2pt]{(C)}$$
解答:$$\cases{a_1=6 \\a_2=3} \Rightarrow a_3,\dots =\color{blue}{8,4,2,8,6,8},8,4,2,8,6,8,8,4,...,循環數為6;\\ 2009 = 2+ 6\times 334 + 3 \Rightarrow a_{2009} =2,故選\bbox[red,2pt]{(A)}$$
二、多重選擇題
解答:$$(A)\bigcirc: 2x^2+2y^2-3x+y+1=0 \Rightarrow (x-3/4)^2+(y+1/4)^2 =1/8為一圓\\(B) \times: \cases{A(3,-1) \\B(6,2)\\ C(93,89)} \Rightarrow \cases{\overrightarrow{AB} = (3,3)\\ \overrightarrow{BC}=(87,87)} \Rightarrow \overrightarrow{AB} =29\overrightarrow{BC} \Rightarrow 三點在一直線上\\(C)\times: 圓心O(3,-1)至直線4x-3y=5距離={12+3-5\over \sqrt{4^2+3^2}}=2 = 圓半徑\Rightarrow 切點只有一個\\(D)\bigcirc: 圓心(3,-1)至原點距離為\sqrt{10} \Rightarrow 圓至原點距離最長為(\sqrt{10}+\sqrt 7) \gt 5 \Rightarrow P存在\\(E)\bigcirc: 圓心(3,-1)至3x+4y+10=0的距離=3 \gt \sqrt 7 \Rightarrow 圓與直線不相交\\故選\bbox[red,2pt]{(ADE)}$$解答:$$(A)\bigcirc: \sin \angle ACD = \sin(90^\circ +\angle ACB) = \cos \angle ACB=4/5\\(B)\times: \cos \angle DCG = \cos (360^\circ -(180^\circ+\angle ACB))= -\cos \angle ACB = -4/5 \ne -3/5 \\(C)\bigcirc: \triangle ACD ={1\over 2}\overline{CA}\cdot \overline{CD} \sin\angle ACD= {1\over 2} \cdot 4\cdot 5\cdot {4\over 5}=8 \\(D) \times:\triangle CDG ={1\over 2}\overline{CD}\cdot\overline{CG}\cdot\sin \angle DCG ={1\over 2}\cdot 5\cdot 4\cdot {3\over 5}=6\ne 8 \\(E)\bigcirc: \cos \angle DCG = {\overline{CD}^2 + \overline{CG}^2- \overline{DG}^2 \over 2\cdot \overline{CD} \cdot \overline{CG}} \Rightarrow -{4\over 5}={41-\overline{DG}^2 \over 40} \Rightarrow \overline{DG} =\sqrt{73} \\故選\bbox[red,2pt]{(ACE)}$$
解答:$$(A)\times: E(2X+8) =2E(X)+8 = 2\times 4+8=16 \ne 8\\(B)\bigcirc: \sigma_x^2 =Var(X)= E(X^2)-(E(X))^2 \Rightarrow 2^2 = E(X^2)-4^2 \Rightarrow E(X^2)=20\\(C)\times: \sigma(2X+8)= 2\sigma(X) =2\times 2=4 \ne 12 \\(D)\bigcirc: 斜率={\sigma_y\over \sigma_x}r = {3\over 2}\times 0.8={6\over 5}\\(E)\bigcirc: 迴歸直線必過(\mu_x,\mu_y) = (4,6)\\故選\bbox[red,2pt]{(BDE)}$$
解答:$$\cases{a_1,a_2,a_3為等差 \Rightarrow 2a_2=a_1+a_3\\ b_1,b_2,b_3為等比\Rightarrow b_2^2=b_1b_3}\\(A)\bigcirc: (2a_1-3) + (2a_3-3) =2((a_1+a_3)-3) =2(2a_2-3) \\(B)\bigcirc: ({-2\over b_2})^2 = {4\over b_1b_3} ={1\over b_1}\times {4\over b_3}\\ (C)\times: -2,0,2成等差,且-2+0 \lt 0,但0+2 \not \lt 0\\(D)\bigcirc: b_1b_2=b_1^2r \lt 0 \Rightarrow r \lt 0 \Rightarrow b_2b_3=b_2^2r \lt 0\\(E)\times:9,12,16為等比且b_1\lt b_2,但公比r=4/3\not \in \mathbb{N}\\ 故選\bbox[red,2pt]{(ABD)}$$解答:$$(A)\times: f(x)=x^3+1 \Rightarrow \cases{f(-x)=-x^3+1\\ -f(x)=-x^3-1} \Rightarrow f(-x)\ne -f(x) \\(B) \bigcirc: f(x)=-0.01x^3 \Rightarrow \cases{f(-x)= 0.01x^3\\ -f(x)=0.01x^3} \Rightarrow f(-x)=-f(x) \\(C) \bigcirc: f(x)=x(x+1)(x-1) \Rightarrow \cases{f(-x)= -x(x+1)(x-1) \\ -f(x)=-x(x+1)(x-1)} \Rightarrow f(-x)= -f(x)\\ (D)\bigcirc: f(x)= -\sqrt 3x^3+2x \Rightarrow \cases{f(-x)=\sqrt 3x^3-2x\\ -f(x)= \sqrt 3x^3-2x} \Rightarrow f(-x)=-f(x)\\ (E)\times: f(x)=(x-1)^3+2(x-1)+3 \Rightarrow \cases{f(-x)= -(x+1)^3-2(x+1)+3 \\ -f(x)=-(x-1)^3-2(x-1)-3} \Rightarrow f(-x)\ne -f(x)\\故選\bbox[red,2pt]{(BCD)}$$
解答:$$(A)\bigcirc: \triangle ABC ={1\over 2}\overline{AB}\cdot \overline{AC}\sin\angle A={1\over 2}\cdot 8\cdot 4\cdot {1\over 2}=8\\(B)\bigcirc: \cos \angle A={\sqrt 3\over 2}={8^2+\overline{AC}^2-4^2\over 16\overline{AC}} \Rightarrow \overline{AC}= 4\sqrt 3,可求得唯一面積,理由同(A)\\ (C)\times: \cos \angle A={\sqrt 3\over 2}={8^2+\overline{AC}^2-5^2\over 16\overline{AC}} \Rightarrow \overline{AC}= 4\sqrt 3\pm 3 \Rightarrow 有不同的面積\\(D)\times: 同理可求得\overline{AC}=4\sqrt 3\pm 2\sqrt 5 \Rightarrow 有不同的面積\\(E)\bigcirc: 同理可求得\overline{AC}= 8\sqrt 3,可求得唯一面積\\ 故選\bbox[red,2pt]{(ABE)}$$
解答:$$(B)\times: 甲乙丙需排列,共有C^7_3\times 3!種方法\\(D)\times: a^4b^3的係數為-C^7_3\\故選\bbox[red,2pt]{(ACE)}$$
解答:$$\cases{C_1:x^2+y^2=4\\ C_2:x^2+(y+6)^2=4} \Rightarrow \cases{圓心O_1(0,0),半徑r_1=2 \\ 圓心O_2(0,-6),半徑r_2=2}\\(A) \bigcirc: f(x,y) =3x+4y+11 \Rightarrow \cases{f(O_1) f(O_2) \lt 0\\ \text{dist}(O_1,f=0) \gt 2\\ \text{dist}(O_2,f=0) \gt 2} \\(B)\times:f(x,y)=3x+4y-10 \Rightarrow f(O_1)f(O_2) \gt 0\\ (C)\bigcirc:f(x,y)=3x+ 4y+12 \Rightarrow \cases{f(O_1) f(O_2) \lt 0\\ \text{dist}(O_1,f=0) \gt 2\\ \text{dist}(O_2,f=0) \gt 2}\\(D) \bigcirc:f(x,y) = 3x+4y+13 \Rightarrow \cases{f(O_1) f(O_2) \lt 0\\ \text{dist}(O_1,f=0) \gt 2\\ \text{dist}(O_2,f=0) \gt 2}\\(E)\times: f(x,y)=3x+4y+15 \Rightarrow \text{dist}(O_2,f=0) = {9\over 5} \lt 2\\ 故選\bbox[red,2pt]{(ACD)}$$




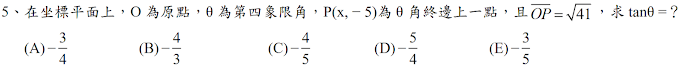




















沒有留言:
張貼留言