109年高雄聯合轉學考-高2升高3-數學詳解

高雄區公立高中109學年度聯合招考轉學生《高2升高3》

一、單選題

解答： $$\begin{vmatrix} 3c-2e & 3d-2f\\ 4a & 4b\end{vmatrix} = -4\begin{vmatrix} a & b&\\3c-2e & 3d-2f \end{vmatrix} = -4\begin{vmatrix} a & b\\3c  & 3d  \end{vmatrix} +4  \begin{vmatrix} a & b\\ 2e &  2f \end{vmatrix} \\= -12\begin{vmatrix} a & b\\c  & d  \end{vmatrix} +8  \begin{vmatrix} a & b\\ e &  f \end{vmatrix}=-12\times 2+ 8\times 5 =-24+40=16，故選\bbox[red,2pt]{(C)}$$

解答： $$\left((x+4)^2 +(y-5)^2+(z+6)^2\right)\left( 3^2 +2^2 +5^2\right) \ge (3(x+4)+ 2(y-5)+5(z+6))^2\\ \Rightarrow \left((x+4)^2 +(y-5)^2+(z+6)^2\right)\times 38 \ge (3x + 2y +5z+32)^2\\ \Rightarrow (x+4)^2 +(y-5)^2+(z+6)^2\ge {(6+32)^2 \over 38} = 38\\ \Rightarrow (x+4)^2 +(y-5)^2+(z+6)^2的最小值為38，故選\bbox[red,2pt]{(D)}$$

解答：

$$\overrightarrow{OP} = a\overline{OA} + b\overrightarrow{OB}，其中-1\le a\le 1,0\le b\le 2 \Rightarrow \overrightarrow{OP} =(5a,0)+(3b,3b) = (5a+3b,3b)\\ 令(x,y) =(5a+3b,3b) \Rightarrow \cases{ -5\le x\le 11\\ 0\le y\le 6 \\ -5\le x-y \le 5} \Rightarrow 所圍區域頂點坐標\cases{A(-5,0)\\ B(5,0)\\ C(11,6)\\ D(1,6)} \\ \Rightarrow 面積=10\times 6=60，故選\bbox[red,2pt]{(A)}$$

解答： $$令B為原點，則\cases{B(0,0,0)\\ C(14,0,0)\\ A(0,0,14)\\ M(7,7,0)\\ N(2,0,0)} \Rightarrow \cases{\overrightarrow{AM} =(7,7,-14) \\ \overrightarrow{AN}= (2,0,-14)} \\\Rightarrow \cos \theta= {\overrightarrow{AM} \cdot \overrightarrow{AN} \over |\overrightarrow{AM}||\overrightarrow{AN}|} ={14+0+14^2\over \sqrt{7^2+7^2+14^2} \times \sqrt{2^2+ 0+14^2}} ={210 \over 7\sqrt 6\times 10\sqrt 2} ={\sqrt 3\over 2} \\ \Rightarrow \theta = 30^\circ，故選\bbox[red,2pt]{(B)}$$

解答： $$\cases{2x-2y+z-3=0\\ xy平面:z=0} \Rightarrow \cases{\vec {n_1}=(2,-2,1)\\ \vec{n_2}=(0,0,1)} \\\Rightarrow \cos \theta = {\vec {n_1} \cdot \vec{n_2} \over |\vec {n_1}||\vec {n_2}|} ={0+0+1\over \sqrt{2^2+2^2+1^2}\cdot \sqrt{0^2+0^2+1^2}} \\ ={1\over 3} \Rightarrow \sin \theta ={2\sqrt 2\over 3}，故選\bbox[red,2pt]{(C)}$$

解答： $$橢圓:{x^2\over 25}+ {y^2\over 5}=1 \Rightarrow \cases{a=5\\ b=\sqrt 5} \Rightarrow c=2\sqrt 5 \Rightarrow 雙曲線\cases{c=2\sqrt 5\\ 2a=6} \Rightarrow \cases{a=3\\ b=\sqrt{11}} \\ \Rightarrow {x^2\over 9}-{y^2\over 11} =1，故選\bbox[red,2pt]{(A)}$$

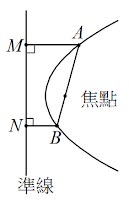
解答：

$$令焦點F，依雙曲線定義可得\cases{\overline{AF} =\overline{AM}=9 \\ \overline{BF} =\overline{BN}=4}；\\作\overline{BC}\bot \overline{AM}(見上圖)，則\overline{BC}^2 = \overline{AB}^2-\overline{AC}^2 =(9+4)^2+(9-4)^2=144 \Rightarrow \overline{BC}=12\\ \Rightarrow \overline{MN}= \overline{BC}=12，故選\bbox[red,2pt]{(B)}$$

解答： $$\cases{E_1:x-2y+2z-5=0\\ E_2:2x+y+z+3=0} \Rightarrow \cases{\vec{n_1}=(1,-2,2)\\ \vec{n_2}=(2,1,1)} \Rightarrow \vec{n_3} = \vec{n_1}\times \vec{n_2} = (-4,3,5)\\ \Rightarrow 過A(1,-1,2)且法向量為\vec{n_3}之平面方程式-4(x-1)+3(y+1) +5(z-2)=0 \\ \Rightarrow -4x+3y+5z-3=0 \Rightarrow 4x-3y-5z=-3，故選\bbox[red,2pt]{(D)}$$

解答：

$$假設\cases{Q是圓心，且半徑為r \\ P為\overline{AB}與\overline{OM}的交點}\qquad，則\cases{\overline{PB}= \overline{OB}\sin 60^\circ= 120\sqrt 3\\ \overline{OP} =\overline{OB}\cos 60^\circ = 120} \\ \Rightarrow \overline{PQ} =\overline{OP}-\overline{OQ} =120-(280-r)=r-160;\\直角\triangle PQB: r^2=(r-160)^2 +(120\sqrt 3)^2 \Rightarrow r=215 \Rightarrow \overline{OQ}=280-215=65\\，故選\bbox[red,2pt]{(E)}$$

解答： $$\tan(\theta-\phi)= {\tan \theta-\tan \phi\over 1+\tan \theta\tan \phi} \Rightarrow {2-\tan \phi\over 1+2\tan \phi} =3 \Rightarrow \tan \phi = -{1\over 7}，故選\bbox[red,2pt]{(D)}$$

解答： $$直線與圓交於A(1,2)及B(2,1)，因此\overline{AB}= \sqrt 2，故選\bbox[red,2pt]{(D)}$$

解答： $$轉換矩陣A=\begin{bmatrix} 0.8 & 0.3 \\ 0.3 & 0.7\end{bmatrix}，趨於穩定後\begin{bmatrix} 甲 \\ 乙\end{bmatrix}= \begin{bmatrix} 0.8 & 0.3 \\ 0.3 & 0.7\end{bmatrix}\begin{bmatrix} 甲 \\ 乙\end{bmatrix} \Rightarrow 2甲=3乙\\ \Rightarrow  \cases{甲占有率=3/5=60\% \\乙占有率=2/5=40\%}，故選\bbox[red,2pt]{(A)}$$

解答： $$\cos 60^\circ = {\vec a\cdot \vec b\over |\vec a||\vec b|} \Rightarrow {1\over 2}={-\sqrt 3k+8 \over \sqrt{64+k^2}\times 2 } \Rightarrow \sqrt{64+k^2} =-\sqrt 3k+8 \\\Rightarrow 64+k^2 = 3k^2-16\sqrt 3k+64 \\ \Rightarrow 2k(k-8\sqrt 3)=0 \Rightarrow k=0或8\sqrt 3，故選\bbox[red,2pt]{(C)}$$

解答： $$8x^2-4\sqrt 3x+1=0 的兩根為{\sqrt 3\pm 1\over 4} \Rightarrow \sin A={\sqrt 3-1\over 4} \Rightarrow {\overline{BC} \over \sin A} =2R \\\Rightarrow R= {2\over \sqrt 3-1} =\sqrt 3+1，故選\bbox[red,2pt]{(E)}$$

解答： $$\cases{\vec a=(2,1,2) \\ \vec b=(x,y,z)} \Rightarrow \vec a\cdot \vec b=2x+y+2z \Rightarrow (x^2+y^2 +z^2)(2^2 + 1^2 +2^2) \ge (2x+y+2z)^2\\ \Rightarrow |\vec b|^2\times 9 \ge \vec (a\cdot \vec b)^2 \Rightarrow \vec a\cdot \vec b \le \sqrt{9^2\times 9} = 27，故選\bbox[red,2pt]{(D)}$$

二、多選題

解答： $$\cases{\vec u,\vec v均為單位向量\Rightarrow |\vec u|=|\vec v|=1\\ \vec u\bot \vec v \Rightarrow \vec u\cdot \vec v=0}\\(A)\bigcirc:  \cases{|\vec u+\vec v|^2=(\vec u+\vec v)\cdot (\vec u+\vec v)= |\vec u|^2 +2\vec u\cdot \vec v+|\vec v|^2=2\\ |\vec u-\vec v|^2=(\vec u-\vec v)\cdot (\vec u-\vec v)= |\vec u|^2 -2\vec u\cdot \vec v+|\vec v|^2=2}  \Rightarrow |\vec u+\vec v|=|\vec u-\vec v|\\(B) \bigcirc:(\vec u+\vec v)\cdot (\vec u-\vec v) = |\vec u|^2-\vec u\cdot \vec v+\vec v\cdot \vec u-|\vec v|^2=0 \Rightarrow (\vec u+\vec v) \bot (\vec u-\vec v) \\(C) \times:\cases{\cos 135^\circ =-1/\sqrt 2\\ {(\vec u+\vec v)\cdot \vec v\over |\vec u+\vec v||\vec v|} ={1\over |\vec u+\vec v|} 不可能負值} \qquad \Rightarrow 夾角\theta不可能為135^\circ \\(D)\bigcirc: |a\vec u+b\vec v|^2 = (a\vec u+b\vec v)\cdot (a\vec u+b \vec v) =a^2+b^2 \Rightarrow |a\vec u+b\vec v|=\sqrt{a^2+b^2}\\(E)\times: {(\vec u-\vec v)\cdot \vec v\over |\vec u-\vec v||\vec v|} ={-|\vec v|^2\over |\vec u-\vec v|} ={-1\over \sqrt 2} \Rightarrow (\vec u-\vec v)與\vec v的夾角不是45^\circ\\ 故選\bbox[red,2pt]{(ABD)}$$

解答： $$\cases{270^\circ \lt \theta \lt 360^\circ \\ \cos \theta=1/3} \Rightarrow \sin \theta = -{2\sqrt 2\over 3} \Rightarrow \cases{\sin(2\theta)= 2\sin \theta \cos \theta= -4\sqrt 2/9 \\ \cos(2\theta)= \cos^2\theta-\sin^2\theta =-7/9} \\ \Rightarrow \tan (2\theta)= {\sin (2\theta)\over \cos(2\theta)} ={4\sqrt 2\over 7}，故選\bbox[red,2pt]{(ADE)}$$

解答： $$(A)\times: x^2+y^2+2x-10y+30=0 \Rightarrow (x+1)^2 +(y-5)^2+4=0非圓方程式\\(B)\times: A,B,C皆在同一直線:y=9x-12，無法同時在一圓上\\(C)\times: 圓心(2,-3)至直線3x-4y+7=0的距離={25\over 5}=5=半徑\Rightarrow 相切，因此有2個切點 \\(D)\bigcirc:圓心(2,-3)與直線3x-4y-13=0的距離=1 \Rightarrow 半徑\sqrt 5-1 < 2 \\\qquad \Rightarrow 僅有一側圓弧上的兩點與直線距離為2，另一側皆小於2\\ (E) \bigcirc:\sqrt{a^2+b^2}相當於圓上的點至原點的距離，\\\qquad 而\cases{圓至原點最長的距離為圓心至原點距離加上半徑=d_1=2+\sqrt{13} \\圓至原點最短的距離為圓心至原點距離減去半徑=d_2=\sqrt{13}-2}\\ \Rightarrow \cases{ d_1\lt 6\\ 1\lt d_2  } \Rightarrow 介於d_1與d_2之間的整數為2,3,4,5，共有4個\Rightarrow 兩側共有8個點與原點距離為整數\\故選\bbox[red,2pt]{(DE)}$$

解答： $$(A)\bigcirc: 方向向量為(1,2,-3) \Rightarrow (-1,-2,3)亦為方向向量\\(B)\bigcirc: (1,2,-3)為L與L_1交點，且兩直線有不同的方向向量\\(C)\times: \cases{P在L:{x-1\over 1} ={y-2\over 2} ={z+3 \over -3} \\ Q在L_2:{x\over 1} ={y\over 1} ={z \over -1} } \Rightarrow \cases{P(t+1,2t+2,-3t-3)\\ Q(s,s,-s)}\\\qquad \Rightarrow 當\cases{t=-1\\ s=0}時，P=Q=(0,0,0) \Rightarrow 兩直線有交點，非歪斜\\(D)\times: L與L_3有相同的方向量，且(1,2,-3)為其交點，因此兩直線重疊，非平行\\(E)\bigcirc: L與L_4有相同方向向量，且無交點，故平行\\ 故選\bbox[red,2pt]{(ABE)}$$

解答： $$\cases{抽到奇號球的機率為3/5\\ 抽到偶號球的機率為2/5} \Rightarrow \cases{p_{n+1}= {2\over 5}p_{n} +{3\over 5}q_{n} \\q_{n+1} ={3\over 5}p_n+ {2\over 5}p_{n }} \Rightarrow \begin{bmatrix} p_{n+1}\\ q_{n+1}\end{bmatrix} =\begin{bmatrix} 2/5 & 3/5\\ 3/5& 2/5 \end{bmatrix}\begin{bmatrix} p_{n}\\ q_{n}\end{bmatrix}\\(A)\bigcirc: 不是奇數就是偶數，因此p_n+q_n=1\\ (B)\times:\begin{bmatrix} p_{2}\\ q_{2}\end{bmatrix} =\begin{bmatrix} 2/5 & 3/5\\ 3/5& 2/5 \end{bmatrix}\begin{bmatrix} p_{1}\\ q_{1}\end{bmatrix} =\begin{bmatrix} 2/5 & 3/5\\ 3/5& 2/5 \end{bmatrix}\begin{bmatrix} 3/5\\ 2/5\end{bmatrix} = \begin{bmatrix} 12/25\\ 13/25\end{bmatrix} \Rightarrow p_2=12/25 < 1/2 \\(C)\bigcirc:\begin{bmatrix} p_{3}\\ q_{3}\end{bmatrix} =\begin{bmatrix} 2/5 & 3/5\\ 3/5& 2/5 \end{bmatrix}\begin{bmatrix} p_{2}\\ q_{2}\end{bmatrix} =\begin{bmatrix} 2/5 & 3/5\\ 3/5& 2/5 \end{bmatrix}\begin{bmatrix} 12/25\\ 13/25\end{bmatrix} =\begin{bmatrix} 63/125\\ 62/125\end{bmatrix}\Rightarrow p_3=63/125 \gt 1/2\\(D) \bigcirc:\cases{a=d=2/5\\ b=c=3/5} \\(E)\times: p_{n+1}={2\over 5}p_n+ {3\over 5}q_n ={2\over 5}p_n+ {3\over 5}(1-p_n) = {3\over 5}-{1\over 5}p_n\\故選\bbox[red,2pt]{(ACD)}$$

解答： $$(A)\times: \overline{BC}邊上的高=\overline{AB}\sin \angle B=c\sin B\\ 其餘皆正確，故選\bbox[red,2pt]{(BCDE)}$$

解答： $$P在y^2=4x 上\Rightarrow P({t^2\over 4},t) \Rightarrow f(t)=\text{dist}(P,y=x+5) = {{t^2\over 4}-t+5\over \sqrt 2} ={1\over \sqrt 2}({1\over 4}(t^2-4t+4)+4)\\ ={1\over \sqrt 2}({1\over 4}(t-2)^2+4) \Rightarrow 當t=2時，f(2)=2\sqrt 2為最小值，此時P=(1,2)；\\過P且斜率為-1之直線: y=-(x-1)+2與直線y=x+5相交於Q(-1,4)；\\因此\cases{P(1,2)\\ Q(-1,4)\\ m=2\sqrt 2}，故選\bbox[red, 2pt]{(ACD)}$$

解答： $$\cases{P(x,4)\\ \cos \theta=3/5} \Rightarrow \cases{x=3 \\ \overline{OP}=5}\Rightarrow \sin \theta =4/5 \Rightarrow \tan \theta= 4/3 \Rightarrow \sin 2\theta = 2\sin\theta \cos \theta = {24\over 25} \gt 0 \\，故選\bbox[red,2pt]{(CD)}$$