104年臺北市松山家商教甄-數學詳解

臺北市立松山家商104學年度第 1 次教師甄選初試

第壹部分：填充題(佔64分)

解答：

$$令\cases{\overline{AC}=a\\ \angle C=\theta} \Rightarrow \angle A=2\theta \Rightarrow \cases{\cos \angle A={4+a^2-9\over 4a} \\ \cos \angle C={9+a^2-4\over 6a}} \Rightarrow \cases{\cos 2\theta ={a^2-5\over 4a} \\\cos \theta ={a^2+5\over 6a}} \\ \cos 2\theta =2\cos^2\theta -1 \Rightarrow {a^2-5\over 4a}=2 \left( {a^2+5\over 6a}\right)^2-1 \Rightarrow {a^2+4a-5 \over 4a} ={a^4+10a^2+25\over 18a^2} \\ \Rightarrow 9a^3+36a^2-45a=2a^4+20a^2+50 \Rightarrow 2a^4-9a^3-16a^2+45a+50=0\\ \Rightarrow (a+1)(2a^3-11a^2-5a+50)=0 \Rightarrow (a+1)(a+2)(2a^2-15a+25)=0 \\ \Rightarrow (a+1)(a+2)(2a-5)(a-5)=0 \Rightarrow a= \bbox[red,2pt]{5\over 2}(5不合，違反\triangle 二邊和大於第三邊)$$

解答： $$令\log_4 m=\log_6 n =\log_9 (m+n)=a \Rightarrow \cases{m=4^a\\ n=6^a\\ m+n=9^a} \Rightarrow \cases{m/n= ({ 4\over 6})^a = ({2\over 3})^a \cdots(1)\\4^a+6^a=9^a \Rightarrow ({4\over 9})^a+ ({6\over 9})^a =1\cdots(2)} \\ 將(1)代入(2) \Rightarrow ({m\over n})^2+{m\over n}-1=0 \Rightarrow {m\over n}={-1+\sqrt{5}\over 2} \Rightarrow {n\over m}={2\over \sqrt 5-1} =\bbox[red,2pt]{\sqrt 5+1\over 2}$$

解答： $$x\gt 1或x\lt -2 \Rightarrow (x-1)(x+2) \gt 0，\\因此若(x+2)(x-1)(x^2-mx+m) \gt 0 \Rightarrow x^2-mx+m \gt 0\\ \Rightarrow 判別式\;m^2-4m \lt 0 \Rightarrow m(m-4)\lt 0\Rightarrow 0\lt m\lt 4\\ 又m=0時,x^2-mx+m= x^2 \gt 0(\because x\ge 1或x\lt -2) \Rightarrow \bbox[red,2pt]{0\le m\lt 4}$$

解答：

$$E、F在\overline{BC}上，且\overline{AE}\bot \overline{BC}及\overline{DF}\bot \overline{BC} \Rightarrow \overline{CF}=(\overline{BC}-\overline{AD})\div 2 =(10-6)\div 2=2\\ 直角\triangle DFC \Rightarrow \overline{DF}=\sqrt{5^2-2^2} =\sqrt{21}；又直角\triangle DFB \Rightarrow \overline{DB}=\sqrt{21+8^2} =\sqrt{85}\\ \Rightarrow \cos \angle ADB = {36+85- 25\over 12 \sqrt{85}} ={8\over \sqrt{85}} \\\Rightarrow \overrightarrow{DA} \cdot  \overrightarrow{DB} =\overline{DA}\times \overline{DB}\times \cos\angle ADB =6 \sqrt{85}\times {8\over \sqrt{85}}  =\bbox[red, 2pt]{48}$$

解答：

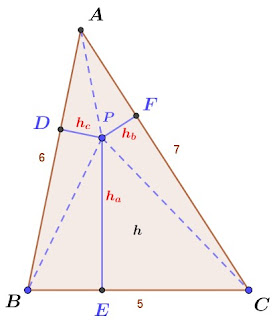
$$令\cases{a=\overline{BC}=5 \\ b=\overline{AC}=7\\ c=\overline{AB}=6} 及\cases{h_c=\overline{PD} \\h_a=\overline{PE} \\h_b=\overline{PF} }及\overline{BC}上的高為h，見上圖；\\令s=(a+b+c)\div 2=9 \Rightarrow \cases{\triangle ABC面積=\sqrt{ s(s-a)(s-b)(s-c)} =\sqrt{9\cdot 4\cdot 2\cdot 3} =6\sqrt 6\\ \triangle ABC面積={1\over 2}(5h_a+ 7h_b+6h_c)} \\ \Rightarrow 5h_a+ 7h_b+6h_c=12\sqrt 6；又5h_a+ 7h_b+6h_c \le 7h_a+ 7h_b+7h_c=7(h_a+h_b+h_c) \\ \Rightarrow h_a+h_b+h_c \ge \bbox[red,2pt]{12\sqrt 6\over 7}$$

解答： $$x^2-px-q=0 的正根x={p+\sqrt{p^2+4a}\over 2} \lt 3 \Rightarrow \sqrt{p^2+4q} \lt 6-p \Rightarrow p^2+4q \lt (p-6)^2\\ \Rightarrow 12p+4q \lt 36 \Rightarrow (p,q)=(1,1-5),(2,1-2)，共有5+2=\bbox[red, 2pt]{7}組解$$

解答： $$令\cases{A:黑球比紅球先取完\\ B:黑球比白球先取完}\quad\qquad，則欲求之P(A\cap B)= P(A)+P(B)-P(A\cup B)\\ \cases{6紅4黑排列數:{10!\over 4!6!}\\5紅4黑排列數:{9!\over 5!4!}}\qquad；若最後一球是紅球就代表黑球比紅球先取完，機率為{{9!\over 5!4!} \over {10!\over 4!6!}} ={6\over 10}\\，即P(A)={6\over 10}; 同理P(B)={5\over 9}，P(A\cup B)={11\over 15}；因此P(A\cap B)={6\over 10} +{5\over 9}-{11\over 15} = \bbox[red,2pt]{19\over 45}$$

解答： $$六次投擲的結果為a_1b_1a_2b_2a_3b_3，其中\cases{a_i,b_i\in \{0=反面,1=正面\}\\a_i代表甲第i次投擲的結果 \\b_i代表乙第i次投擲的結果}\\擲完第3次甲領先的情形:a_1b_1a_2=101,111,100,001；\\每一種情形的後3次投擲有2^3=8種情形，共8\times 4=32種；\\僅考量後3次的結果，有4種是甲\ge 乙(000,010,011,110)，另4種是乙\gt 甲(001,100,101,111)；\\a_1b_1a_2=101後8種情形中，只有101無法達成甲最後領先，即7種符合要求；\\a_1b_1a_2=111,100,001後8種情形中，取4種甲\ge 乙即符合要求，即共有3\times 4=12種\\ 因此機率為{7+12\over 32} =\bbox[red,2pt]{19\over 32}$$

第貳部份:計算證明題

解答：

(1)

$$聯立不等式:\cases{8x+9y\le 240\\ 2x+y\le 50\\ x+3y\le 60\\ 0\le x,y}，圖形如上；$$ (2) $$利潤f(x,y)=7x+5y \Rightarrow \cases{f(0,20)=100\\ f(12,16)=164\\ f(21,8)=187 \\f(25,0)=175} \Rightarrow 生產\bbox[red,2pt]{\cases{A產品21噸\quad \\ B產品8噸}}\quad可獲得最高利潤\bbox[red,2pt]{187萬元}$$

解答：

(1) $$\overrightarrow{OP}= \overrightarrow{OA} +\overrightarrow{AP} = \overrightarrow{OA} +{5\over 7}\overrightarrow{AB} = \overrightarrow{OA} +{5\over 7}(-\overrightarrow{OA}+\overrightarrow{OB}) ={2\over 7}\overrightarrow{OB} +{5\over 7}\overrightarrow{OB}，\bbox[red,2pt]{故得證}$$ (2) $$令\overline{AB}中點為D \Rightarrow \overline{OG}={2\over 3}\overline{OD}\\  又 \cases{\triangle OPG: \triangle OAD=\overline{OP}\times \overline{OG}: \overline{OA}\times \overline{OD} =h\overline{OA}\times {2\over 3}\overline{OD}: \overline{OA}\times \overline{OD} ={2h\over 3}:1 \\ \triangle OQG:\triangle ODB =\overline{OG}\times \overline{OQ}: \overline{OD} \times \overline{OB} ={2\over 3}\overline{OD}\times k\overline{OB}: \overline{OD} \times \overline{OB}={2k\over 3}:1}\\ 由於\triangle OAD=\triangle ODB ={1\over 2}\triangle OAB \Rightarrow \cases{\triangle OPG={2h\over 3}\triangle OAD ={h\over 3}\triangle OAB\\ \triangle OQG={2k\over 3}\triangle ODB ={k\over 3}\triangle OAB} \\ \Rightarrow {\triangle OPQ \over \triangle OAB} ={\triangle OPG +\triangle OQG\over \triangle OAB} ={(h/3+k/3)\triangle OAB \over \triangle OAB} ={h+k\over 3}={9\over 20} \Rightarrow h+k=\bbox[red,2pt]{27\over 20}$$

解答：

$$假設\overline{CD}=a(0\lt a\lt 7)，則 新路線費用:7-a+\sqrt{a^2+25}\times n\\ f(a)=7-a+\sqrt{a^2+25}\times n \Rightarrow f'(a)=0 \Rightarrow -1+{na\over \sqrt{a^2+25}}=0 \Rightarrow a=\bbox[red,2pt]{5\over \sqrt{n^2-1}}$$

======================= END =========================

解題僅供參考，學校未公布計算證明題的答案，其它教甄試題及詳解