教育部105年專科學校畢業程度自學進修學力鑑定考試
專業科目(一): 初級統計
解答:$$顯著水準也就是型I錯誤,拒絕正確的虛無假設,故選\bbox[red,2pt]{(C)}$$
解答:$$A、B獨立\Rightarrow P(A\cap B)=P(A)\cdot P(B) \Rightarrow P(B\mid A)= {P(B \cap A)\over P(A)} ={P(B)P(A)\over P(A)}\\ =P(B)=0.3,故選\bbox[red,2pt]{(B)}$$
解答:$$信賴區間上限= p+z_{\alpha/2}\sqrt{p(1-p)\over n} =0.3+1.96\times \sqrt{0.3\times 0.7\over 100} =0.389,故選\bbox[red,2pt]{(C)}$$
解答:$$\begin{array}{c|cc}&正面 &反面\\\hline 觀察值& 70& 30\\ 期望值& 50 & 50 \end{array} \Rightarrow \chi^2 ={(70-50)^2\over 50}+ {(30-50)^2\over 50}=16,故選\bbox[red,2pt]{(C)}$$
解答:$$X\sim B(4,1/2) \Rightarrow EX=np= 4\times {1\over 2}=2,故選\bbox[red,2pt]{(B)}$$
解答:$$\begin{array}{} & X & Y & X^2& XY & Y^2 \\\hline & 2 & 3 & 4& 6 & 9\\ &3 & 2 & 9 & 6 & 4 \\ &5 & 6& 25 & 30 & 36 \\\hline \sum & 10 & 11 & 38 & 42 & 49\end{array}\\ 斜率b_1 = {\sum XY - \sum X\sum Y/n\over \sum X^2-(\sum X)^2/n} ={42-110/3 \over 38-100/3} =1.1429,故選\bbox[red,2pt]{(D)}$$
解答:$$\cases{\bar x=\sum X/n =10/3\\ \bar y=\sum Y/n = 11/3} \Rightarrow 回歸直線L:y=b_1(x-\bar x)+\bar y =1.143(x-10/3)+11/3\\ \Rightarrow y= 1.143x-0.143 \Rightarrow 截距=-0.143,故選\bbox[red,2pt]{(B)}$$
解答:$$x=4代入迴歸直線 \Rightarrow y=1.143\times 4-0.143=4.429,故選\bbox[red,2pt]{(C)}$$
解答:$$相關係數r={\sum XY - \sum X\sum Y/n\over \sqrt{\sum X^2-(\sum X)^2/n} \cdot \sqrt{\sum Y^2-(\sum Y)^2/n}} ={42-110/3 \over \sqrt{38-100/3} \cdot \sqrt{49-121/3}}\\= 0.839,故選\bbox[red,2pt]{(A)}$$
解答:$$R^2= r^2=0.839^2= 0.703,故選\bbox[red,2pt]{(B)}$$
解答:$$依估計式特性定義,只有(D)不正確,故選\bbox[red,2pt]{(D)}$$
解答:$$(A)應是母體統計量落入區間的機率,故選\bbox[red,2pt]{(A)}$$
解答:$$P(A\cup B)= P(A)+P(B)-P(A\cap B) \Rightarrow 0.6=P(A)+0.4-0.2 \Rightarrow P(A)=0.4,故選\bbox[red,2pt]{(C)}$$
解答:$$X\sim B(n=3,p=0.4) \Rightarrow P(X\ge 1)=1-P(X=0) = 1-(1-0.4)^3= 0.784,故選\bbox[red,2pt]{(B)}$$
解答:$$X\sim Po(\lambda=15,T=2) \Rightarrow P(X=k)= (\lambda T)^k\cdot {e^{-\lambda T}\over k!} \Rightarrow P(X=1,\lambda=15,T=2)=30\cdot e^{-30}\\,故選\bbox[red,2pt]{(D)}$$
解答:$$\sum P=1 \Rightarrow P(X=1)+P(X=2) +P(X=3)=k+2k+3k=6k= 1\Rightarrow k={1\over 6},故選\bbox[red,2pt]{(A)}$$
解答:$${3\over 10} \times {3\over 10}={9\over 100},故選\bbox[red,2pt]{(A)}$$
解答:$$E(Y)= E(X+2)= E(X)+2 = 100\times 0.05+2 =7,故選\bbox[red,2pt]{(C)}$$
解答:$$X\sim Po(\lambda=2) \Rightarrow Var(X)=\lambda =2,故選\bbox[red,2pt]{(B)}$$
解答:$$C^5_1C^5_1/C^{10}_2 ={5\over 9},故選\bbox[red,2pt]{(D)}$$
解答:$$依序為6,7,8 \Rightarrow 中位數=7,故選\bbox[red,2pt]{(B)}$$
解答:$$0.2^3=0.008,故選\bbox[red,2pt]{(A)}$$
解答:$$\bbox[blue,2pt]{題目有誤}應該是A:第1次擲出偶數點事件 \Rightarrow A=\{(2,1-6),(4,1-6),(6,1-6)\},共有18種;\\A\cap B=\{(2,3),(4,3),(6,3)\},共有3種;因此P(B\mid A)={P(B\cap A)\over P(A)}=3/18=1/6,故選\bbox[red,2pt]{(B)}$$
解答:$$\bar x=(1+2+3+4+5) \div 5=3 \Rightarrow s^2= {2^2+1^2+0^2+1^2+2^2 \over 5-1} ={10\over 4}=2.5,故選\bbox[red,2pt]{(C)}$$
解答:$$\bar x-z_{\alpha/2}{s\over \sqrt n} =82-2.575\times {4\over \sqrt{49}} = 80.53,故選\bbox[red,2pt]{(D)}$$
解答:$$X\sim B(n=3,p=1/2) \Rightarrow P(X=2)=C^3_2p^2(1-p) =3\times ({1\over 2})^3= {3\over 8},故選\bbox[red,2pt]{(C)}$$
解答:$$擲骰子出現奇數的機率為{3\over 6}={1\over 2} \Rightarrow 兩次都奇數的機率=({1\over 2})^2={1\over 4},故選\bbox[red,2pt]{(C)}$$
解答:$$E= z_{\alpha/2}\cdot \sqrt{p(1-p)\over n} =1.645\times \sqrt{(1/4)\cdot (3/4)\over 120} =0.065=6.5\%,故選\bbox[red,2pt]{(A)}$$
解答:
$$\cases{銀行有5家\Rightarrow df_B=5-1=4\\ 樣本數n=6+5+6+7+6=30 } \Rightarrow df_W=n-1-df_B=25 \\\Rightarrow MSE=60/df_W=60/25= 2.4 \Rightarrow F=42/MSE = 42/2.4=17.5,故選\bbox[red,2pt]{(A)}$$
解答:$$0.6\times 0.02+0.4\times 0.03 =0.012+0.012=0.024,故選\bbox[red,2pt]{(B)}$$
解答:$$P(\hat P<0.1) \Rightarrow P(Z \lt {0.1-0.07\over \sqrt{0.1\times 0.9/100}})= P(Z\lt 1) \\\Rightarrow P值=1-P(Z\lt 1)= P(Z\gt 1)=0.16,故選\bbox[red,2pt]{(C)}$$
解答:$$信賴區間長度=2t_{\alpha/2}(n-1){s\over \sqrt n} =2t_{0.05}(8){2.4\over \sqrt 9} =2\times 1.86\times 0.8= 2.976,故選\bbox[red,2pt]{(A)}$$
解答:$$\cases{p_1=4/5,n_1=50\\ p_2=3/5,n_2=50} \Rightarrow S_{p_1-p_2}=\sqrt{{p_1(1-p_1)\over n_1} +{p_2(1-p_2)\over n_2}}\\ =\sqrt{{(4/5)\cdot (1/5)\over 50} +{(3/5)\cdot (2/5)\over 50}} ={\sqrt 5\over 25} \Rightarrow {p_1-p_2\over S_{p_1-p_2}} ={0.2\over \sqrt 5/25}=\sqrt 5 =2.236\\,選項中只能挑最接近的,故選\bbox[red,2pt]{(D)}$$
解答:$$V(Y)=V(2X)= 4V(X)=4\times np(1-p)=4\times 1\cdot {1\over 2}\cdot {1\over 2}=1,故選\bbox[red,2pt]{(D)}$$
解答:$$ 良品機率=P(8\le X\le 12)= P({8-10\over 2} \le Z \le {12-10\over 2}) = P(-1\le Z\le 1)\\ \Rightarrow 不良品機率= P(Z\lt -1)+P(Z\gt 1)= 2P(Z\lt -1)=2\times 0.1587=0.3174,故選\bbox[red,2pt]{(B)}$$
解答:$$E(X_1-X_2)=E(X_1)-E(X_2)=E(X)-E(X)=0,故選\bbox[red,2pt]{(A)}$$
解答:$$X\sim N(20,4^2) \Rightarrow \bar x \to \mu=20,故選\bbox[red,2pt]{(C)}$$
解答:$$V(Y)=V(5X-1)= 25V(X)=25\times 1=25,故選\bbox[red,2pt]{(D)}$$
解答:$$V(T)=V(X-Y) =V(X)+V(Y)= 4+2=6,故選\bbox[red,2pt]{(C)}$$
解答:$$n={(z_{\alpha/2})^2s^2\over E^2}= {1.645^2 \times 2.4^2 \over 0.5^2} =62.35,故選\bbox[red,2pt]{(B)}$$
解答:$$V({2x_1+x_2+x_3+2x_4\over 6})={1\over 36}(4V(x_1)+V(x_2)+V(x_3)+4V(x_4))= {10\over 36}V(X)= {\sqrt{10}\over 6}\sigma = c\sigma\\ \Rightarrow c={\sqrt{10}\over 6} =0.527,故選\bbox[red,2pt]{(A)}$$
解答:$$n_1E_1^2 = n_2E_2^2 \Rightarrow 80\times 0.03^2 = n_2\times 0.02^2 \Rightarrow n_2=180,故選\bbox[red,2pt]{(D)}$$
解答:$${75-72\over 8/\sqrt n}=2.56 \Rightarrow n=46.6,故選\bbox[red,2pt]{(A)}$$
解答:$$n= (z_{\alpha/2})^2 \cdot {p(1-p)\over E^2} =1.96^2 \times {0.3\times 0.7\over 0.05^2} =322.69,故選\bbox[red,2pt]{(C)}$$
解答:$$\bar x=(1.01+ 1.01+0.96 +1.02)\div 4=1 \\\Rightarrow s^2 =(0.01^2+0.01^2+0.04^2+0.02^2)\div 3={11\over 5000}\times {1\over 3}\\ 標準差下限值= \sqrt{(n-1)s^2\over \chi^2_{\alpha/2}(n-1)} = \sqrt{11/5000\over 7.82} = 0.0168,故選\bbox[red,2pt]{(D)}$$
解答:$$n_1E_1^2 = n_2E_2^2 \Rightarrow 50\times 2^2=n_2\times 1.5^2 \Rightarrow n_2= 88.89,故選\bbox[red,2pt]{(A)}$$
解答:$${n_1 \over (z_{\alpha_1/2})^2} = {n_2 \over (z_{\alpha_2/2})^2} \Rightarrow {175 \over 1.96^2} ={n_2 \over 1.645^2} \Rightarrow n_2= 123.27,故選\bbox[red,2pt]{(C)}$$
解答:$$顯著水準=0.05,經查表P(Z\gt 1.645)=0.05 \Rightarrow 臨界值=100+1.645=101.645\\,而現在為103,與臨界值相差103-101.645=1.355 \Rightarrow P(Z\gt 1.355)\approx 0.09,故選\bbox[red,2pt]{(B)}$$
解答:$$依柴比雪夫不等式:P(|X-\mu|\ge b) \le {\sigma^2 \over b^2} \Rightarrow P(|X-70|\ge 10) \le {5^2 \over 10^2}=25\%\\ 因此P(60\le X\le 80)= P( |X-70|\le 10) = 1- P(|X-70|\ge 10)=1-25\% = 75\%\\ \Rightarrow 600\times 75\% =450,故選\bbox[red,2pt]{(D)}$$
======================= END =====================
解答:$$0.6\times 0.02+0.4\times 0.03 =0.012+0.012=0.024,故選\bbox[red,2pt]{(B)}$$
解答:$$P(\hat P<0.1) \Rightarrow P(Z \lt {0.1-0.07\over \sqrt{0.1\times 0.9/100}})= P(Z\lt 1) \\\Rightarrow P值=1-P(Z\lt 1)= P(Z\gt 1)=0.16,故選\bbox[red,2pt]{(C)}$$
解答:$$信賴區間長度=2t_{\alpha/2}(n-1){s\over \sqrt n} =2t_{0.05}(8){2.4\over \sqrt 9} =2\times 1.86\times 0.8= 2.976,故選\bbox[red,2pt]{(A)}$$
解答:$$\cases{p_1=4/5,n_1=50\\ p_2=3/5,n_2=50} \Rightarrow S_{p_1-p_2}=\sqrt{{p_1(1-p_1)\over n_1} +{p_2(1-p_2)\over n_2}}\\ =\sqrt{{(4/5)\cdot (1/5)\over 50} +{(3/5)\cdot (2/5)\over 50}} ={\sqrt 5\over 25} \Rightarrow {p_1-p_2\over S_{p_1-p_2}} ={0.2\over \sqrt 5/25}=\sqrt 5 =2.236\\,選項中只能挑最接近的,故選\bbox[red,2pt]{(D)}$$
解答:$$V(Y)=V(2X)= 4V(X)=4\times np(1-p)=4\times 1\cdot {1\over 2}\cdot {1\over 2}=1,故選\bbox[red,2pt]{(D)}$$
解答:$$ 良品機率=P(8\le X\le 12)= P({8-10\over 2} \le Z \le {12-10\over 2}) = P(-1\le Z\le 1)\\ \Rightarrow 不良品機率= P(Z\lt -1)+P(Z\gt 1)= 2P(Z\lt -1)=2\times 0.1587=0.3174,故選\bbox[red,2pt]{(B)}$$
解答:$$E(X_1-X_2)=E(X_1)-E(X_2)=E(X)-E(X)=0,故選\bbox[red,2pt]{(A)}$$
解答:$$X\sim N(20,4^2) \Rightarrow \bar x \to \mu=20,故選\bbox[red,2pt]{(C)}$$
解答:$$V(Y)=V(5X-1)= 25V(X)=25\times 1=25,故選\bbox[red,2pt]{(D)}$$
解答:$$V(T)=V(X-Y) =V(X)+V(Y)= 4+2=6,故選\bbox[red,2pt]{(C)}$$
解答:$$n={(z_{\alpha/2})^2s^2\over E^2}= {1.645^2 \times 2.4^2 \over 0.5^2} =62.35,故選\bbox[red,2pt]{(B)}$$
解答:$$V({2x_1+x_2+x_3+2x_4\over 6})={1\over 36}(4V(x_1)+V(x_2)+V(x_3)+4V(x_4))= {10\over 36}V(X)= {\sqrt{10}\over 6}\sigma = c\sigma\\ \Rightarrow c={\sqrt{10}\over 6} =0.527,故選\bbox[red,2pt]{(A)}$$
解答:$$n_1E_1^2 = n_2E_2^2 \Rightarrow 80\times 0.03^2 = n_2\times 0.02^2 \Rightarrow n_2=180,故選\bbox[red,2pt]{(D)}$$
解答:$${75-72\over 8/\sqrt n}=2.56 \Rightarrow n=46.6,故選\bbox[red,2pt]{(A)}$$
解答:$$n= (z_{\alpha/2})^2 \cdot {p(1-p)\over E^2} =1.96^2 \times {0.3\times 0.7\over 0.05^2} =322.69,故選\bbox[red,2pt]{(C)}$$
解答:$$\bar x=(1.01+ 1.01+0.96 +1.02)\div 4=1 \\\Rightarrow s^2 =(0.01^2+0.01^2+0.04^2+0.02^2)\div 3={11\over 5000}\times {1\over 3}\\ 標準差下限值= \sqrt{(n-1)s^2\over \chi^2_{\alpha/2}(n-1)} = \sqrt{11/5000\over 7.82} = 0.0168,故選\bbox[red,2pt]{(D)}$$
解答:$$n_1E_1^2 = n_2E_2^2 \Rightarrow 50\times 2^2=n_2\times 1.5^2 \Rightarrow n_2= 88.89,故選\bbox[red,2pt]{(A)}$$
解答:$${n_1 \over (z_{\alpha_1/2})^2} = {n_2 \over (z_{\alpha_2/2})^2} \Rightarrow {175 \over 1.96^2} ={n_2 \over 1.645^2} \Rightarrow n_2= 123.27,故選\bbox[red,2pt]{(C)}$$
解答:$$顯著水準=0.05,經查表P(Z\gt 1.645)=0.05 \Rightarrow 臨界值=100+1.645=101.645\\,而現在為103,與臨界值相差103-101.645=1.355 \Rightarrow P(Z\gt 1.355)\approx 0.09,故選\bbox[red,2pt]{(B)}$$
解答:$$依柴比雪夫不等式:P(|X-\mu|\ge b) \le {\sigma^2 \over b^2} \Rightarrow P(|X-70|\ge 10) \le {5^2 \over 10^2}=25\%\\ 因此P(60\le X\le 80)= P( |X-70|\le 10) = 1- P(|X-70|\ge 10)=1-25\% = 75\%\\ \Rightarrow 600\times 75\% =450,故選\bbox[red,2pt]{(D)}$$
======================= END =====================
解題僅供參考,其他專科學力鑑定試題及詳解















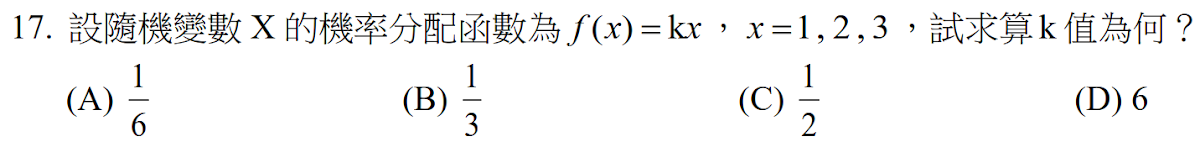
































沒有留言:
張貼留言