教育部108年自學進修專科學校學力鑑定考試
專業科目(一): 初級統計
解答:$$信用評比有高低之分,故選\bbox[red,2pt]{(D)}$$
解答:$$85-95分在中位數與Q_3之間,占全部的{1\over 4},故選\bbox[red,2pt]{(A)}$$
解答:$$強調x軸與y軸間的關係,故選\bbox[red,2pt]{(C)}$$
解答:$$薪資\color{blue}{樣本}標準差=\sqrt{\sum (x_i-\bar x)^2\over n-1} =\sqrt{\sum X^2-(\sum X)^2/n \over n-1} \\=\sqrt{92.6-(30)^2/10\over 9} =\sqrt{2.6\over 9} =0.5374,故選\bbox[red,2pt]{(D)}$$
解答:$$\cases{甲班變異係數=5/65=1/13\\ 乙班變異係數=7/98=1/14} \Rightarrow 甲\gt 乙,故選\bbox[red,2pt]{(A)}$$
解答:$$5名學生智力測驗由小至大為:90,120,140,145,160;\cases{5/4=1.25 \Rightarrow Q_1=第2位=120\\ 5\times 3/4= 3.75 \Rightarrow Q_3=第4位=145} \\ \Rightarrow Q_3-Q_1=145-120=25,故選\bbox[red,2pt]{(B)}$$解答:$$平均數\gt 中位數 \gt 眾數\Rightarrow 右偏,故選\bbox[red,2pt]{(A)}$$
解答:$$(A)\bigcirc:\cases{P(A)=0.6 \\ P(B)=0.4} \Rightarrow P(B\mid A)=0.3 = {P(A\cap B) \over P(A)} ={P(A\cap B)\over 0.6} \Rightarrow P(A\cap B)= 0.18 \\(B)\bigcirc: P(A\cap B^c)=P(A)-P(A\cap B)=0.6-0.18=0.42 \\(C)\bigcirc: P(A\mid B)= {P(A\cap B)\over P(B)} ={0.18\over 0.4}= 0.45 \\(D)\times: P(A\cup B)= P(A)+P(B)-P(A\cap B)=0.6+0.4 -0.18=0.82 \ne 0.72\\,故選\bbox[red,2pt]{(D)}$$
解答:$${50\% \times 30\% \over 50\% \times 30\% +30\% \times 20\% +20\% \times 10\% } ={15 \over 15+6+2} ={15\over 23}=0.652,故選\bbox[red,2pt]{(D)}$$
解答:$$V(W)=V(3X+5Y) = 3^2V(X) +5^2V(Y) =9\times 4+25\times 4=136,故選\bbox[red,2pt]{(D)}$$
解答:$$\sum f(x)=1 \Rightarrow f(1)+f(2)+ f(3)+f(4) = 4c+3c+2c +c=1 \Rightarrow c=1/10\\ 又\cases{EX = \sum xf(x) = 4c+6c+6c+4c= 20c=2\\ EX^2 = \sum x^2f(x)=4c+12c+ 18c+ 16c=50c =5} \\\Rightarrow V(X)=EX^2-(EX)^2 =5-2^2=1,故選\bbox[red,2pt]{(A)}$$
解答:$$10000\times 0.1-500 =500,故選\bbox[red,2pt]{(B)}$$
解答:$$X\sim B(10,0.03) \Rightarrow Var(X)=np(1-p)= 10\times 0.03\times 0.97 =0.291,故選\bbox[red,2pt]{(C)}$$
解答:$${抽到1件良品及抽到1件不良品\over 9件任取2件} ={C^5_1C^4_1\over C^9_2} ={5\over 9} =0.5556,故選\bbox[red,2pt]{(D)}$$
解答:$$第一次:正正正、反反反\Rightarrow 機率為{1\over 8}+{1\over 8}={1\over 4}\\ 第二次:與第一次結果相反\Rightarrow 機率為1-{1\over 4}={3\over 4} \\ 因此機率為{1\over 4}\times {3\over 4}={3\over 16}= 0.1875,故選\bbox[red,2pt]{(B)}$$
解答:$$X\sim P \Rightarrow P(X=k)= {e^{-\lambda}\;\lambda^k \over k!},\lambda=2\\最多發生一次=發生0次或1次,即P(k=0)+P(k=1) = e^{-\lambda} +\lambda \cdot e^{-\lambda} =3 e^{-2}\\ = 3\times 0.1353=0.4059,故選\bbox[red,2pt]{(D)}$$
解答:$$(A)\times: X為連續隨機變數,因此無單點機率,即P(X=C)不存在\\ (B)\times: P(X=C)不存在\\ (C)\times: 機率總和為1,並非期望值為1\\(D)\bigcirc:,X為連續隨機變數,因此P(X\le C)=P(X\lt C)\\故選\bbox[red,2pt]{(D)}$$
解答:$$P(X\lt 320) = P(Z\lt {320-400\over 80 }) =P(Z\lt -1) =P(Z\gt 1) =P(Z\gt 0)-P(0\lt Z\lt 1)\\= 0.5-P(0\lt Z\lt 1) =0.5-0.3413= 0.1587,故選\bbox[red,2pt]{(B)}$$
解答:$$P(0\lt Z\lt 1.64)=0.4495 \Rightarrow P(Z\lt 1.64)=0.5+0.4495 =0.9495 \Rightarrow P(Z\gt 1.64)\approx 0.05\\ 因此{X-250\over 30} =1.64 \Rightarrow X=299.2,故選\bbox[red,2pt]{(C)}$$
解答:$$常態分配為左右對稱,平均數左、右邊面積均為0.5,故選\bbox[red,2pt]{(D)}$$
解答:$$\cases{\int f(x)\;dx=1 \Rightarrow \int_0^1 a+bx\;dx =\left. \left[ ax+{1\over 2}bx^2 \right] \right|_0^1 =a+{1\over 2}b=1 \\\int xf(x)\;dx=1/2 \Rightarrow \int_0^1 x(a+bx)\;dx =\left. \left[ {1\over 2}ax^2+{1\over 3}bx^3 \right] \right|_0^1 = {1\over 2}a +{1\over 3}b={1\over 2} } \\ \Rightarrow \cases{2a+b= 2\\ 3a+2b=3} \Rightarrow \cases{a=1\\ b=0 },故選\bbox[red,2pt]{(C)}$$
解答:$$一個人體重X\sim N(60,10^2) \Rightarrow 16人體重Y \sim N(60\times 16, 10^2\times 16) =N(960,1600)\\ 欲求K值滿足P(Y\gt K)=1\%,即P(Z\gt {K-960 \over \sqrt{1600}})=1\% \Rightarrow {K-960 \over 40}=2.326\\ \Rightarrow K=1053.04,故選\bbox[red,2pt]{(B)}\\ 可是公布的答案是\bbox[blue,2pt]{(C)}$$
解答:$$\cases{X\sim N(5,3^2)\\ Y\sim N(10,4^2)} \Rightarrow Y-X \sim N(10-5,3^2+4^2)=N(5,5^2)\\ \Rightarrow P(Y-X\gt -3)= P(Z \gt {-3-5\over 5}) = P(Z\gt -1.6)= P(-1.6 \lt Z\lt 0)+0.5 \\=P(0\lt Z\lt 1.6)+0.5 =0.4452+0.5=0.9452,故選\bbox[red,2pt]{(C)}$$
解答:$$依中央極限定理的定義,故選\bbox[red,2pt]{(C)}$$
解答:$$n\ge (z_{\alpha/2})^2 \cdot {\sigma^2 \over E^2} = (z_{0.025})^2\cdot {550^2\over 150^2} =1.96^2\cdot {11^2\over 3^2}= 51.65 \Rightarrow n=52,故選\bbox[red,2pt]{(C)}$$
解答:$$P(0\lt Z\lt 1.64)=0.4495 \Rightarrow P(Z\lt 1.64)=0.5+0.4495 = 0.9495 \Rightarrow P(Z\gt 1.64)=0.05\\信賴區間長度=2z_{\alpha/2}\cdot \sqrt{p(1-p)\over n} =2z_{0.05}\cdot \sqrt{(180/300)(120/300)\over 300}\\= 2\times 1.64\times 0.0283 = 0.09277\\只有選項(C)的區間長度0.646-0.553=0.093,故選\bbox[red,2pt]{(C)}$$
解答:$$\cases{P(0\lt Z\lt 1.64)=0.4495\\ P(0\lt Z\lt 1.65)=0.4505} \Rightarrow P(0\lt Z\lt {1.64+1.65\over 2}=1.645)= 0.95\\n\ge {(z_{\alpha/2})^2}\times {p(1-p)\over E^2} =1.645^2 \times {0.4\times 0.6 \over 0.05^2} = 259.78 \Rightarrow n=260,故選\bbox[red,2pt]{(A)}$$
解答:$$樣本數增加,抽樣誤差減少,也就是信賴區間縮短,信心水準提升;\\而母體的統計資料不會改變,故選\bbox[red,2pt]{(A)}$$
解答:$$樣本趨近無限大時,估計值與母體資料會趨於一致,稱為一致性,故選\bbox[red,2pt]{(D)}$$
解答:$$目前平均銷售量為14,因此只考慮選項(B)與(D);\\又拒絕H_0需較謹慎,因此若能拒絕H_0表示計畫真正成功機率較高,故選\bbox[red,2pt]{(D)}$$
解答:$$P(X\lt 5) =P(Z\lt {5-4.9\over 0.5/\sqrt{25}}) = P(Z\lt 1)\\由於P(0\lt Z\lt 1)=0.3413 \Rightarrow P值為P(Z\gt 1)=0.5-0.3413 =0.1587,故選\bbox[red,2pt]{(A)}$$
解答:$$(A)\times: 虛無假設為真時,拒絕虛無假設\\ (C)\times: 拒絕的機率\\(D)\times: 當對立假設為真時,拒絕虛無假設的機率\\,故選\bbox[red,2pt]{(B)}$$
解答:$$母體變異數未知\Rightarrow T檢定;又考量每個人的減肥前後,因此是配對的,故選\bbox[red,2pt]{(C)}$$
解答:$$P \lt \alpha \Rightarrow 已達顯著水準 \Rightarrow 拒絕H_0,故選\bbox[red,2pt]{(B)}$$
解答:$${9.8-8\over {4.2\over \sqrt{15}}} ={3\sqrt{15}\over 7} =1.659,故選\bbox[red,2pt]{(B)}$$
解答:$${\bar x_1-\bar x_2\over \sqrt{{s_1^2 \over n_1} +{s_2^2\over n_2}}} ={87-83 \over \sqrt{{12 \over 10}+{10\over 10}}} ={4\over \sqrt{2.2}} = 2.697,故選\bbox[red,2pt]{(B)}$$
解答:$$題目未給顯著水準,\bbox[blue,2pt]{無法作答},公布的答案是\bbox[red,2pt]{(A)}$$
解答:$$\begin{array}{|c|c|c|c|} \hline 變異來源 & 自由度(df) & 平方和(SS) & 均方(MS) & F\\\hline 塑身處方 & df_B & 26.13 & MS_B\\\hline 隨機誤差 & df_W & 11.6 & MS_W \\\hline 合計\text{Total} & 14 \\\hline\end{array}\\ 因此\cases{df_B= 3-1=2 \\ df_W= 14-df_B=14-2=12} \Rightarrow \cases{MS_B= 26.13/df_B= 26.13/2 \\ MS_W= 11.6/df_W= 11.6/12} \\ \Rightarrow F=MS_B/MS_W= {26.13\over 2}\times {12 \over 11.6} =13.515,故選\bbox[red,2pt]{(D)}$$
解答:$$依題意\cases{k=4\\ n=4+5+3+5=17\\ \alpha=0.05} \Rightarrow \cases{df_B=4-1=3\\ df_W=17-4=13} \Rightarrow F_{df_B,df_W,\alpha} =F_{3,13,0.05},故選\bbox[red,2pt]{(A)}$$
解答:$$觀察值\Rightarrow \begin{array}{} & 合格 & 不良 & 小計\\\hline 第1班& 368 & 32 & 400\\ 第2班& 285 & 15 & 300\\ 第3班& 176 & 24 & 200\\\hline 小計 & 829 & 71 & 900 \end{array}\\ 期望值\Rightarrow \begin{array}{} & 合格 & 不良 & 小計\\\hline 第1班& 829\times {4\over 9}=368.44 & 71\times {4\over 9}=31.56 & 400\\ 第2班& 829\times {3\over 9}=276.33 & 71\times {3\over 9}=23.67 & 300\\ 第3班& 829\times {2\over 9}=184.22 & 71\times {2\over 9}=15.78 & 200\\\hline 小計 & 829 & 71 & 900 \end{array}\\ \chi^2 ={(368.44-368)^2\over 368.44} +{(31.56-32)^2 \over 31.56} +{(276.33-285)^2\over 276.33} +{(23.67-15)^2 \over 23.67} \\\qquad \quad +{(184.22-176)^2\over 184.22} +{(15.78-24)^2 \over 15.78} \\={0.44^2 \over 368.44} +{0.44^2\over 31.56} +{8.67^2\over 276.33} +{8.67^2\over 23.67} +{8.22^2 \over 184.22} +{8.22^2 \over 15.78} \approx 8.1,\bbox[red,2pt]{選項無此答案}\\但0.44^2\times 2 +8.67^2\times 2 +8.22^2\times 2 \approx 285.86\to 選項\bbox[blue,2pt]{(D)}$$
解答:$$\cases{\bar x= (2+4+1+5+3) \div 5 =3\\ \bar y =(15+25+10+ 40+30)\div 5=24} ,由於迴歸直線經過(\bar x,\bar y)=(3,24)\\,也就是X=3時,Y=24,故選\bbox[red,2pt]{(C)}$$
解答:$$廣告支出越多,銷售量越大,兩者為正相關,故選\bbox[red,2pt]{(B)}$$
解答:$$(A)\times:判定係數=SSR/SST皆為正值\\(B)\times:與相關係數不同 \\(D)\times: SSE=SST-SSR,因此SSE越小代表SSR與SST越接近,\\\quad 判定係數也越接近1,即係數變大\\故選\bbox[red,2pt]{(C)}$$
解答:$$\cases{MSE=10\\ n=50} \Rightarrow SSE=MSE \times (n-k) = 10\times (50-2)=480 \\\Rightarrow SSR=SST-SSE = 2000-480=1520\\ \Rightarrow R^2= SSR/SST = 1520/2000=0.76,故選\bbox[red,2pt]{(B)}$$
解答:$$擔任主管且為女生有40名,抽樣數為200,因此機率為{40\over 200}=0.2,故選\bbox[red,2pt]{(D)}$$
解答:$$P(擔任主管\mid 性別=女)= {擔任主管且為女性\over 女性} ={40\over 100} =0.4,故選\bbox[red,2pt]{(B)}$$
解答:$$\cases{P(擔任主管)= {90\over 200} \\P(女性)={1\over 2} \\ P(擔任主管且為女性) ={40\over 200} } \\\Rightarrow P(擔任主管)\times P(女性) ={90\over 200}\times {1\over 2}={45\over 200} \ne P(擔任主管且為女性) ={40\over 200}\\ \Rightarrow 主管職位與性別不獨立,故選\bbox[red,2pt]{(B)}$$
解答:$$X=250 \Rightarrow Z={250-125\over 64} =1.95;\\由P(0\le Z\lt 1.95)=0.4744可知X=250超過考生比例=0.5+0.4744 = 0.9744 \\ \Rightarrow 人數為0.9744\times 4500 = 4384.8 \Rightarrow 排名為4500-4384.8=115.2,故選\bbox[red,2pt]{(C)}$$
解答:$${500\over 4500}={1\over 9}=0.1111 \Rightarrow 成績要超過比偷為1-0.1111= 0.8889的考生分數\\,也就是要找k值滿足P(Z\lt k)=0.8889; 由於P(0\le Z\le 1.22)=0.3888 \\\Rightarrow P(Z\le 1.22)=0.5+0.3888=0.8888 \Rightarrow k=1.22\\ z分數為1.22 \Rightarrow {X-125\over 64}=1.22 \Rightarrow X=203.08 \Rightarrow 要考204分才會被錄取,故選\bbox[red,2pt]{(A)}$$
================= end =====================














































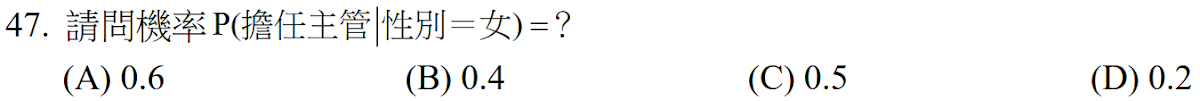



沒有留言:
張貼留言