102 學年度身心障礙學生升學大專校院甄試甄試類(群)組別:四技二專組-數學(C)
單選題,共 20 題,每題 5 分
解答:$$\alpha,\beta為2x^2+5x+1=0的兩根 \Rightarrow \cases{\alpha +\beta = -5/2\\ \alpha\beta = 1/2} \Rightarrow {1\over \alpha}+ {1\over \beta} ={\alpha+\beta \over \alpha\beta} ={-5/2\over 1/2} =-5\\,故選\bbox[red,2pt]{(A)}$$
解答:$$x^2+ y^2-2x+6y+9=0 \Rightarrow (x-1)^2 +(y+3)^2=1 \Rightarrow \cases{圓心O(1,-3)\\ 半徑r=1} \\ \Rightarrow \overline{OP} =\sqrt{3^2+4^2} =5 \Rightarrow P到圓最短距離=5-r= 4,故選\bbox[red,2pt]{(C)}$$
解答:$$2x^2 +x-3 =(2x+3)(x-1) =(2x-n)(x-m) \Rightarrow \cases{m=1\\ n=-3} \Rightarrow m-n=4,故選\bbox[red,2pt]{(D)}$$
解答:$$\cases{A(1,2)\\ B(t,3)\\ C(t+2,-1)} \Rightarrow \cases{\overrightarrow{AB}= (t-1,1)\\ \overrightarrow{AC} =(t+1,-3)} ,由於 \overrightarrow{AB}\parallel \overrightarrow{AC} \Rightarrow {t-1\over t+1}={1\over -3} \Rightarrow -3t+3=t+1\\ \Rightarrow t={1\over 2},故選\bbox[red,2pt]{(C)}$$
解答:$$\cos \angle A = {\overline{AB}^2 +\overline{AC}^2 -\overline{BC}^2 \over 2\cdot \overline{AB}\cdot \overline{AC}} \Rightarrow \cos 60^\circ = {3^2+4^2- \overline{BC}^2 \over 2\cdot 3\cdot 4} \Rightarrow \overline{BC}^2 =25-12=13 \\\Rightarrow \overline{BC} =\sqrt{13},故選\bbox[red,2pt]{(A)}$$
解答:$$f(k)=0 \Rightarrow k^2-k-6=0 \Rightarrow (k-3)(k+2)=0 \Rightarrow k=3或-2 \\\Rightarrow \cases{g(3) = 27-18-3-6=0\\ g(-2)= -8-8 +2-6\ne 0} \Rightarrow f(3)=g(3)=0 \Rightarrow k=3,故選\bbox[red,2pt]{(D)}$$
解答:$$\cases{\vec a=(x,-1)\\ \vec b=(2,-3)} \Rightarrow \vec a\cdot \vec b=2x+3= -5\Rightarrow x=-4,故選\bbox[red,2pt]{(A)}$$
解答:$$\cases{1=\log_a (5-2)\\ 3=\log_a (b-2)} \Rightarrow \cases{a=3\\ a^3=b-2 }\Rightarrow b=a^3+2=29 \Rightarrow a+b= 3+29=32,故選\bbox[red,2pt]{(C)}$$
解答:$$\cos\theta -\sin \theta =-\sqrt 2\Rightarrow (\cos\theta -\sin\theta)^2 =1-2\sin\theta \cos\theta =2 \Rightarrow \sin\theta \cos\theta \lt 0\\ 由\cases{\cos\theta -\sin\theta \lt 0\\ \sin\theta \cos\theta \lt 0} \Rightarrow \cases{\cos \theta \lt 0\\ \sin\theta \gt 0} \Rightarrow \theta 在第二象限,故選\bbox[red,2pt]{(B)}$$
解答:$$2x+y=1的斜率為-2,與其垂直的斜率為1/2,且通過(2,1)的直線為y={1\over 2}(x-2)+1\\ \Rightarrow x=2y,故選\bbox[red,2pt]{(D)}$$
解答:$$6為x+2和x-3的等比中項\Rightarrow 6^2=(x+2)(x-3) \Rightarrow x^2-x-42=0 \Rightarrow (x-7)(x+6)=0\\ \Rightarrow x=-6,故選\bbox[red,2pt]{(B)}$$
解答:$$\cases{A(-2,-3)\\ B(1,-1) \\ C(c,0)} \Rightarrow \cases{\overrightarrow{AB} =(3,2) \\ \overrightarrow{AC} =(c+2,3)},又\angle A=90^\circ \Rightarrow \overrightarrow{AB} \cdot \overrightarrow{AC} =3c+6+6=0 \Rightarrow c=-4\\,故選\bbox[red,2pt]{(A)}$$
解答:$$\cases{取出1紅1綠的次數:C^3_1C^2_1 =6\\ 取出1綠1白的次數:C^2_1C^4_1 =8\\ 取出1紅1白的次數:C^3_1C^4_1 =12} \Rightarrow 取出不同色的機率=(6+8+12)/C^9_2 =26/36 =13/18\\,故選\bbox[red,2pt]{(D)}$$
解答:$$(\sin \theta +\cos \theta)^2 =1+2\sin\theta \cos\theta= 1+2\cdot {3\over 8} ={7\over 4} \Rightarrow \sin\theta +\cos\theta ={\sqrt 7\over 2},故選\bbox[red,2pt]{(C)}$$
解答:$$2\cdot 2^{2x}+3\cdot 2^x-2 =0 \Rightarrow 2\cdot (2^{x})^2+3\cdot 2^x-2 =0 \Rightarrow (2\cdot 2^x-1)(2^x+2)=0 \Rightarrow 2^x={1\over 2}\\ \Rightarrow x=-1,故選\bbox[red,2pt]{(B)}$$
解答:$$x^2-x-12\lt 0 \Rightarrow (x-4)(x+3)\lt 0 \Rightarrow -3\lt x\lt 4,故選\bbox[red,2pt]{(D)}$$
解答:$$a_{n+1}-a_n=2 \Rightarrow a_{10}=a_9+2 = a_8+2+2=\cdots =a_1+2\times 9=1+18=19,故選\bbox[red,2pt]{(C)}$$
解答:$$不考慮甲乙丙,剩下四人任排有4!=24種排法;\\甲乙兩人排在最前頭,可以是甲乙或乙甲兩種排法;\\而丙一定是排在最後,因此共有24\times 2=48種排法,故選\bbox[red,2pt]{(B)}$$
解答:$$x^2+y^2 -6x+4y+4=0 \Rightarrow (x-3)^2 +(y+2)^2 =3^2 \Rightarrow \cases{圓心P(3,-2)\\ 半徑r=3} \\ \Rightarrow \overline{OP} =\sqrt{3^2+(-2)^2} =\sqrt{13} \Rightarrow \overline{OA}^2 = \overline{OP}^2-r^2 =13-9=4 \Rightarrow \overline{OA} =\sqrt 4=2,故選\bbox[red,2pt]{(A)}$$
========================= END ==============================
解題僅供參考,其他歷屆試題及詳解






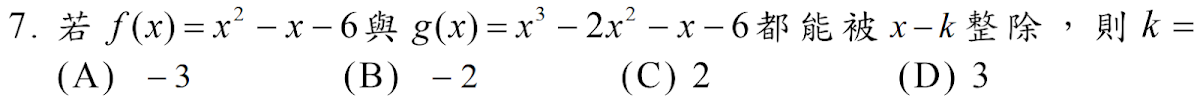


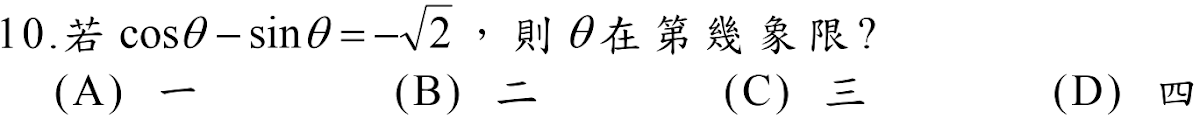









沒有留言:
張貼留言