104 學年度身心障礙學生升學大專校院甄試
甄試類(群)組別:四技二專組-數學(C)
單選題,共 20 題,每題 5 分
解答:$$a= \cos 135^\circ\cos 15^\circ -\sin 135^\circ \sin 15^\circ =\cos(135^\circ+15^\circ) =\cos 150^\circ =-\cos 30^\circ = -{\sqrt 3\over 2}\\,故選\bbox[red,2pt]{(B)}$$
解答:$$\cases{\vec a=(2,-5) \\ \vec b=(-2,6)\\ \vec c=(x,y)} \Rightarrow 3(\vec c+\vec a)= 4(\vec c+\vec b) \Rightarrow (3(x+2),3(y-5)) = (4(x-2),4(y+6)) \\ \Rightarrow \cases{3x+6=4x-8\\ 3y-15=4y+24} \Rightarrow \cases{x= 14\\ y=-39} \Rightarrow \vec c=(14,-39),故選\bbox[red,2pt]{(D)}$$
解答:$$\cases{A(3,2)\\ B(-1,0)\\ C(6,1)} \Rightarrow \cases{a=\overline{BC} =5\sqrt 2\\ b=\overline{AC} =\sqrt{10}\\ c=\overline{AB} =2\sqrt 5} \Rightarrow \cos A={b^2+c^2-a^2\over 2bc} =-{1\over \sqrt 2} \Rightarrow \sin A={1\over \sqrt 2},故選\bbox[red,2pt]{(B)}$$
解答:$$\sqrt 3-i =2({\sqrt 3\over 2}-{1\over 2}i) =\sqrt 2(\cos {11\pi \over 6}+i\sin{11\pi \over 6}) \Rightarrow 主幅角={11 \pi \over 6},故選\bbox[red,2pt]{(C)}$$
解答:$$-3x\gt 4x^2-1 \Rightarrow 4x^2+3x-1\lt 0 \Rightarrow (4x-1)(x+1)\lt 0 \Rightarrow -1\lt x\lt {1\over 4} ,故選\bbox[red,2pt]{(D)}$$
解答:$$\cases{x=\sqrt 3-\sqrt 2\\ y=\sqrt 3+\sqrt 2} \Rightarrow \cases{x^2+y^2=10 \\ xy=1} \Rightarrow {x\over y}+{y\over x}= {x^2+y^2 \over xy} ={10\over 1}=10,故選\bbox[red,2pt]{(D)}$$
解答:$$f(x)= x^4-3x^3+x^2 +x+1 = (x^2+x-2)p(x)+ ax+b\\ \Rightarrow \cases{f(-2)=16+24+4-2+1=45 =-2a+b\\ f(1)=1-3+1+1+1=1=a+b} \Rightarrow \cases{a=-44/3\\ b=47/3} \Rightarrow a+b=1,故選\bbox[red,2pt]{(A)}$$
解答:$$\left|\begin{matrix}200 & 201 & 202\\201 & 202 & 203\\202 & 203 & 202\end{matrix}\right| \xrightarrow{-r_1+r_2,-r_1+r_3} \left|\begin{matrix}200 & 201 & 202\\1 & 1 & 1\\2 & 2 & 0\end{matrix}\right| \xrightarrow{-200r_2+r_1,-2r_2+r_3} \left|\begin{matrix}0 & 1 & 2\\1 & 1 & 1\\0 & 0 & -2\end{matrix}\right|= 2,故選\bbox[red,2pt]{(B)}$$
解答:$$(x^2-2x)^2-9(x^2-2x)+18 =(x^2-2x-6)(x^2-2x-3) =(x^2-2x-6)(x-3)(x+1)\\ \Rightarrow x-3為其因式,故選\bbox[red,2pt]{(B)}$$
解答:$$(-{7\over 3})+ (-{5\over 3})+(-1)+(-{1\over 3})+{1\over 3}+1+{5\over 3}+{7\over 3}+{9\over 3}+{11\over 3} \\ ={9\over 3}+{11\over 3}={20\over 3},故選\bbox[red,2pt]{(C)}$$
解答:$$f(x)={2^x+2^{-x}\over 3^x+3^{-x}} \Rightarrow \cases{(A)\times: f(0)={1+1\over 1+1}= 1 \ne {2\over 3}\\[1ex] (B)\times:f(1)={2+1/2\over 3+1/3} ={3\over 4}\ne {2\over 3}\\[1ex] (C)\bigcirc:f(-1)=f(1)={3\over 4} \\[1ex](D)\times: f(2)={4+1/4\over 9+1/9} ={153\over 328} \ne {3\over 4}}\\,故選\bbox[red,2pt]{(C)}$$
解答:$$環狀排列:4!/4= 6,故選\bbox[red,2pt]{(D)}$$
解答:$$(A)\times: S=\{(1,1),(1,2),\dots,(6,6)\}\\(B)\bigcirc: \{(a,b)\mid a,b其中之一是偶數,且1\le a,b,\le 6\},共3\times 3+3\times 6=27 \Rightarrow 機率為27/36= 3/4\\(C)\times: \{(a,b)\mid a,b同為偶數或同為奇數\},共3\times 3+3\times 3=18\Rightarrow 機率為18/36= 1/2\\(D)\times: (1,1),(1,2),(1,4),(1,6),(2,3),(2,5),(3,4),(5,6)及其排列,共16個\Rightarrow 機率16/36=4/9\\,故選\bbox[red,2pt]{(B)}$$
解答:$$ 資料依序排列\Rightarrow \begin{array}{|c|rrrrrrrr|}\hline i& 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8\\ \hdashline x_i& 7 & 7 & 10 & 12 & 12 & 12 & 13 & 15\\ \hdashline x_i-\bar x&-4 & -4 & -1 & 1 & 1 & 1 & 2 & 4\\ \hdashline (x_i-\bar x)^2 &16 & 16 & 1 & 1 & 1 & 1 & 4 & 16 \\\hline\end{array}\\ \Rightarrow \cases{(A)\bigcirc:\sum_{i=1}^{8} x_i =88 \Rightarrow 平均值 \bar x=88/8=11 \\[1ex](B)\times: 12出現3次,7出現2次,因此12為眾數\\[1ex](C)\times: 中位數=(x_4+x_5)\div 2=12\\[1ex] (D)\times: 標準差=\sqrt{\sum(x_i-\bar x)^2 \over n} =\sqrt{56\over 8} =\sqrt 7}\\,故選\bbox[red,2pt]{(A)}$$
解答:$$圓心(0,0)至直線的距離等於圓半徑(r=5),則直線與圓相切\\(A)\bigcirc: {5^2\over 5}=5=r\\(B)\times: {5^2\over \sqrt{13}} \ne r\\ (C)\times: {5\over 5}=1 \ne r\\ (D)\times: {5\over \sqrt{13}} \ne r\\,故選\bbox[red,2pt]{(A)}$$
解答:$${x^2\over 2}-{y^2 \over 3}=5 \Rightarrow {x^2\over 10}-{y^2 \over 15}=1 \Rightarrow a^2=10 \Rightarrow a=\sqrt{10} \Rightarrow |\overline{PF_1}-\overline{PF_2}|= 2a=2\sqrt{10}\\,故選\bbox[red,2pt]{(A)}$$
解答:$$\lim_{x\to 0}{ {1\over 2+x}-{1\over 2}\over x} =\lim_{x\to 0}{ {-x\over 2(2+x)} \over x} =\lim_{x\to 0}{-1\over 2(2+x)} =-{1\over 4},故選\bbox[red,2pt]{(A)}$$
解答:$$\lim_{n\to \infty} {3n+2n^2-5\over -n^2-4n+1}= \lim_{n\to \infty} {3/n+2 -5/n^2\over -1-4/n+1/n^2} ={0+2-0\over -1-0+0} =-2,故選\bbox[red,2pt]{(B)}$$
解答:$$最大面積為正方形,其邊長總和為20,因此邊長=20\div 4=5 \Rightarrow 面積=5^2=25,故選\bbox[red,2pt]{(C)}$$
============================ END ===============================
解題僅供參考,其他歷屆試題及詳解

















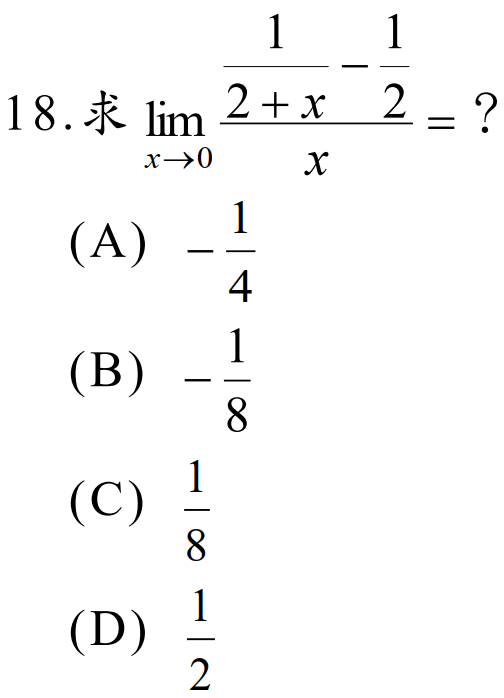


沒有留言:
張貼留言