：$$x^7-xy+y^9=1 \Rightarrow {d\over dx} (x^7-xy+y^9) =7x^6-y-x{dy\over dx}+9y^8 {dy\over dx} =0 \Rightarrow {dy\over dx} ={ y-7x^6\over 9y^8-x} \\ \Rightarrow \left. {dy\over dx} \right|_{(1,1)} ={1-7\over 9-1} =-{3\over 4}，故選\bbox[red, 2pt]{(A)}$$
解答：$$f(x)=x^4-x^2 \Rightarrow f'(x)=4x^3-2x，因此f'(x)=0 \Rightarrow 2x(2x^2-1)=0 \Rightarrow x=0,\pm 1/\sqrt 2 \\ \Rightarrow \cases{f(0)= 0\\ f(1/\sqrt 2)={1\over 4}-{1\over 2} =-{1\over 4}\\ -1/\sqrt 2\not \in [0,1] \Rightarrow 不考慮f(-1/\sqrt 2)} \Rightarrow 最小值為－{1\over 4}，故選\bbox[red, 2pt]{(C)}$$
解答：$$取\cases{u=x \Rightarrow du=dx\\ dv=e^{-x}dx \Rightarrow v=-e^{-x}}，則\int xe^{-x}\,dx = -xe^{-x} +\int e^{-x}\,dx = -xe^{-x} -e^{-x} +C\\ \Rightarrow \int_0^1 xe^{-x}\,dx = \left. \left[ -xe^{-x} -e^{-x} \right] \right|_0^1 =-e^{-1}-e^{-1}-(-1) =1-2e^{-1}，故選\bbox[red, 2pt]{(B)}$$
解答：$$y'=4x \Rightarrow y=2x^2+C 且通過(2,9) \Rightarrow 9=8+C \Rightarrow C=1 \Rightarrow y=2x^2+1，故選\bbox[red, 2pt]{(C)}$$
解答：$$g(x,y) ={\sin x\over e^x +y^2} \Rightarrow g_x= {\cos x\over e^x +y^2} -{\sin x\over (e^x+y^2)^2} \cdot e^x \Rightarrow g_x(0,1)= {1\over 1+1}-0 ={1\over 2}，故選\bbox[red, 2pt]{(A)}$$
解答：$$F(x) = \int_{4}^{x^2} \sqrt{t^2+8} \,dt \Rightarrow F'(x)=\sqrt{x^4+8}\cdot 2x \Rightarrow F'(-1) =\sqrt 9 \cdot (-2) =-6，故選\bbox[red, 2pt]{(A)}$$
解答：$$改變積分順序，\int_0^2 \int_{y/2}^1 e^{x^2}\,dxdy = \int_0^1 \int_0^{2x} e^{x^2}\,dydx =\int_0^1 2xe^{x^2}\,dx =\left. \left[ e^{x^2} \right]\right|_0^1 =e-1\\，故選\bbox[red, 2pt]{(C)}$$
解答：$$0\le \left| x^{10} \sin{1\over x}\right| \le x^{10} \Rightarrow \lim_{x\to 0}x^{10} \sin{1\over x} =0 \Rightarrow f(0)=0，故選\bbox[red, 2pt]{(B)}$$
解答：$$g(x)={x^2+x+1 \over x^3+x^2+x+1} \Rightarrow g'(x)={2x+1\over x^3+x^2+x+1 } -{x^2+x+1\over (x^3+x^2+x+1)^2} \cdot (3x^2+2x+1) \\\Rightarrow g'(1)={3\over 4}-{3\over 16} \cdot 6 ={3\over 4}- {9\over 8} =-{3\over 8}，故選\bbox[red, 2pt]{(D)}$$
解答：$$ \lim_{x \to \infty} {\ln x\over x^{1/111}} = \lim_{x \to \infty} {(\ln x)' \over (x^{1/111})'} =\lim_{x \to \infty} {1/x \over {1\over 111}x^{-110/111}} = \lim_{x \to \infty} {111 \over x^{1/111}} = 0，故選\bbox[red, 2pt]{(A)}$$
解答：$$f(x)=xe^{-x^2/2} \Rightarrow f'(x)=e^{-x^2/2}-x^2 e^{-x^2/2} =e^{-x^2/2}(1-x^2)\\ 因此f'(x) =0 \Rightarrow x^2=1 \Rightarrow x=\pm 1，故選\bbox[red, 2pt]{(B)}$$
解答：$$f(x,y)=\sin x \cos y \Rightarrow \cases{f_x= \cos x\cos y\\ f_y=-\sin x\sin y} \Rightarrow \cases{f_{xx}= -\sin x\cos y\\ f_{yy}= -\sin x\cos y\\ f_{xy} =-\cos x\sin y} \\\Rightarrow d(x,y)= f_{xx}f_{yy}-f_{xy}^2 = (\sin x \cos y)^2-(\cos x\sin y)^2 \Rightarrow d(\pi/2,\pi) = 1\gt 0 \\ \Rightarrow f(\pi/2, \pi)為相對極小值，故選\bbox[red, 2pt]{(B)}$$
解答：$$\int_{-2}^{-1} {2x+4 \over x^2(x-2)} \,dx = \int_{-2}^{-1} \left( -{2\over x}-{2\over x^2} +{2\over x-2 }\right) \,dx =\left. \left[ -2\ln x+{2\over x}+ 2\ln(x-2)\right]\right|_{-2}^{-1} \\=\left. \left[ \ln {(x-2)^2\over x^2} +{2\over x} \right]\right|_{-2}^{-1} =\ln 9-2-(\ln 16-1) =2\ln 3-2\ln 2-3= 2\ln{3\over 2}-1，故選\bbox[red, 2pt]{(D)}$$
解答：$$y=x \Rightarrow y'=1 \Rightarrow \sqrt{1+y'^2} =\sqrt{2} \Rightarrow 繞x軸旋轉的表面積= \int_0^1 2\pi x \cdot \sqrt 2\,dx =\left.\left[ \sqrt 2\pi x^2 \right]\right|_0^1 \\=\sqrt 2\pi，故選\bbox[red, 2pt]{(B)}$$
解答：$$r=e^{2\theta} \Rightarrow {dr\over d\theta} =2e^{2\theta} \Rightarrow 曲線長＝\int_{\ln 2}^{ \ln 4} \sqrt{r^2 +({dr \over d\theta})^2} \,d\theta ＝\int_{\ln 2}^{ \ln 4} \sqrt{e^{4\theta} +4e^{4\theta}} \,d\theta ＝\int_{\ln 2}^{ \ln 4} \sqrt 5e^{2\theta} \,d\theta \\ =\left.\left[ {1\over 2}\sqrt 5 e^{2\theta} \right] \right|_{\ln 2}^{ \ln 4} ={\sqrt 5\over 2}(16-4) = 6\sqrt 5，故選\bbox[red, 2pt]{(C)}$$
解答：$$f(x)={1\over 1-x} = 1+x+x^2 +\cdots =\sum_{k=0}^\infty x^k \Rightarrow f'(x)=\sum_{k=1}^\infty kx^{k-1} \Rightarrow f''(x)= \sum_{k=2}^\infty k(k-1)x^{k-2} \\\Rightarrow f^{[n]}(x)= \sum_{k=n}^\infty k!x^{k-n} \Rightarrow f^{[k]}(0)=k! \Rightarrow f(x)的泰勒級數＝\sum_{k=0}^\infty {f^{[k]}(0) \over k!}x^k＝\sum_{k=0}^\infty x^k，故選\bbox[red, 2pt]{(D)}$$
解答：$$\lim_{x\to 11}{\sqrt x-\sqrt{11} \over x^2-121} =\lim_{x\to 11}{\sqrt x-\sqrt{11} \over (x+11)(x-11)} = \lim_{x\to 11}{\sqrt x-\sqrt{11} \over (x+11)(\sqrt x-\sqrt{11}) (\sqrt x+\sqrt{11})}\\ = \lim_{x\to 11}{1 \over (x+11) (\sqrt x+\sqrt{11})} ={1\over 22(2\sqrt{11})} ={1\over 44\sqrt{11}}，故選\bbox[red, 2pt]{(D)}$$
解答：$$y=\sqrt x \Rightarrow x=y^2 \Rightarrow 繞Y軸旋轉體積＝\int_0^2 x^2 \pi \,dy =\int_0^2 \pi y^4\,dy =\left.\left[ {\pi \over 5}y^5 \right]\right|_0^2 ={32\over 5}\pi ，故選\bbox[red, 2pt]{(A)}$$
解答：$$\int_0^{2\pi} {1\over 2}r^2\,d\theta =\int_0^{2\pi} 2(1+\cos \theta)^2\,d\theta =\int_0^{2\pi} 2(1+2\cos \theta +\cos^2\theta)\,d\theta \\=\int_0^{2\pi} 2(1+2\cos \theta +{\cos 2\theta+1\over 2})\,d\theta =\int_0^{2\pi} \left(3 +4\cos \theta +\cos 2\theta \right)\,d\theta \\ =\left.\left[ 3\theta+ 4\sin\theta +{1\over 2}\sin 2\theta \right]\right|_0^{2\pi} \ =6\pi，故選\bbox[red, 2pt]{(C)}$$
解答：$$\lim_{x \to \infty} \left( \sqrt{x^2+11x}-x\right) =\lim_{x \to \infty} { (\sqrt{x^2+11x}-x)(\sqrt{x^2+x}+x) \over \sqrt{x^2+x}+x} =\lim_{x \to \infty} {11x \over \sqrt{x^2+x}+x} \\=\lim_{x \to \infty} {11 \over \sqrt{1+1/x}+1} ={11\over 2}，故選\bbox[red, 2pt]{(A)}$$
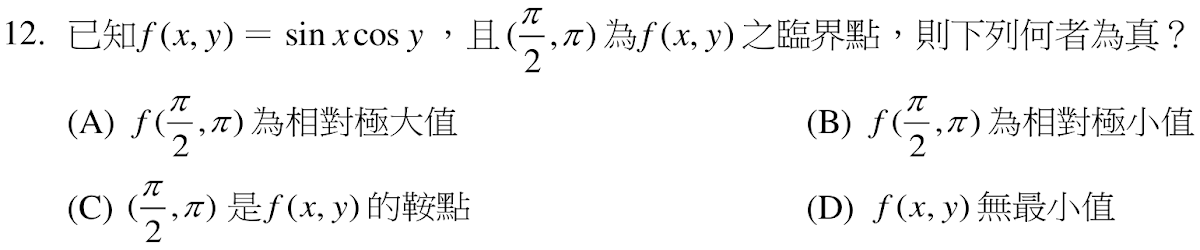
沒有留言:
張貼留言