臺南市 113 學年度市立國民中學正式教師聯合甄選
以下題目共 100 題,為四選一單選選擇題(每題 1 分,共 100 分)
解答:$$可能的情形:春嬌23歲,志明24歲,年齡總和47; 春嬌53歲,志明54歲,年齡總和107,故選\bbox[red, 2pt]{(D)}$$

解答:$$所有的數:11,13,17,19,31,33,37, 39, 71,73,77,79,91,93,97,99,共16個數字,\\其中33,39,77 ,91, 93,99,六個為非質數,剩下10個為質數,因此抽到質數的機率{10\over 16} ={5\over 8}\\,故選\bbox[red, 2pt]{(B)}$$
解答:$$乙\times:三點在都在直線:y=9x-12上\\ 丙:\times:圓心(-1,2)至x軸的距離\ne至y軸距離\\,故選\bbox[red, 2pt]{(C)}$$
解答:$$假設\cases{\overline{AB}=2a\\ \overline{BC}=2b\\ \overline{AC}=2c} \Rightarrow \cases{a\pi= 4\pi\\ {1\over 2}c^2\pi={289\over 8}\pi} \Rightarrow \cases{a=4\\ c={17\over 2}} \\ 又(2a)^2 +(2b)^2 =(2c)^2 \Rightarrow 64+4b^2=289 \Rightarrow b^2={225\over 4} \Rightarrow b={15\over 2},故選\bbox[red, 2pt]{(B)}$$

解答:$${灰色\over 全部} ={10\cdot 8\div 4\over (10+4)\times(8+3)} ={20\over 154} = {10\over 77},故選\bbox[red, 2pt]{(D)}$$

解答:$${0瑕疵+1瑕疵\over 全部}={C^8_3+C^8_2C^2_1 \over C^{10}_3} ={112\over 120} ={14\over 15},故選\bbox[red, 2pt]{(D)}$$
解答:$$\cases{甲=2乙\\ 甲=乙+1\\甲=丙} \Rightarrow \cases{\alpha=2\\ \beta=\gamma =1} \Rightarrow \alpha\gt \beta=\gamma,故選\bbox[red, 2pt]{(A)}$$
解答:$$f(x)=2x^2+x+3 =ax(x-1)+bx(x-3)+c(x-1)(x-3) \\ \Rightarrow \cases{f(0)=3=3c\\ f(1)=6=-2b\\f(3)=24=6a} \Rightarrow \cases{a=4\\ b=-3\\ c=1} \Rightarrow a+b+c=2,故選\bbox[red, 2pt]{(B)}$$
解答:$$(0,b)是兩圖形的交點,只有(C)符合要求;是,故選\bbox[red, 2pt]{(C)}$$
解答:$$原數據x_i並沒有上下界,因此T分數不一定介於0~100之間,其他皆正確,故選\bbox[red, 2pt]{(C)}$$
解答:$$甲、乙、戊長度皆是3,只是中心位置不同,故選\bbox[red, 2pt]{(D)}$$
解答:$$將資料轉換成相同的z分數才能比較高低,故選\bbox[red, 2pt]{(C)}$$
解答:$$f(x)為偶函數\Rightarrow f(3)=f(-3)=4,故選\bbox[red, 2pt]{(C)}$$
解答:$$f(x)={x(2x-1) (13x+2)^4 \over \sqrt{27x+9}} \Rightarrow f'(x)={(2x-1) (13x+2)^4 \over \sqrt{27x+9}} +xg(x) \Rightarrow f'(0)={-2^4\over \sqrt 9}=-{16\over 3}\\,故選\bbox[red, 2pt]{(A)}$$
解答:$$\lim_{n\to \infty} \left({2n^2+1\over n}-{2n^2+n+2 \over n+2} \right) =\lim_{n\to \infty} \left({(2n^2+1)(n+2)-n(2n^2 +n+2)\over n(n+2)} \right) \\=\lim_{n\to \infty}{3n^2\over n^2} =3 (只考慮高次項係數),故選\bbox[red, 2pt]{(D)}$$
解答:$$直線L通過(9,5)及(3,1) \Rightarrow y=f(x)={2\over 3}x-1 \Rightarrow f'(x)={2\over 3} \Rightarrow \lim_{h\to 0} {f(3+h)-f(3)\over h} ={2\over 3}\\,故選\bbox[red, 2pt]{(B)}$$
解答:$$\int_{-1}^3 |2x-1|\,dx = \int_{-1}^{1/2} (1-2x)\,dx + \int_{1/2}^3 (2x-1)\,dx = \left. \left[x-x^2 \right] \right|_{-1}^{1/2} +\left. \left[ x^2-x\right] \right|_{1/2}^{3} \\={9\over 4}+{25\over 4}={17\over 2},故選\bbox[red, 2pt]{(B)}$$
解答:$$\lim_{x\to 0}(x-{1\over x})\sin x =\lim_{x\to 0}{\sin x\over {x\over x^2-1}} =\lim_{x\to 0}{(\sin x)' \over ({x\over x^2-1})'} =\lim_{x\to 0}{\cos x\over {1\over x^2-1}-{2x^2 \over (x^2-1)^2}} ={1\over -1+0}=-1\\,故選\bbox[red, 2pt]{(A)}$$
解答:$$\cases{f_1(x)=x^{2/3} \Rightarrow f_1'(x)={2\over 3}\cdot {1\over x^{1/3}} \Rightarrow f_1'(0)不存在 \\f_2(x)=|x^2-2| \Rightarrow x=\pm \sqrt 2時,f_2(x)不可微} ,故選\bbox[red, 2pt]{(D)}$$
解答:$$\cases{x+2y+(3-a)=0 \cdots(1)\\ x+(2-a)y+3=0 \cdots(2)\\ (1-a)x+2y+3=0\cdots (3)},由(1)及(2)可得\cases{x=a-5\\ y=1} 代入(3) \Rightarrow (1-a)(a-5)+5=0\\ \Rightarrow a^2-6a=0 \Rightarrow a=0,6,故選\bbox[red, 2pt]{(B)}$$

解答:$$\lim_{x\to 6}f(x)=\pm 1 \Rightarrow 不存在,故選\bbox[red, 2pt]{(C)}$$

解答:$$f(x)={x-5\over x^2-9x+20} ={x-5\over (x-4)(x-5)},故選\bbox[red, 2pt]{(D)}$$

解答:$$f(x)=\left( {1\over x}+1\right)(2x+1) \Rightarrow f'(x)= \left( -{1\over x^2}\right)(2x+1) +\left( {1\over x}+1\right)\cdot 2 =-{2\over x}-{1\over x^2}+{2\over x}+2 \\=2-{1\over x^2},故選\bbox[red, 2pt]{(D)}$$

解答:$$\lim_{x\to 4} {\sqrt{x+5}-3\over x-4} =\lim_{x\to 4} {(\sqrt{x+5}-3)' \over (x-4)'} = \lim_{x\to 4} {{1\over 2\sqrt{x+5}}\over 1} = {1\over 6},故選\bbox[red, 2pt]{(B)}$$
解答:$$f(x)=x^3-9x^2+27x-27 \Rightarrow f'(x)=3x^2-18x+27 \Rightarrow f''(x)=6x-18 =0 \Rightarrow x=3\\,故選\bbox[red, 2pt]{(C)}$$

解答:$$(A)\bigcirc: \text{rref}\left(\left[\begin{matrix}1 & 0 & -1\\2 & 5 & 1\\0 & -4 & 3\end{matrix}\right] \right) =\left[\begin{matrix}1 & 0 & 0\\0 & 1 & 0\\0 & 0 & 1\end{matrix}\right] =I_3 \Rightarrow \text{ rank }=3\\ (B)\times: \text{rref}\left(\left[\begin{matrix}2 & -4 & 1\\0 & 3 & -1\\6 & 0 & -1\end{matrix}\right] \right) =\left[\begin{matrix}1 & 0 & - \frac{1}{6}\\0 & 1 & - \frac{1}{3}\\0 & 0 & 0\end{matrix}\right] \Rightarrow \text{ rank }=2\\ (C)\bigcirc:\text{rref}\left( \left[\begin{matrix}1 & 2 & -1\\1 & 0 & 2\\2 & 1 & 1\end{matrix}\right] \right)=I_3 \Rightarrow \text{ rank }=3 \\ (D)\bigcirc:\text{rref}\left( \left[\begin{matrix}-1 & 3 & 1\\2 & -4 & -3\\-3 & 8 & 2\end{matrix}\right]\right) =I_3 \Rightarrow \text{ rank }=3\\,故選\bbox[red, 2pt]{(B)}$$

解答:$$(C)\times: \{\vec v_1=(1,0),\vec v_2=(0,1), \vec v_3=(2,0)\} ,由於\vec v_3=2\vec v_1,為一線性相依集,\\\qquad 但其子集\{\vec v_1,\vec v_2\} 為線性獨立集\\,故選\bbox[red, 2pt]{(C)}$$

解答:$$A= \left[\begin{matrix}1 & 1 & 0\\2 & 1 & 1\\1 & 1 & 1\end{matrix}\right] \Rightarrow rref(A)= \left[\begin{matrix}1 & 0 & 0\\0 & 1 & 0\\0 & 0 & 1\end{matrix}\right] =I_3 \Rightarrow rank(A)=3,故選\bbox[red, 2pt]{(A)}$$

解答:$$\begin{vmatrix}2i & 3 \\4 & 6i \end{vmatrix} =-12-12= -24,故選\bbox[red, 2pt]{(C)}$$

解答:$$4x^2-13x+7=0 \Rightarrow \cases{a_1=13/4\\ a_2=7/4} \Rightarrow a_1-a_2={6\over 4} ={3\over 2},故選\bbox[red, 2pt]{(D)}$$

解答:$$(B) \bigcirc: {-3\over 9} ={1\over -3}={7\over -21},故選\bbox[red, 2pt]{(B)}$$


解答:$${1\over n}+ {3\over n}+ {5\over n}+ {7\over n}+ {9\over n}+ {11\over n}+ {13\over n} ={49\over n} 為整數 \Rightarrow n=1,7,49,有三個,故選\bbox[red, 2pt]{(C)}$$

解答:$$(A)\times: \sqrt x 不是x的多項式\\ (B)\times: 3^{2x}不是x的多項式 \\(D)\times:{1\over x^2} 不是x的多項式\\,故選\bbox[red, 2pt]{(C)}$$

解答:$$xf(x)= (x-3)p(x) +6 \Rightarrow 3f(3)= 6 \Rightarrow f(3)=2,故選\bbox[red, 2pt]{(C)}$$
解答:$$\int_{-1}^3 |2x-1|\,dx = \int_{-1}^{1/2} (1-2x)\,dx + \int_{1/2}^3 (2x-1)\,dx = \left. \left[x-x^2 \right] \right|_{-1}^{1/2} +\left. \left[ x^2-x\right] \right|_{1/2}^{3} \\={9\over 4}+{25\over 4}={17\over 2},故選\bbox[red, 2pt]{(B)}$$
解答:$$\lim_{x\to 0}(x-{1\over x})\sin x =\lim_{x\to 0}{\sin x\over {x\over x^2-1}} =\lim_{x\to 0}{(\sin x)' \over ({x\over x^2-1})'} =\lim_{x\to 0}{\cos x\over {1\over x^2-1}-{2x^2 \over (x^2-1)^2}} ={1\over -1+0}=-1\\,故選\bbox[red, 2pt]{(A)}$$
解答:$$\cases{f_1(x)=x^{2/3} \Rightarrow f_1'(x)={2\over 3}\cdot {1\over x^{1/3}} \Rightarrow f_1'(0)不存在 \\f_2(x)=|x^2-2| \Rightarrow x=\pm \sqrt 2時,f_2(x)不可微} ,故選\bbox[red, 2pt]{(D)}$$
解答:$$(B)\times:若\cases{A=\begin{bmatrix}1 & 0 \\0 & 0 \end{bmatrix}\\[1ex] B=\begin{bmatrix}0 & 1 \\0 & 0 \end{bmatrix}} \Rightarrow \cases{AB=\begin{bmatrix}0 & 1 \\0 & 0 \end{bmatrix} \\[1ex]BA=\begin{bmatrix}0 & 0 \\0 & 0 \end{bmatrix}} \Rightarrow AB\ne BA\\ (C)\times: (A+B)^2=A^2+AB+ BA+B^2, AB不一定等於BA\\ (D)\times: 若C=0 \Rightarrow AC=BC並不能代表A=B\\,故選\bbox[red, 2pt]{(A)}$$
解答:$$\cases{x+2y+(3-a)=0 \cdots(1)\\ x+(2-a)y+3=0 \cdots(2)\\ (1-a)x+2y+3=0\cdots (3)},由(1)及(2)可得\cases{x=a-5\\ y=1} 代入(3) \Rightarrow (1-a)(a-5)+5=0\\ \Rightarrow a^2-6a=0 \Rightarrow a=0,6,故選\bbox[red, 2pt]{(B)}$$

解答:$$\lim_{x\to 6}f(x)=\pm 1 \Rightarrow 不存在,故選\bbox[red, 2pt]{(C)}$$

解答:$$f(x)={x-5\over x^2-9x+20} ={x-5\over (x-4)(x-5)},故選\bbox[red, 2pt]{(D)}$$

解答:$$f(x)=\left( {1\over x}+1\right)(2x+1) \Rightarrow f'(x)= \left( -{1\over x^2}\right)(2x+1) +\left( {1\over x}+1\right)\cdot 2 =-{2\over x}-{1\over x^2}+{2\over x}+2 \\=2-{1\over x^2},故選\bbox[red, 2pt]{(D)}$$

解答:$$\lim_{x\to 4} {\sqrt{x+5}-3\over x-4} =\lim_{x\to 4} {(\sqrt{x+5}-3)' \over (x-4)'} = \lim_{x\to 4} {{1\over 2\sqrt{x+5}}\over 1} = {1\over 6},故選\bbox[red, 2pt]{(B)}$$

解答:$$f(x)=x^3-9x^2+27x-27 \Rightarrow f'(x)=3x^2-18x+27 \Rightarrow f''(x)=6x-18 =0 \Rightarrow x=3\\,故選\bbox[red, 2pt]{(C)}$$

解答:$$(A)\bigcirc: \text{rref}\left(\left[\begin{matrix}1 & 0 & -1\\2 & 5 & 1\\0 & -4 & 3\end{matrix}\right] \right) =\left[\begin{matrix}1 & 0 & 0\\0 & 1 & 0\\0 & 0 & 1\end{matrix}\right] =I_3 \Rightarrow \text{ rank }=3\\ (B)\times: \text{rref}\left(\left[\begin{matrix}2 & -4 & 1\\0 & 3 & -1\\6 & 0 & -1\end{matrix}\right] \right) =\left[\begin{matrix}1 & 0 & - \frac{1}{6}\\0 & 1 & - \frac{1}{3}\\0 & 0 & 0\end{matrix}\right] \Rightarrow \text{ rank }=2\\ (C)\bigcirc:\text{rref}\left( \left[\begin{matrix}1 & 2 & -1\\1 & 0 & 2\\2 & 1 & 1\end{matrix}\right] \right)=I_3 \Rightarrow \text{ rank }=3 \\ (D)\bigcirc:\text{rref}\left( \left[\begin{matrix}-1 & 3 & 1\\2 & -4 & -3\\-3 & 8 & 2\end{matrix}\right]\right) =I_3 \Rightarrow \text{ rank }=3\\,故選\bbox[red, 2pt]{(B)}$$

解答:$$(C)\times: \{\vec v_1=(1,0),\vec v_2=(0,1), \vec v_3=(2,0)\} ,由於\vec v_3=2\vec v_1,為一線性相依集,\\\qquad 但其子集\{\vec v_1,\vec v_2\} 為線性獨立集\\,故選\bbox[red, 2pt]{(C)}$$

解答:$$A= \left[\begin{matrix}1 & 1 & 0\\2 & 1 & 1\\1 & 1 & 1\end{matrix}\right] \Rightarrow rref(A)= \left[\begin{matrix}1 & 0 & 0\\0 & 1 & 0\\0 & 0 & 1\end{matrix}\right] =I_3 \Rightarrow rank(A)=3,故選\bbox[red, 2pt]{(A)}$$

解答:$$\begin{vmatrix}2i & 3 \\4 & 6i \end{vmatrix} =-12-12= -24,故選\bbox[red, 2pt]{(C)}$$

解答:$$4x^2-13x+7=0 \Rightarrow \cases{a_1=13/4\\ a_2=7/4} \Rightarrow a_1-a_2={6\over 4} ={3\over 2},故選\bbox[red, 2pt]{(D)}$$

解答:$$(B) \bigcirc: {-3\over 9} ={1\over -3}={7\over -21},故選\bbox[red, 2pt]{(B)}$$
解答:$$2^x=5 \Rightarrow \log_2 2^x= \log_2 5 \Rightarrow x=\log_2 5,故選\bbox[red, 2pt]{(B)}$$
解答:$${|2+2-k| \over \sqrt 5} ={|4-k|\over \sqrt5} ={1\over \sqrt 5} \Rightarrow 4-k=\pm 1 \Rightarrow k=3,5,故選\bbox[red, 2pt]{(A)}$$
解答:$$(A) \times: x^2+y^2+z^2={3\over 2} \ne 1 \\ (B) \times: x^2+y^2+z^2=2 \ne 1 \\(C) \bigcirc: x^2+y^2+z^2= 1 \\(D) \times: x^2+y^2+z^2={5 \over 4} \ne 1 \\,故選\bbox[red, 2pt]{(C)}$$
解答:$$\cases{2的倍數有200/2=100個\\ 3的倍數有 \lfloor 200/3 \rfloor =66個\\ 5的倍數有 \lfloor 200/5 \rfloor =40個\\ 6的倍數有 \lfloor 200/6 \rfloor =33個\\ 10的倍數有 \lfloor 200/10 \rfloor =20個\\ 15的倍數有 \lfloor 200/15 \rfloor =13個\\ 30的倍數有 \lfloor 200/30 \rfloor =6個} \Rightarrow 100+66+40-33-20-13+6=146,故選\bbox[red, 2pt]{(B)}$$

解答:$$(A)\times: \sqrt x 不是x的多項式\\ (B)\times: 3^{2x}不是x的多項式 \\(D)\times:{1\over x^2} 不是x的多項式\\,故選\bbox[red, 2pt]{(C)}$$

解答:$$xf(x)= (x-3)p(x) +6 \Rightarrow 3f(3)= 6 \Rightarrow f(3)=2,故選\bbox[red, 2pt]{(C)}$$
解答:$$f(-1)=f(3)=f(5/2)=0 \Rightarrow -1,3,5/2為f(x)=0的根 \Rightarrow (x+1)(x-3)(2x-5)可整除f(x)\\,故選\bbox[red, 2pt]{(C)}$$

解答:$$\begin{array}{} 樣本& 次數& 報酬\\\hline 三正& 1& 15\\ 二正一反&3 & 8\\ 一正二反 & 3& 1\\ 三反& 1 & -6 \\\hline \end{array} \Rightarrow 期望值={1\over 8}(1\cdot 15+3\cdot 8+3\cdot 1-1\cdot 6) ={9\over 2},故選\bbox[red, 2pt]{(B)}$$

解答:$$a_n=2a_{n-1}+1=2(2a_{n-2}+1)+1=2^2 a_{n-2}+2+1 =2^3a_{n-3}+ 2^2+2+1 =\cdots\\=2^{n-1}a_1+2^{n-2}+2^{n-1}+ \cdots + 1=2^{n-1} +2^{n-2}+2^{n-1}+ \cdots + 1 =2^n-1,故選\bbox[red, 2pt]{(D)}$$

解答:$$a_2={2\over 1}a_1=2 \Rightarrow a_3={3\over 2}a_2=3 \Rightarrow a_4={4\over 3}a_3=4 \Rightarrow a_{50}=50,故選\bbox[red, 2pt]{(D)}$$

解答:$$A\cap B=\{-2, 4\} \Rightarrow a^2+a-4=-2 \Rightarrow a^2+a-2=0 \\\Rightarrow \cases{a=1 \Rightarrow B=\{-2,6,4\} \Rightarrow A\cap B=\{-2,4\}\\ a=-2 \Rightarrow B=\{-2,3,10\} \Rightarrow A\cap B=\{-2\}} \Rightarrow a=1,故選\bbox[red, 2pt]{(D)}$$
解答:$$(A)\bigcirc: \langle a_n\rangle 首項a_1,公差d \Rightarrow \langle 4a_n\rangle 首頁4a_1,公差4d,仍為等差數列\\,故選\bbox[red, 2pt]{(A)}$$

解答:$$著色部分=B\cap C去掉A=B\cap C\cap A',故選\bbox[red, 2pt]{(A)}$$
解答:$$五男任選一男有5種選法,再從四女中任選一女有4種選法,共5\times 4=20種選法,故選\bbox[red, 2pt]{(C)}$$

解答:$$5種面額有2^5=32種付法,扣除完全不支付,即32-1=31種,故選\bbox[red, 2pt]{(B)}$$

解答:$$\textbf{Case I }用了四種顏色:5\times 4\times 3\times 3=120 \\\textbf{Case II }用了三種顏色: \cases{B,D同色:5\times 4\times 3=60\\ A,C同色:5\times 4\times 3=60} \Rightarrow 合計120\\\textbf{Case III }用了二種顏色:A,C同色且B,D同色:5\times 4=20 \\ 三種情況共有120+120+20=260種塗法,故選\bbox[red, 2pt]{(D)}$$
解答:$$個位數只能是5,只有一種選擇;十位數字及百位數字各有5種選擇,因此總共有1\times 5\times 5=5^2種\\,故選\bbox[red, 2pt]{(B)}$$解答:$$與A互斥的事件,就是出現2或4,共有2^2=4個事件,故選\bbox[red, 2pt]{(A)}$$

解答:$$把小華座位拿走,剩下35人任排有35!排法;原來36人有36!排法,因此機率為{35!\over 36!} ={1\over 36}\\,故選\bbox[red, 2pt]{(A)}$$
解答:$$\cases{沒有抽中紅球機率={C^3_3/C^8_3} \\抽中1紅球機率={C^5_1C^3_2/C^8_3} } \Rightarrow 抽中至少兩紅球機率=1-{C^3_3\over C^8_3} -{C^5_1C^3_2\over C^8_3} =1-{2\over 7} ={5\over 7}\\,故選\bbox[red, 2pt]{(D)}$$
解答:$$兩次都沒出現2點的機率={5\over 6}\times {5\over 6}={25\over 36} \Rightarrow 至少出現一次2點的機率=1-{25\over 36} ={11\over 36}\\,故選\bbox[red, 2pt]{(A)}$$
解答:$$(1,2), (1,5), (2,1),(2,4),(3,3),(3,6),(4,2),(4,5),(5,1),(5,4),(6,3),(6,6)\\ 共12種,機率為{12\over 36},故選\bbox[red, 2pt]{(C)}$$
解答:$${4\over 5+4}={4\over 9},故選\bbox[red, 2pt]{(A)}$$
解答:$$S=p+2p^2+ 3p^3+ \cdots \Rightarrow pS=p^2+2p^3+3p^4 +\cdots \Rightarrow (1-p)S=p+p^2 +p^3+\cdots \\ \Rightarrow S={p\cdot {1\over 1-p} \over 1-p} ={p\over (1-p)^2},故選\bbox[red, 2pt]{(B)}$$
解答:$$故選\bbox[red, 2pt]{(C)}$$
解答:$$ 選\bbox[red, 2pt]{(D)}$$
解答:$${陽性且是患著\over 陽性} ={10 \% \times 0.8 \over 10\% \times 0.8+ 90\% \times 0.2} = 0.307,故選\bbox[red, 2pt]{(C)}$$

解答:$$\cases{A\cap B=\{1\} \\ A\cap B\cap C=\{ 1\}} \Rightarrow P(A\cap B) =P(A\cap B\cap C)={1\over 4},故選\bbox[red, 2pt]{(A)}$$
解答:$$\cases{第一回合就贏:{1\over 6}\\ 第二回合才贏:{5\over 6}\times{1\over 2} \times{1\over 6}\\ 第三回合才贏:({5\over 6}\times{1\over 2})^2 \times{1\over 6} \\ \cdots}\Rightarrow 合計={1\over 6}\left( 1+ {5\over 12} +({5\over 12})^2 +\cdots\right) ={1\over 6}\cdot {1\over 1-{5\over 12}} ={2\over 7}\\,故選\bbox[red, 2pt]{(B)}$$

解答:$$1.2^n=2 \Rightarrow n=4,故選\bbox[red, 2pt]{(B)}$$
解答:$$(A) \times:A= \begin{bmatrix} 1& -1\\ 1& 1\end{bmatrix} \Rightarrow A^2 =\begin{bmatrix} 0& -2\\2& 0\end{bmatrix} \Rightarrow -2 \lt 0\\ (B)\times: 由上例可知: 2 \gt 0 \\(C) \bigcirc: \det(A^2)=\det(AA) =\det A\det A \ge 0 \\(D) \times: A= \begin{bmatrix} 0& 0\\ 1& 0\end{bmatrix} \Rightarrow A^2= \begin{bmatrix} 0& 0\\ 0& 0\end{bmatrix} \Rightarrow A有兩個不同的特徵向量,但A^2沒有,故選\bbox[red, 2pt]{(C)}$$
解答:$$\cases{f(x,y)=xy\\ g(x,y)=x^2+y^2-2} \Rightarrow \cases{f_x=\lambda g_x\\ f_y= \lambda g_y\\ g=0} \Rightarrow \cases{y=2\lambda x\\ x=2\lambda y} \Rightarrow {y\over x}={x\over y} \Rightarrow x^2=y^2\\ \Rightarrow \cases{x=y \Rightarrow f(x,x)=x^2\\ x=-y \Rightarrow f(x,-x)=-x^2} \Rightarrow \cases{最大值在x=y上\\ 最小值在x=-y上},故選\bbox[red, 2pt]{(C)}$$
解答:$$A=\begin{bmatrix}2 & 1+i \\1-i & -2 \end{bmatrix} \Rightarrow \det(A-\lambda I)=\lambda^2-6=0 \Rightarrow \lambda=\pm \sqrt 6,故選\bbox[red, 2pt]{(B)}$$
解答:$$(0,0)不在陰影區,因此(B)及(C)不正確;又(5,1)在陰影區,只有(A)正確,故選\bbox[red, 2pt]{(A)}$$
解答:$$此題相當求兩圖形\cases{y=2^x\\ y=x^2+1}的交點數,顯然有兩個焦點(0,1)及(1,2),\\又O(2^x)\gt O(x^2) 因此在x\gt 1還有一個交點,故選\bbox[red, 2pt]{(D)}$$
解答:$$\cases{(\sqrt 3)^6= 27\\ (\sqrt[3] 4)^6 =16\\ (\sqrt[6]{18})^6 =18} \Rightarrow \sqrt 3\gt \sqrt[6]{18} \gt \sqrt[3] 4,故選\bbox[red, 2pt]{(B)}$$
解答:
$$假設正立方體邊長為1,如上圖;\triangle ACQ, \triangle ACS ,\triangle BDP, \triangle BDR, \triangle QSC, \triangle QSA, \triangle PRB, \triangle PRD\\ 皆為邊長\sqrt 2的正三角形,共8個,故選\bbox[red, 2pt]{(A)}$$
解答:$${(2+2i)^8 \over (-1+\sqrt 3i)^{12}} ={2^{12}({1\over \sqrt 2}+{1\over \sqrt 2}i)^8 \over 2^{12}(-{1\over 2}+{\sqrt 3\over 2}i)^{12}} ={(e^{\pi i/4})^8 \over (e^{2\pi i/3})^{12}} ={e^{2\pi i} \over e^{8\pi i}} =1,故選\bbox[red, 2pt]{(A)}$$
解答:$$\vec a\bot \vec b \Rightarrow \vec a\cdot \vec b=0 \Rightarrow \cases{2\vec x-3\vec y=\vec a\\ 3\vec x+\vec y=\vec b} \Rightarrow \cases{\vec x={1\over 11}\vec a+{3\over 11}\vec b\\ \vec y=-{3\over 11}\vec a+{2\over 11}\vec b} \Rightarrow \cases{|\vec x|=\sqrt{10}/11\\ |\vec y|=\sqrt{13}/11\\ \vec x\cdot \vec y=3/121} \\ \Rightarrow \cos \theta ={\vec x\cdot \vec y \over |\vec x||\vec y|} ={3\over \sqrt{130}},故選\bbox[red, 2pt]{(B)}$$
解答:$$(A)\bigcirc: 66^n除以13的餘數皆為1 \Rightarrow 66^{111}-1是13的倍數\\ (B)\times: 2^n 除以13的餘數為2,4 ,8 ,3,6,12, 11, 9, 5, 10, 7, 1,\dots,循環數為12 \Rightarrow 998=12\times 83+2 \\\qquad \Rightarrow 2^{998} =4 \text{ mod }13= 4\Rightarrow 2^{998}+8 = 12 \text{ mod }13 \Rightarrow 不是13的倍數 \\(C) \bigcirc: 68^n 除以13的餘數為3,9,1,3,9,1,\dots,循環數為3 \Rightarrow 33=3\times 11 \Rightarrow 68^{33} = 1 \text{ mod }13 \\\qquad\Rightarrow 68^{33}-1是13的倍數 \\(D)\bigcirc: 18^n除以13的餘數為5,12,8,1,5,12,\dots,循環數為4 \Rightarrow 50=4\times 12+2 \\\qquad \Rightarrow 18^{50} = 12 \text{ mod }13 \Rightarrow 18^{50} +1是13的倍數\\,故選\bbox[red, 2pt]{(B)}$$
解答:$$\cases{三相同,只有bbb \Rightarrow 1\\ 2同1異\Rightarrow C^4_1C^3_1\times 3=36\\三不同\Rightarrow C^4_3\times 3!=24} \Rightarrow 合計1+36+24=61,故選\bbox[red, 2pt]{(D)}$$
解答:$$\cases{個位數只是1,3,5,7有4種可能\\ 百位數不能4也不能與個位數相同,有5種可能\\ 十位數剩下5種選擇\\ 千位數剩下4種選擇} \Rightarrow 共有4\times 5\times 5\times 4=400種,故選\bbox[red, 2pt]{(C)}$$
解答:$$3f(x)+f({1\over x})=x \Rightarrow \cases{3f(2)+f({1\over 2})=2\\ 3f({1\over 2})+f(2)={1\over 2}} \Rightarrow f(2)={11\over 26}\\ 同理\cases{3f(3)+f({1\over 3})= 3\\ 3f({1\over 3})+f(3)={1\over 3}} \Rightarrow f(3)={26\over 24} \\ 因此24f(3)-16f(2)=26-11=15,故選\bbox[red, 2pt]{(D)}$$
解答:$$P在4x^2-y^2=4上 \Rightarrow P(\sqrt{4+a^2\over 4},a) \Rightarrow \overline{AP} =\sqrt{{4+a^2\over 4}+ (a-3)^2)} =\sqrt{{5\over 4}a^2-6a+10} \\ 令f(a) ={5\over 4}a^2-6a+10 \Rightarrow f'(a)=0 \Rightarrow a= {12\over 5} \Rightarrow f({12\over 5}) ={14\over 5}=2.8 \Rightarrow \overline{AP}= \sqrt{2.8},故選\bbox[red, 2pt]{(D)}$$
解答:$$\overrightarrow{AP} ={3\over 2}\overrightarrow{AQ} ={3\over 2}(\overrightarrow{AB} +\overrightarrow{BQ}) ={3\over 2}(\overrightarrow{AB} + {3\over 2}\overrightarrow{BR}) ={3\over 2}\overrightarrow{AB} + {9 \over 4}\overrightarrow{BR} ={3\over 2}\overrightarrow{AB} + {9 \over 4}(\overrightarrow{BC} +\overrightarrow{CR}) \\ ={3\over 2}\overrightarrow{AB} + {9 \over 4}(\overrightarrow{BA} +\overrightarrow{AC} + {4\over 3} \overrightarrow{CP}) =-{3\over 4} \overrightarrow{AB} +{9\over 4}\overrightarrow{AC} +3(\overrightarrow{CA}+ \overrightarrow{AP}) =-{3\over 4} \overrightarrow{AB} -{3\over 4} \overrightarrow{AC} +3 \overrightarrow{AP} \\ \Rightarrow 2\overrightarrow{AP} ={3\over 4} \overrightarrow{AB} +{3\over 4} \overrightarrow{AC} \Rightarrow \overrightarrow{AP} ={3\over 8} \overrightarrow{AB} +{3\over 8} \overrightarrow{AC} \Rightarrow x+y={3\over 8}+{3\over 8}={3\over 4},故選\bbox[red, 2pt]{(C)}$$
解答:$$a=\sqrt{14+\sqrt{21}} \Rightarrow \sqrt{14+\sqrt{16}}\lt a\lt \sqrt{14+\sqrt{25}} \Rightarrow 4\lt\sqrt{18} \lt a\lt \sqrt{19}\lt 5 \\ \Rightarrow 4\lt a\lt 5,故選\bbox[red, 2pt]{(B)}$$
解答:$$\cases{\lim_{x\to 1}{f(x)\over x-1}=-3\\ \lim_{x\to 2}{f(x)\over x-2}=5 } \Rightarrow \cases{f(x)=(x-1)g(x) 且g(1)=-3\\ f(x)=(x-2)h(x)且h(2)=5} \\ \Rightarrow f(x)=(x-1)(x-2)(ax+b) \Rightarrow \cases{-(a+b)=-3\\ 2a+b=5} \Rightarrow \cases{a=2\\b=1} \\ \Rightarrow f(x)=(x-1)(x-2)(2x+b) \Rightarrow f(0)=2b=2,故選\bbox[red, 2pt]{(A)}$$
解答:$$\cases{(\log 3)x+ \log y=\log 2\\ (\log 9)x+3\log y=\log 16} \Rightarrow \cases{\log (3^x\cdot y)=\log 2\\ \log (9^x\cdot y^3) =\log 16} \Rightarrow \cases{y3^x=2 \Rightarrow y=2/3^x\\ y^33^{2x}=16} \\ \Rightarrow ({2\over 3^x})^3 \cdot 3^{2x} ={8\over 3^x}=16 \Rightarrow 3^x={1\over 2} \Rightarrow y=2/3^x=4 \Rightarrow 3^a+b={1\over 2}+4={9\over 2},故選\bbox[red, 2pt]{(C)}$$
解答:$$f(x)=x^{10}+2x+1 \Rightarrow f'(x)=10x^9+2 \Rightarrow f'(-1)=-8 \\ \Rightarrow \lim_{h\to 0}{f(2h-1)-f(-1)\over h} = \lim_{h\to 0}{(f(2h-1)-f(-1))'\over (h)'} = \lim_{h\to 0}{2f'(2h-1) \over 1} = 2f'(-1)= -16\\,故選\bbox[red, 2pt]{(A)}$$
解答:$$f(x)=(x+1)p(x)-1= (x-2)q(x)+5=(x^2-x-2)r(x)+ax+b \\\quad =(x-2)(x+1)r(x)+ax+b \Rightarrow \cases{f(-1)=-1=-a+b\\ f(2)=5=2a+b} \Rightarrow \cases{a=2\\ b=1} \\ \Rightarrow 餘式為2x+1,故選\bbox[red, 2pt]{(B)}$$
解答:$$\cos 60^\circ ={\vec a\cdot \vec b\over |\vec a||\vec b|} \Rightarrow \vec a\cdot \vec b={1\over 2} \cdot 1\cdot 3={3\over 2} \\ \Rightarrow (2\vec a-\vec b)\cdot (2\vec a-\vec b) =4|\vec a|^2-4\vec a\cdot \vec b+|\vec b|^2 = 4-6+9=7 \Rightarrow |2\vec a-\vec b|=\sqrt 7,故選\bbox[red, 2pt]{(D)}$$
解答:$$\cases{\log_{(5-x) } (-x^2+10x-5)\\ \log_{(5-x)}(2x+10)} \Rightarrow \cases{5-x\gt 0\\ -x^2+10x-5\gt 0\\ 2x+10\gt 0} \Rightarrow \cases{5\gt x\\ 5-2\sqrt 5 \lt x\lt 5+2\sqrt 5 \\ x\gt -5} \\\Rightarrow 5-2\sqrt 5\lt x\lt 5 \cdots(1);\; 又\cases{5-x\gt 1 \Rightarrow -x^2+10x-5 \lt 2x+10 \Rightarrow x\lt 3\cdots(2)\\ 5-x\lt 1 \Rightarrow -x^2+10x-5 \gt 2x+10 \Rightarrow 4\lt x\lt 5 \cdots(3)} \\ \Rightarrow \cases{ (1)\cap (2) \Rightarrow 5-2\sqrt 5\lt x\lt 3\\ (1)\cap (3) \Rightarrow 4\lt x\lt 5 },故選\bbox[red, 2pt]{(D)}$$
解答:$$\begin{vmatrix} -1& 2& -1\\ 1& 1& 2\\ 0 & 1& 3\end{vmatrix} =-3-1+0-0-6+2=-8,故選\bbox[red, 2pt]{(B)}$$
解答:$$\cases{A(1,-1,1) \\B(-3,2,1) \\C(5,-4,3)} \Rightarrow \cases{\vec u= \overrightarrow{AB}=(-4,3,0) \\ \vec v= \overrightarrow{AC} =(4,-3,2)} \Rightarrow \vec n=\vec u\times \vec v=(6,8,0) \\ \Rightarrow S_{\triangle ABC} ={1\over 2}\Vert \vec n\Vert ={1\over 2} \sqrt{6^2+8^2} =5,故選\bbox[red, 2pt]{(C)}$$
解答:$$\#(A\cup B\cup C)= \#(A)+ \#(B)+ \#(C)- \#(A\cap B)-\#(B\cap C)- \#(C\cap A)+ \#(A\cap B\cap C) \\ =28+29+25-10-11-12+3=52,故選\bbox[red, 2pt]{(B)}$$
解答:$$z+z^{-1}= -\sqrt 3 \Rightarrow z^2+\sqrt 3z+1=0 \Rightarrow z=-{\sqrt 3\over 2}+{1\over 2}i =e^{5\pi i/6} \\ \Rightarrow z^{10} +z^{-10} =e^{50\pi i/6}+ e^{-50\pi /6} = 2\cos {50\over 6}\pi =2\cos {\pi\over 3} =1,故選\bbox[red, 2pt]{(A)}$$
解答:$$\lim_{x\to \infty} {x-\sin x\over x} =\lim_{x\to \infty} \left(1-{\sin x\over x}\right) = 1-0=1,故選\bbox[red, 2pt]{(A)}$$
解答:$$\int_0^3 x[x]\,dx = \int_0^1 0\,dx +\int_1^2 x \,dx +\int_2^3 2x\,dx = 0+{3\over 2}+4={11\over 2},故選\bbox[red, 2pt]{(D)}$$
解答:$$x^3+y^3-9xy=0 \Rightarrow 3x^2+3y^2y'-9y-9xy'=0 \Rightarrow y'={9y-3x^2\over 3y^2-9x} \\ \Rightarrow y'(2,4)={36-12\over 48-18} ={24\over 30}={4\over 5},故選\bbox[red, 2pt]{(D)}$$
解答:$$A為5\times 3 \Rightarrow A^T=3\times 5 \Rightarrow B為5\times n,又C為7\times 4 \Rightarrow n=7 \Rightarrow B為5\times 7,故選\bbox[red, 2pt]{(A)}$$
解答:$$\cases{\tan \alpha +\tan \beta=-{b\over a} \\ \tan \alpha \tan \beta= {c\over a}} \Rightarrow \tan(\alpha+\beta) ={\tan \alpha+ \tan \beta\over 1-\tan \alpha \tan \beta} ={-b/a\over 1- c/a} =-{b\over a-c }\\ \Rightarrow \cot(\alpha+\beta) ={c-a\over b},故選\bbox[red, 2pt]{(D)}$$
解答:$$\left(x+{1\over x} \right)^2 =x^2+{1\over x^2}+2 \Rightarrow 2\left(x^2+{1\over x^2} \right)-9\left(x+{1\over x} \right) +14 =2\left(x+{1\over x} \right)^2-9\left(x+{1\over x} \right) +10 \\=\left( 2\left(x+{1\over x} \right)-5\right) \left( \left(x+{1\over x} \right)-2\right)=0 \Rightarrow\cases{x+{1\over x}={5\over 2} \\x+{1\over x}=2} \Rightarrow \cases{2x^2-5x+2=0\\ x^2-2x+1=0} \\ \Rightarrow \cases{(2x-1)(x-2)=0\\ (x-1)^2=0} \Rightarrow x={1\over 2},1,2,故選\bbox[red, 2pt]{(C)}$$
解答:$$\lim_{x\to 0} {1-\cos x\over x^2} =\lim_{x\to 0} {(1-\cos x)'\over (x^2)'} = \lim_{x\to 0} { \sin x\over 2x} = \lim_{x\to 0} { (\sin x)'\over (2x)'} = \lim_{x\to 0} { \cos x\over 2} ={1\over 2},故選\bbox[red, 2pt]{(B)}$$
解答:$$4x^3-24x^2+23x+18=0 \Rightarrow \cases{三根之和=6\\ 三根之積=-9/2},故選\bbox[red, 2pt]{(B)}$$
解答:$$f(x)=(x+2)(x+5)^2 \Rightarrow f'(x)=(x+5)^2+2(x+2)(x+5) =(x+5)(3x+ 9) \\ \Rightarrow f''(x)=3x+9+3x+15 =6x+24\\ f''(x)=0 \Rightarrow x=-4 \Rightarrow 反曲點(-4,f(-4)) =(-4,-2),故選\bbox[red, 2pt]{(C)}$$
解答:$$\vec a\bot \vec b \Rightarrow \vec a\cdot \vec b=0 \Rightarrow \cases{2\vec x-3\vec y=\vec a\\ 3\vec x+\vec y=\vec b} \Rightarrow \cases{\vec x={1\over 11}\vec a+{3\over 11}\vec b\\ \vec y=-{3\over 11}\vec a+{2\over 11}\vec b} \Rightarrow \cases{|\vec x|=\sqrt{10}/11\\ |\vec y|=\sqrt{13}/11\\ \vec x\cdot \vec y=3/121} \\ \Rightarrow \cos \theta ={\vec x\cdot \vec y \over |\vec x||\vec y|} ={3\over \sqrt{130}},故選\bbox[red, 2pt]{(B)}$$
解答:$$(A)\bigcirc: 66^n除以13的餘數皆為1 \Rightarrow 66^{111}-1是13的倍數\\ (B)\times: 2^n 除以13的餘數為2,4 ,8 ,3,6,12, 11, 9, 5, 10, 7, 1,\dots,循環數為12 \Rightarrow 998=12\times 83+2 \\\qquad \Rightarrow 2^{998} =4 \text{ mod }13= 4\Rightarrow 2^{998}+8 = 12 \text{ mod }13 \Rightarrow 不是13的倍數 \\(C) \bigcirc: 68^n 除以13的餘數為3,9,1,3,9,1,\dots,循環數為3 \Rightarrow 33=3\times 11 \Rightarrow 68^{33} = 1 \text{ mod }13 \\\qquad\Rightarrow 68^{33}-1是13的倍數 \\(D)\bigcirc: 18^n除以13的餘數為5,12,8,1,5,12,\dots,循環數為4 \Rightarrow 50=4\times 12+2 \\\qquad \Rightarrow 18^{50} = 12 \text{ mod }13 \Rightarrow 18^{50} +1是13的倍數\\,故選\bbox[red, 2pt]{(B)}$$
解答:$$\cases{三相同,只有bbb \Rightarrow 1\\ 2同1異\Rightarrow C^4_1C^3_1\times 3=36\\三不同\Rightarrow C^4_3\times 3!=24} \Rightarrow 合計1+36+24=61,故選\bbox[red, 2pt]{(D)}$$
解答:$$\cases{個位數只是1,3,5,7有4種可能\\ 百位數不能4也不能與個位數相同,有5種可能\\ 十位數剩下5種選擇\\ 千位數剩下4種選擇} \Rightarrow 共有4\times 5\times 5\times 4=400種,故選\bbox[red, 2pt]{(C)}$$
解答:$$3f(x)+f({1\over x})=x \Rightarrow \cases{3f(2)+f({1\over 2})=2\\ 3f({1\over 2})+f(2)={1\over 2}} \Rightarrow f(2)={11\over 26}\\ 同理\cases{3f(3)+f({1\over 3})= 3\\ 3f({1\over 3})+f(3)={1\over 3}} \Rightarrow f(3)={26\over 24} \\ 因此24f(3)-16f(2)=26-11=15,故選\bbox[red, 2pt]{(D)}$$
解答:$$P在4x^2-y^2=4上 \Rightarrow P(\sqrt{4+a^2\over 4},a) \Rightarrow \overline{AP} =\sqrt{{4+a^2\over 4}+ (a-3)^2)} =\sqrt{{5\over 4}a^2-6a+10} \\ 令f(a) ={5\over 4}a^2-6a+10 \Rightarrow f'(a)=0 \Rightarrow a= {12\over 5} \Rightarrow f({12\over 5}) ={14\over 5}=2.8 \Rightarrow \overline{AP}= \sqrt{2.8},故選\bbox[red, 2pt]{(D)}$$
解答:$$\overrightarrow{AP} ={3\over 2}\overrightarrow{AQ} ={3\over 2}(\overrightarrow{AB} +\overrightarrow{BQ}) ={3\over 2}(\overrightarrow{AB} + {3\over 2}\overrightarrow{BR}) ={3\over 2}\overrightarrow{AB} + {9 \over 4}\overrightarrow{BR} ={3\over 2}\overrightarrow{AB} + {9 \over 4}(\overrightarrow{BC} +\overrightarrow{CR}) \\ ={3\over 2}\overrightarrow{AB} + {9 \over 4}(\overrightarrow{BA} +\overrightarrow{AC} + {4\over 3} \overrightarrow{CP}) =-{3\over 4} \overrightarrow{AB} +{9\over 4}\overrightarrow{AC} +3(\overrightarrow{CA}+ \overrightarrow{AP}) =-{3\over 4} \overrightarrow{AB} -{3\over 4} \overrightarrow{AC} +3 \overrightarrow{AP} \\ \Rightarrow 2\overrightarrow{AP} ={3\over 4} \overrightarrow{AB} +{3\over 4} \overrightarrow{AC} \Rightarrow \overrightarrow{AP} ={3\over 8} \overrightarrow{AB} +{3\over 8} \overrightarrow{AC} \Rightarrow x+y={3\over 8}+{3\over 8}={3\over 4},故選\bbox[red, 2pt]{(C)}$$
解答:$$a=\sqrt{14+\sqrt{21}} \Rightarrow \sqrt{14+\sqrt{16}}\lt a\lt \sqrt{14+\sqrt{25}} \Rightarrow 4\lt\sqrt{18} \lt a\lt \sqrt{19}\lt 5 \\ \Rightarrow 4\lt a\lt 5,故選\bbox[red, 2pt]{(B)}$$
解答:$$\cases{\lim_{x\to 1}{f(x)\over x-1}=-3\\ \lim_{x\to 2}{f(x)\over x-2}=5 } \Rightarrow \cases{f(x)=(x-1)g(x) 且g(1)=-3\\ f(x)=(x-2)h(x)且h(2)=5} \\ \Rightarrow f(x)=(x-1)(x-2)(ax+b) \Rightarrow \cases{-(a+b)=-3\\ 2a+b=5} \Rightarrow \cases{a=2\\b=1} \\ \Rightarrow f(x)=(x-1)(x-2)(2x+b) \Rightarrow f(0)=2b=2,故選\bbox[red, 2pt]{(A)}$$
解答:$$\cases{(\log 3)x+ \log y=\log 2\\ (\log 9)x+3\log y=\log 16} \Rightarrow \cases{\log (3^x\cdot y)=\log 2\\ \log (9^x\cdot y^3) =\log 16} \Rightarrow \cases{y3^x=2 \Rightarrow y=2/3^x\\ y^33^{2x}=16} \\ \Rightarrow ({2\over 3^x})^3 \cdot 3^{2x} ={8\over 3^x}=16 \Rightarrow 3^x={1\over 2} \Rightarrow y=2/3^x=4 \Rightarrow 3^a+b={1\over 2}+4={9\over 2},故選\bbox[red, 2pt]{(C)}$$
解答:$$f(x)=x^{10}+2x+1 \Rightarrow f'(x)=10x^9+2 \Rightarrow f'(-1)=-8 \\ \Rightarrow \lim_{h\to 0}{f(2h-1)-f(-1)\over h} = \lim_{h\to 0}{(f(2h-1)-f(-1))'\over (h)'} = \lim_{h\to 0}{2f'(2h-1) \over 1} = 2f'(-1)= -16\\,故選\bbox[red, 2pt]{(A)}$$
解答:$$f(x)=(x+1)p(x)-1= (x-2)q(x)+5=(x^2-x-2)r(x)+ax+b \\\quad =(x-2)(x+1)r(x)+ax+b \Rightarrow \cases{f(-1)=-1=-a+b\\ f(2)=5=2a+b} \Rightarrow \cases{a=2\\ b=1} \\ \Rightarrow 餘式為2x+1,故選\bbox[red, 2pt]{(B)}$$
解答:$$\cos 60^\circ ={\vec a\cdot \vec b\over |\vec a||\vec b|} \Rightarrow \vec a\cdot \vec b={1\over 2} \cdot 1\cdot 3={3\over 2} \\ \Rightarrow (2\vec a-\vec b)\cdot (2\vec a-\vec b) =4|\vec a|^2-4\vec a\cdot \vec b+|\vec b|^2 = 4-6+9=7 \Rightarrow |2\vec a-\vec b|=\sqrt 7,故選\bbox[red, 2pt]{(D)}$$
解答:$$\cases{\log_{(5-x) } (-x^2+10x-5)\\ \log_{(5-x)}(2x+10)} \Rightarrow \cases{5-x\gt 0\\ -x^2+10x-5\gt 0\\ 2x+10\gt 0} \Rightarrow \cases{5\gt x\\ 5-2\sqrt 5 \lt x\lt 5+2\sqrt 5 \\ x\gt -5} \\\Rightarrow 5-2\sqrt 5\lt x\lt 5 \cdots(1);\; 又\cases{5-x\gt 1 \Rightarrow -x^2+10x-5 \lt 2x+10 \Rightarrow x\lt 3\cdots(2)\\ 5-x\lt 1 \Rightarrow -x^2+10x-5 \gt 2x+10 \Rightarrow 4\lt x\lt 5 \cdots(3)} \\ \Rightarrow \cases{ (1)\cap (2) \Rightarrow 5-2\sqrt 5\lt x\lt 3\\ (1)\cap (3) \Rightarrow 4\lt x\lt 5 },故選\bbox[red, 2pt]{(D)}$$
解答:$$\begin{vmatrix} -1& 2& -1\\ 1& 1& 2\\ 0 & 1& 3\end{vmatrix} =-3-1+0-0-6+2=-8,故選\bbox[red, 2pt]{(B)}$$
解答:$$\cases{A(1,-1,1) \\B(-3,2,1) \\C(5,-4,3)} \Rightarrow \cases{\vec u= \overrightarrow{AB}=(-4,3,0) \\ \vec v= \overrightarrow{AC} =(4,-3,2)} \Rightarrow \vec n=\vec u\times \vec v=(6,8,0) \\ \Rightarrow S_{\triangle ABC} ={1\over 2}\Vert \vec n\Vert ={1\over 2} \sqrt{6^2+8^2} =5,故選\bbox[red, 2pt]{(C)}$$
解答:$$\#(A\cup B\cup C)= \#(A)+ \#(B)+ \#(C)- \#(A\cap B)-\#(B\cap C)- \#(C\cap A)+ \#(A\cap B\cap C) \\ =28+29+25-10-11-12+3=52,故選\bbox[red, 2pt]{(B)}$$
解答:$$z+z^{-1}= -\sqrt 3 \Rightarrow z^2+\sqrt 3z+1=0 \Rightarrow z=-{\sqrt 3\over 2}+{1\over 2}i =e^{5\pi i/6} \\ \Rightarrow z^{10} +z^{-10} =e^{50\pi i/6}+ e^{-50\pi /6} = 2\cos {50\over 6}\pi =2\cos {\pi\over 3} =1,故選\bbox[red, 2pt]{(A)}$$
解答:$$\lim_{x\to \infty} {x-\sin x\over x} =\lim_{x\to \infty} \left(1-{\sin x\over x}\right) = 1-0=1,故選\bbox[red, 2pt]{(A)}$$
解答:$$\int_0^3 x[x]\,dx = \int_0^1 0\,dx +\int_1^2 x \,dx +\int_2^3 2x\,dx = 0+{3\over 2}+4={11\over 2},故選\bbox[red, 2pt]{(D)}$$
解答:$$x^3+y^3-9xy=0 \Rightarrow 3x^2+3y^2y'-9y-9xy'=0 \Rightarrow y'={9y-3x^2\over 3y^2-9x} \\ \Rightarrow y'(2,4)={36-12\over 48-18} ={24\over 30}={4\over 5},故選\bbox[red, 2pt]{(D)}$$
解答:$$A為5\times 3 \Rightarrow A^T=3\times 5 \Rightarrow B為5\times n,又C為7\times 4 \Rightarrow n=7 \Rightarrow B為5\times 7,故選\bbox[red, 2pt]{(A)}$$
解答:$$\cases{\tan \alpha +\tan \beta=-{b\over a} \\ \tan \alpha \tan \beta= {c\over a}} \Rightarrow \tan(\alpha+\beta) ={\tan \alpha+ \tan \beta\over 1-\tan \alpha \tan \beta} ={-b/a\over 1- c/a} =-{b\over a-c }\\ \Rightarrow \cot(\alpha+\beta) ={c-a\over b},故選\bbox[red, 2pt]{(D)}$$
解答:$$\left(x+{1\over x} \right)^2 =x^2+{1\over x^2}+2 \Rightarrow 2\left(x^2+{1\over x^2} \right)-9\left(x+{1\over x} \right) +14 =2\left(x+{1\over x} \right)^2-9\left(x+{1\over x} \right) +10 \\=\left( 2\left(x+{1\over x} \right)-5\right) \left( \left(x+{1\over x} \right)-2\right)=0 \Rightarrow\cases{x+{1\over x}={5\over 2} \\x+{1\over x}=2} \Rightarrow \cases{2x^2-5x+2=0\\ x^2-2x+1=0} \\ \Rightarrow \cases{(2x-1)(x-2)=0\\ (x-1)^2=0} \Rightarrow x={1\over 2},1,2,故選\bbox[red, 2pt]{(C)}$$
解答:$$\lim_{x\to 0} {1-\cos x\over x^2} =\lim_{x\to 0} {(1-\cos x)'\over (x^2)'} = \lim_{x\to 0} { \sin x\over 2x} = \lim_{x\to 0} { (\sin x)'\over (2x)'} = \lim_{x\to 0} { \cos x\over 2} ={1\over 2},故選\bbox[red, 2pt]{(B)}$$
解答:$$4x^3-24x^2+23x+18=0 \Rightarrow \cases{三根之和=6\\ 三根之積=-9/2},故選\bbox[red, 2pt]{(B)}$$
解答:$$f(x)=(x+2)(x+5)^2 \Rightarrow f'(x)=(x+5)^2+2(x+2)(x+5) =(x+5)(3x+ 9) \\ \Rightarrow f''(x)=3x+9+3x+15 =6x+24\\ f''(x)=0 \Rightarrow x=-4 \Rightarrow 反曲點(-4,f(-4)) =(-4,-2),故選\bbox[red, 2pt]{(C)}$$











































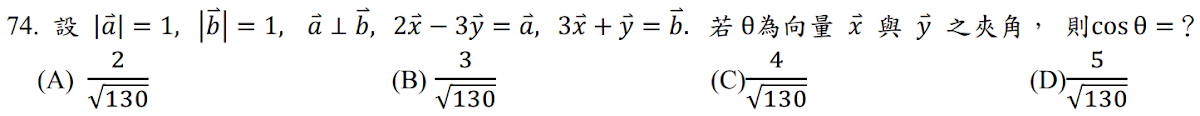


























沒有留言:
張貼留言