教育部113年自學進修專科學校學力鑑定考試試題本
專業科目(一): 微積分
解答:$$f(x)=x^4-4x^3 \Rightarrow f'(x)=4x^3-12x^2=4x^2(x-3)\ge 0 \Rightarrow x\ge 3,故選\bbox[red, 2pt]{(D)}$$解答:$$f(x,kx)= {x\cdot kx\over x^2+k^2x^2}={k\over k^2+1} \Rightarrow \lim_{x\to 0} f(x,kx)={k\over k^2+1} \ne 0 (若k\ne 0)\\ \Rightarrow f(x,y)在原點極限不存在\Rightarrow f(x)原點不可微分,故選\bbox[red, 2pt]{(D)}$$
解答:$$f(x,y)= x^4+xy^2-3y^3 \Rightarrow f_y(x,y)=2xy-9y^2 \Rightarrow f_y(2,1) =4-9=-5,故選\bbox[red, 2pt]{(B)}$$
解答:$$\int y^2 \pi\,dx = \int_0^1 x\pi\,dx ={1\over 2}\pi,故選\bbox[red, 2pt]{(B)}$$
解答:$$\lim_{x\to \infty} {\sin e^{-x}\over e^{-x}} =\lim_{x\to \infty} {(\sin e^{-x})'\over (e^{-x})'} =\lim_{x\to \infty} {-e^{-x}\cos e^{-x}\over -e^{-x}} =\lim_{x\to \infty} \cos e^{-x} = \cos 0=1,故選\bbox[red, 2pt]{(B)}$$
解答:$$(A)\times: 對t\gt 0而言,P(t)並非皆遞增\\ (B)\times:對t\gt 0而言,P(t)並非皆凹向下\\ (C)\times: P(t_1)為凹向下,因此P''(t_1)\lt 0\\ (D)\bigcirc: P(t_2)為凹向上,因此P''(t_2)\gt 0\\,故選\bbox[red, 2pt]{(D)}$$
解答:$$\lim_{x\to 1^+}\left({1\over \ln x}-{1\over x-1} \right) =\lim_{x\to 1^+} {x-1-\ln x\over (x-1)\ln x} =\lim_{x\to 1^+} {(x-1-\ln x)'\over ((x-1)\ln x)'} =\lim_{x\to 1^+} { 1-1/ x\over \ln x+(x-1)/x} \\ =\lim_{x\to 1^+} {x-1 \over x\ln x+x-1} =\lim_{x\to 1^+} {(x-1)' \over (x\ln x+x-1)'} =\lim_{x\to 1^+} {1 \over \ln x+1+1} ={1\over 2},故選\bbox[red, 2pt]{(C)}$$
解答:$$\lim_{n\to \infty} \left({1\over 2+{1\over n}} +{1\over 2+{2\over n}} + \cdots +{1\over 2+{n\over n}} \right){1\over n} =\lim_{n\to \infty} \sum_{k=1}^n {1\over 2+{k\over n}} \cdot {1\over n} =\int_0^1 {1\over 2+x}\,dx \\= \ln 3-\ln 2 =\ln{3\over 2},故選\bbox[red, 2pt]{(B)}$$
解答:$$\int_1^2 (4-z^2)\pi\,dz= \pi\left. \left[ 4z-{1\over 3}z^3 \right] \right|_1^2 =\left( 8-{8\over 3}\right)\pi-\left(4-{1\over 3} \right)\pi={5\over 3}\pi,故選\bbox[red, 2pt]{(B)}$$
解答:$$\cases{x=s^2t\\ y=st^2} \Rightarrow \displaystyle \cases{\displaystyle \frac{\partial x}{\partial t} =s^2\\ \displaystyle \frac{\partial y}{\partial t} =2st} \Rightarrow \frac{\partial z}{\partial t} =\frac{\partial z}{\partial x}\frac{\partial x}{\partial t} + \frac{\partial z}{\partial y} \frac{\partial y}{\partial t} = y^2\cdot s^2+2xy\cdot 2st =s^4t+4s^4t^4 \\ \Rightarrow \Rightarrow \frac{\partial z}{\partial t} (2,1) =16+64=80,故選\bbox[red, 2pt]{(C)}$$
解答:
$$積分區域為一三角形,如上圖。因此\int_0^1 \int_0^{2y} f(x,y)\,dxdy = \int_0^2 \int_{x/2}^1 f(x,y)\,dydx,故選\bbox[red, 2pt]{(A)}$$
解答:$$e^y+\sin(x)=1 \Rightarrow \cases{y'e^y+ \cos (x)=0 \\ y= \ln(1-\sin (x))} \Rightarrow \cases{y'=-{\cos x\over e^y} \\ y(\pi) =\ln 1=0} \Rightarrow f'(\pi)=y'(\pi) =-{\cos \pi \over e^{y(\pi)}} \\=-{-1\over e^0} =1,故選\bbox[red, 2pt]{(A)}$$
解答:$$\lim_{x\to 1} {\sqrt x-1\over x^3-1} =\lim_{x\to 1} {(\sqrt x-1)' \over (x^3-1)'} =\lim_{x\to 1} {1/2\sqrt x\over 3x^2} =\lim_{x\to 1} { 1\over 6x^3 \sqrt x} = {1\over 6},故選\bbox[red, 2pt]{(A)}$$
解答:$$\int{1\over 1-x^2}\,dx =\int{1\over (1-x)(1+x)}\,dx ={1\over 2} \int \left( {1\over 1-x}+{1\over 1+x}\right) \,dx ={1\over 2}(-\ln(1-x)+ \ln(1+x)) +C\\={1\over 2 }\ln({1+x\over 1-x}) +C,故選\bbox[red, 2pt]{(D)}$$
解答:$${1\over 2}\int r^2\,d\theta= {1\over 2} \int_{-\pi/4}^{\pi/4} \cos^2(2\theta)\,d\theta = {1\over 4} \int_{-\pi/4}^{\pi/4} (\cos(4\theta)+1)\,d\theta = {1\over 4} \left. \left[ {1\over 4}\sin 4\theta+\theta \right] \right|_{-\pi/4}^{\pi/4} \\={1\over 4}\cdot {\pi\over 2} ={\pi \over 8},故選\bbox[red, 2pt]{(D)}$$
解答:$$\cases{x+2y+z=2\\ x=2y\\ x=0\\z=0} \Rightarrow 四面體頂點\cases{O(0,0,0)\\ A(0,1,0)\\ B(1,1/2,0)\\C(0,0,2)} \Rightarrow \cases{\triangle OAB面積={1\over 2} \\ \overline{OC}=2} \\ \Rightarrow 四面體體積={1\over 3}\cdot {1\over 2}\cdot 2={1\over 3},故選\bbox[red, 2pt]{(A)}$$
解答:$$g(x)=x^2 \Rightarrow g'(x)=2x \Rightarrow g''(x)=2\\ f(x)=e^{g(x)} \Rightarrow f'(x)=g'(x)e^{g(x)} \Rightarrow f''(x)=g''(x)e^{g(x)}+ (g'(x))^2 e^{g(x)} \\ \Rightarrow f''(0) =g''(0)f(0)+(g'(0))^2f(0) =2\cdot 1+0=2,故選\bbox[red, 2pt]{(B)}$$
解答:$$u=3x^2+1 \Rightarrow du=6x\,dx \Rightarrow \int_0^1 {2x\over 3x^2+1}\,dx = \int_{1}^{49} {1/3\over u}du ={1\over 3}(\ln 49-\ln 1) ={2\over 3}\ln 7,故選\bbox[red, 2pt]{(A)}$$
解答:$$f(t)=\int_1^{t^2} {\cos (x+1)\over x}\,dx \Rightarrow f'(t) ={\cos(t^2+1) \over t^2} \cdot (t^2)'={2\cos(t^2+1)\over t},故選\bbox[red, 2pt]{(B)}$$
解答:
解答:$$e^y+\sin(x)=1 \Rightarrow \cases{y'e^y+ \cos (x)=0 \\ y= \ln(1-\sin (x))} \Rightarrow \cases{y'=-{\cos x\over e^y} \\ y(\pi) =\ln 1=0} \Rightarrow f'(\pi)=y'(\pi) =-{\cos \pi \over e^{y(\pi)}} \\=-{-1\over e^0} =1,故選\bbox[red, 2pt]{(A)}$$
解答:$$\lim_{x\to 1} {\sqrt x-1\over x^3-1} =\lim_{x\to 1} {(\sqrt x-1)' \over (x^3-1)'} =\lim_{x\to 1} {1/2\sqrt x\over 3x^2} =\lim_{x\to 1} { 1\over 6x^3 \sqrt x} = {1\over 6},故選\bbox[red, 2pt]{(A)}$$
解答:$$\int{1\over 1-x^2}\,dx =\int{1\over (1-x)(1+x)}\,dx ={1\over 2} \int \left( {1\over 1-x}+{1\over 1+x}\right) \,dx ={1\over 2}(-\ln(1-x)+ \ln(1+x)) +C\\={1\over 2 }\ln({1+x\over 1-x}) +C,故選\bbox[red, 2pt]{(D)}$$
解答:$${1\over 2}\int r^2\,d\theta= {1\over 2} \int_{-\pi/4}^{\pi/4} \cos^2(2\theta)\,d\theta = {1\over 4} \int_{-\pi/4}^{\pi/4} (\cos(4\theta)+1)\,d\theta = {1\over 4} \left. \left[ {1\over 4}\sin 4\theta+\theta \right] \right|_{-\pi/4}^{\pi/4} \\={1\over 4}\cdot {\pi\over 2} ={\pi \over 8},故選\bbox[red, 2pt]{(D)}$$
解答:$$\cases{x+2y+z=2\\ x=2y\\ x=0\\z=0} \Rightarrow 四面體頂點\cases{O(0,0,0)\\ A(0,1,0)\\ B(1,1/2,0)\\C(0,0,2)} \Rightarrow \cases{\triangle OAB面積={1\over 2} \\ \overline{OC}=2} \\ \Rightarrow 四面體體積={1\over 3}\cdot {1\over 2}\cdot 2={1\over 3},故選\bbox[red, 2pt]{(A)}$$
解答:$$g(x)=x^2 \Rightarrow g'(x)=2x \Rightarrow g''(x)=2\\ f(x)=e^{g(x)} \Rightarrow f'(x)=g'(x)e^{g(x)} \Rightarrow f''(x)=g''(x)e^{g(x)}+ (g'(x))^2 e^{g(x)} \\ \Rightarrow f''(0) =g''(0)f(0)+(g'(0))^2f(0) =2\cdot 1+0=2,故選\bbox[red, 2pt]{(B)}$$
解答:$$u=3x^2+1 \Rightarrow du=6x\,dx \Rightarrow \int_0^1 {2x\over 3x^2+1}\,dx = \int_{1}^{49} {1/3\over u}du ={1\over 3}(\ln 49-\ln 1) ={2\over 3}\ln 7,故選\bbox[red, 2pt]{(A)}$$
解答:$$f(t)=\int_1^{t^2} {\cos (x+1)\over x}\,dx \Rightarrow f'(t) ={\cos(t^2+1) \over t^2} \cdot (t^2)'={2\cos(t^2+1)\over t},故選\bbox[red, 2pt]{(B)}$$
解答:

$$(A)\times: f(1)=0為絕對最小值\\ (B)\times: f(2)=\ln 2為相對最大值\\ (C)\bigcirc:f'(x)=\cases{{1\over x},x\ge 1\\ -{1\over x}, x\le 1} \Rightarrow f''(x)=\cases{-{1\over x^2},x\ge 1\\ {1\over x^2}, x\le 1} \Rightarrow \cases{f''(1^+)\lt 0\\ f''(1^-)\gt 0} \Rightarrow (1,f(1))是反曲點 \\(D)\times: \cases{f(x)為遞減, 0\lt x\le 1\\ f(x)為遞增,1\le x\le 2}\\,故選\bbox[red, 2pt]{(C)}$$
======================= END ======================
解題僅供參考,學力鑑定歷年試題及詳解



















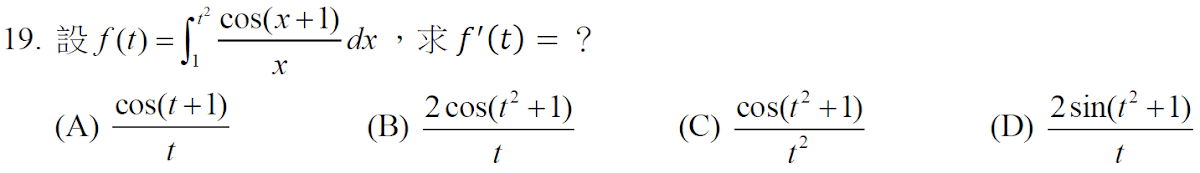


沒有留言:
張貼留言