114年台科機械碩士班丙組-工程數學詳解

國立臺灣科技大學114學年度碩士班招生試題

系所組別:機械工程系碩士班丙組
科目:工程數學

解答: $${dy\over dx}=-4x^2y \Rightarrow {1\over y}dy =-4x^2\,dx \Rightarrow \int {1\over y}dy = \int-4x^2\,dx \Rightarrow \ln y=-{4\over 3}x^3+c_1 \\ \Rightarrow y=e^{-4x^3/3+c_1} =c_2e^{-4x^3/3} \Rightarrow y(0)=c_2=2 \Rightarrow \bbox[red, 2pt]{y=2e^{-4x^3/3}}$$

解答: $$\textbf{(a) }{d^3y\over dx^3}+3{d^2y\over dx^2}+3{dy\over dx}+y=0 \Rightarrow \lambda^3+3\lambda^2+ 3\lambda+1=0 \Rightarrow (\lambda+1)^3=0 \Rightarrow \lambda=-1\\ \qquad \Rightarrow \bbox[red, 2pt]{y_h= c_1e^{-x}+ c_2xe^{-x}+c_3x^2 e^{-x}} \\ \textbf{(b) }y_p=Ax^3e^{-x} \Rightarrow y_p'=3Ax^2e^{-x} -Ax^3e^{-x} \Rightarrow y_p''=6Axe^{-x}-6Ax^2e^{-x}+Ax^3e^{-x} \\ \qquad \Rightarrow y_p'''= 6Ae^{-x}-18Axe^{-x} +9Ax^2e^{-x}  -Ax^3e^{-x} \\\qquad \Rightarrow y_p'''+3y_p''+ 3y_p'+y_p=6Ae^{-x} =30e^{-x} \Rightarrow A=5 \Rightarrow \bbox[red, 2pt]{y_p=5x^3e^{-x}}$$

解答: $$\textbf{(a) }\cases{u=e^{-st} \\dv=f'(t)\,dt} \Rightarrow \cases{du= -se^{-st}\,dt\\ v=f(t)} \\\quad \Rightarrow L\{f'(t)\} =\int_0^\infty f'(t)e^{-st}\,dt = \left. \left[f(t)e^{-st} \right] \right|_0^\infty+s \int_0^\infty f(t)e^{-st}\,dt =0-f(0)+sL\{f(t)\} \\ \quad \Rightarrow L(f')=sL(f)-f(0)\qquad \bbox[red, 2pt]{QED}\\ \textbf{(b) } \text{ By (a), we have }L(f'')=sL(f')-f'(0) =s(sL(f)-f(0))-f'(0)\\\quad \Rightarrow L(f'')=s^2L(f)-sf(0)-f'(0) \quad \bbox[red, 2pt]{QED}\\ \textbf{(c) } f=\cos at \Rightarrow f'=-a\sin at \Rightarrow L(f')=sL(f)-f(0) \\ \quad \Rightarrow L(-a\sin at)= sL(\cos at)-\cos (0) \Rightarrow -aL(\sin at)={s^2\over s^2+a^2}-1={-a^2\over s^2+a^2} \\ \Rightarrow L(\sin at)={a\over s^2+a^2} \Rightarrow L(t \sin at) =-{d\over ds}\left(a\over s^2+a^2 \right) =\bbox[red, 2pt]{2as \over (s^2+a^2)^2}$$


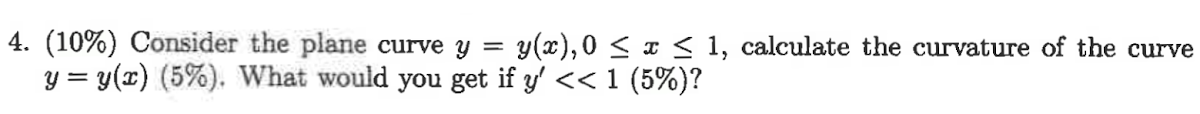
解答: $$\text{curvature }K(x)={|y''(x)|\over (1+(y'(x))^2)^{3/2})}\\ y'<<1 \Rightarrow K(x) \sim|y''|$$

解答: $$\textbf{(a) }F(\omega) =\int_{-\infty}^\infty f(t)e^{-j\omega t}\,dt\\\textbf{(b)}  f(t)={1\over 2\pi} \int_{-\infty}^\infty F(\omega )e^{j\omega t} \,d\omega \\\textbf{(c) } F(\omega) =\int_{-\infty}^\infty f(t)e^{-j\omega t}\,dt =\int_{-T}^T e^{-j\omega t}\,dt = \left. \left[ -{1\over j\omega} e^{-j\omega t}\right] \right|_{-T}^T =-{1\over j\omega }\left( e^{-j\omega T} -e^{j\omega T}\right) \\\qquad =-{1\over j\omega}(\cos(\omega T)- j\sin(-\omega T) -\cos(\omega T)-j\sin(\omega T)) =-{1\over j\omega} \cdot (-2j\sin(\omega T)) =\bbox[red, 2pt]{2\sin(\omega T) \over \omega} \\\textbf{(d) } \int_{-\infty}^\infty {\cos (2\omega) \sin (3\omega)\over \omega} \,d\omega = \int_{-\infty}^\infty {1\over 2\omega}(\sin(5\omega)+ \sin(\omega)) \,d\omega \\ = {1\over 2}\int_{-\infty}^\infty \left({ \sin (5\omega)  \over \omega} +{ \sin \omega \over \omega} \right)\,d\omega ={1\over 2}(\pi +\pi) =\bbox[red, 2pt] \pi\\ \bbox[cyan, 2pt]{註}:f(t)= \int_{-\infty}^\infty {\sin (tx)\over x}\,dx \Rightarrow L\{f(t)\} = \int_0^\infty\int_{-\infty}^\infty {\sin (tx)\over x}\,dx e^{-st}\,dt =\int_{-\infty}^\infty {1\over x}\int_0^\infty \sin(tx)e^{-st}\,dt dx \\=\int_{-\infty}^\infty {1\over x}L\{ \sin(tx)\} \,dx =\int_{-\infty}^\infty {1\over x}{x\over s^2+x^2} \,dx =\int_{-\infty}^\infty {1\over s^2+x^2}\,dx =\oint {1\over s^2+z^2}\,dz \\ =\oint {1\over (z+is)(z-is)}\,dz =2\pi i \cdot {1\over 2is} ={\pi\over s} \Rightarrow f(t)=L^{-1}\{{\pi\over s}\} = \bbox[cyan,2pt]{\pi}$$

解答: $$\text{Let }u(r,\theta)= R(r)\Theta(\theta) \Rightarrow R''\Theta+ {1\over r}R'\Theta+{1\over r^2}R\Theta''=0 \Rightarrow {r^2R''+rR'\over R} =-{\Theta''\over \Theta} =k^2 \ge 0 \\ \Rightarrow \cases{\Theta''+k^2 \Theta=0 \cdots(1) \\r^2R''+ rR'-k^2R=0 \cdots(2) } \\(1)\Theta''+k^2\Theta=0 \Rightarrow \Theta =c_1 \cos (k\theta)+ c_2 \sin(k\theta) \Rightarrow \Theta'= -c_1k\sin(k\theta) +c_2k \cos(k\theta) \\ \quad \cases{u_\theta(r,0)= R(r)\Theta'(0) =0\\ u_\theta(r, \pi/2) = R(r)\Theta'(\pi/2) =0}  \Rightarrow \cases{\Theta'(0)=0\\ \Theta'( \pi/2)=0} \Rightarrow \cases{c_2k=0\\ -c_1k\sin(k\pi/2)+ c_2k \cos(k\pi/2) =0} \\\quad \Rightarrow c_2=0 \Rightarrow \sin(k\pi/2)=0  \Rightarrow k=2n \Rightarrow \Theta_n(\theta)= \cos(2n\theta),n=0,1,2,\dots\\ (2) r^2R''+rR'-k^2R=0 \Rightarrow r^2R''+rR'-4n^2R=0 \Rightarrow R=c_1r^{2n}+c_2 r^{-2n} \\\quad \Rightarrow R_n(r)=r^{2n} \quad (\because |u(0,\theta)|\lt \infty \Rightarrow |R(0)|\lt \infty)\\ u_n(r,\theta)= A_n \cos(2n\theta) B_n r^{2n} \Rightarrow \bbox[red, 2pt]{u(r,\theta)= \sum_{n=0}^\infty C_n r^{2n} \cos(2n\theta)} \\ \Rightarrow u_r(r, \theta)= \sum_{n=1}^\infty 2nC_n r^{2n-1} \cos(2n\theta) \Rightarrow u_r(1,\theta)= f(\theta) =\sum_{n=1}^\infty 2nC_n  \cos(2n\theta) \\ \Rightarrow 2nC_n={2\over \pi/2} \int_0^{\pi/2} f(\theta)\cos(2n\theta)\,d\theta \Rightarrow \bbox[red, 2pt]{C_n={2\over n\pi} \int_0^{\pi/2} f(\theta) \cos(2n\theta)\,d\theta, n=1,2,\dots}\\ \bbox[red, 2pt]{C_0={2\over \pi} \int_0^{\pi/2} f(\theta)\,d\theta}\\ f(\theta) = \sin(2\theta) \Rightarrow C_0 ={2\over \pi} \int_0^{\pi/2} \sin(2\theta)\,d\theta ={2\over \pi} \left. \left[ -{1\over 2}\cos 2\theta \right] \right|_0^{\pi/2} \Rightarrow \bbox[red, 2pt]{C_0={1\over 2}} \\ \Rightarrow C_n={2\over n\pi} \int_0^{\pi/2} \sin(2\theta) \cos(2n\theta)\,d\theta ={2\over n\pi} \cdot {1+(-1)^n\over 2-2n^2} \Rightarrow \bbox[red, 2pt]{C_n={1+(-1)^n \over n(1-n^2)\pi}}$$

========================== END =========================

解題僅供參考，碩士班歷年試題及詳解