107年桃連區內壢高中特招數學詳解

解：

$|A|=|B|且|A-B|=6\Rightarrow A=3,B=-3$，故選$\bbox[red,2pt]{(B)}$。

---

解：

灰色區域左上角日期為a，則右邊為a+1、下方為a+7及右下角為a+8，日期和為$4a+16=80  \Rightarrow   a=16$，也就是4月16日星期三$\Rightarrow$4月23日星期三$\Rightarrow$4月30日星期三，因此五月一日星期四，故選$\bbox[red,2pt]{(C)}$。

---

解：

上圖為一個邊長8+4=12的大正方形，面積為$12\times  12=144$；大正方形有四塊小長方形所圍住，四個小長方形的面積為$8\times  4\times   4=128$。因此灰色小正方形面積為144-128=16，故選$\bbox[red,2pt]{(B)}$。

---

解：
$$\begin{cases} a=\frac { 6\times { 10 }^{ 2017 } }{ 2.4\times { 10 }^{ 2018 } } =\frac { 1 }{ 0.4\times { 10 } } =0.25 \\ b=\frac { 1.2\times { 10 }^{ -2017 } }{ 3\times { 10 }^{ -2018 } } =\frac { 0.4\times { 10 } }{ 1 } =4 \end{cases}\Rightarrow b>1>a>0$$ 故選$\bbox[red,2pt]{(A)}$。

---

解：
假設大圓半徑$b$，小圓半徑$a$，則$\triangle AOB=\frac{b^2}{2}$，$\triangle   COD=\frac{a^2}{2}$，灰色面積=$\frac{b^2}{2}-\frac{a^2}{2}=25\Rightarrow   b^2-a^2=50$。
大小兩圓面積差為$b^2\pi-a^2\pi=(b^2-a^2)\times\pi=50\times\pi=157$，故選$\bbox[red,2pt]{(B)}$。

---

解：
由題意知$(a-1)^2<520<a^2$；又$23^2=529,22^2=484$，因此$a=23$，故選$\bbox[red,2pt]{(C)}$。

---

解： $$\begin{cases} y=x+k \\ y=kx-2 \end{cases}\Rightarrow x+k=kx-2\Rightarrow (k-1)x=k+2\Rightarrow x=\frac { k+2 }{ k-1 }$$

只有$k=4\Rightarrow x=2$為整數，其它均為分數，故選$\bbox[red,2pt]{(D)}$。

---

解：
(A)$21\to   奇數\to   21\times   4=84\to   84+23=107\ngtr   107$
(B)$22\to   偶數\to   22\times   5=110>107$
(C)與(D)皆輸出大於107的正整數

因此最小值為22，故選$\bbox[red,2pt]{(B)}$。

---

解：

由上圖可知B=(b,-a)，故選$\bbox[red,2pt]{(C)}$。

---

解：
$y=ax$通過(1,2)，可得$a=2$；$y=\frac{1}{2}x+b$通過(1,2)，可得$2=\frac{1}{2}+b\Rightarrow b=\frac{3}{2}$。因此聯立方程式 $$\begin{cases} x-2y+2b=0 \\ ax-y=0 \end{cases}\Rightarrow \begin{cases} x-2y+3=0 \\ 2x-y=0 \end{cases}\Rightarrow x-4x+3=0\Rightarrow x=1\Rightarrow y=2$$ ，故選$\bbox[red,2pt]{(D)}$。

---

解：

原函式圖形如上圖左，向下移動3單位後如上圖右。注意P點位置，原P點y坐標介於1與3之間，往下移動3單位後，P點的y坐標為負值。因此移動後的函式有兩相異正根，故選$\bbox[red,2pt]{(B)}$。

---

解：

邊長為8公分的正方體體積為$8^3=512$立方公分；一個直角柱的體積為$1^3\div 2=\frac{1}{2}$；因此需要$512\div (1/2) =1024$個直角柱，故選$\bbox[red,2pt]{(B)}$。

---

解：
$y=x^2-2x-1=(x-1)^2-2\Rightarrow$對稱軸為x=1；
$y=ax^2+bx=x(ax+b)\Rightarrow$與x軸交於(0,0)、$A=(-\frac{b}{a},0)$且頂點的x坐標$-\frac{b}{2a}=1\Rightarrow   2a=-b\Rightarrow A=(2,0)$，故選$\bbox[red,2pt]{(A)}$。

---

解：

甲班平均時數: $(3.8\times 32+3.3\times 8)\div 40=148\div 40=3.7$
乙班平均時數: $(4\times 27+3\times 18)\div 45=162\div 45=3.6$
丙班平均時數: $(3.4\times 28+4.4\times 12)\div 40=148\div 40=3.7$
丁班平均時數: $(3.6\times 15+3.9\times 30)\div 45=171\div 45=3.8$
故選$\bbox[red,2pt]{(D)}$。

---

解：

假設正三角形的邊長為$a$且$\overline{AM}=b$，如上圖。
AMN與BCNM周長相等，即$2b+\overline{MN}=\overline{MN}+3a-2b\Rightarrow    b=\frac{3a}{4}$
因此$\frac{\overline{MN}}{\overline{BC}}=\frac{\overline{AM}}{\overline{AB}}=\frac{b}{a}=\frac{3}{4}\Rightarrow  \overline{BC}:\overline{MN}=4:3$，故選$\bbox[red,2pt]{(A)}$。

---

解：

若$\overline{OP}\bot\overline{AB}$，則$\overline{AB}$為最短的弦。
由直角$\triangle   AOP\Rightarrow   \overline{AP}=6\Rightarrow   \overline{AB}=6\times   2=12$
過P點之弦長至少為12，因此不可能為11，故選$\bbox[red,2pt]{(A)}$。

---

解： $$\begin{cases} x=10 \\ x=7 \\ x=5 \end{cases}\Rightarrow \begin{cases} -180b=720 \\ -30c=210 \\ 20a=60 \end{cases}\Rightarrow \begin{cases} b=-4 \\ c=-7 \\ a=3 \end{cases}\Rightarrow ab+c=3\times (-4)-7=-19$$ ，故選$\bbox[red,2pt]{(A)}$。

---

解：

$\triangle ABC$為直角三角形，所以外接圓圓心為O，如上圖。
令$\overline{AD}=a$，則圓半徑為$a+7$。
$${\overline{DC}}^2={\overline{AC}}^2-{\overline{DA}}^2={\overline{OC}}^2-{\overline{OD}}^2\Rightarrow 30^2-a^2=(a+7)^2-7^2\Rightarrow 2a^2+14a-900=0\\ \Rightarrow (a-18)(a+25)=0\Rightarrow a=18\Rightarrow \overline{OB}=a+7=18+7=25$$ 故選$\bbox[red,2pt]{(D)}$。

---

解：

令$R$至$\overline{MN}$的距離為$a$，即$\overline{WR}=a$，如上圖。 $$\overline { WR } =a\Rightarrow \overline { MN } =2a,\overline { NR } =\sqrt { 2 } a\Rightarrow \overline { SR } =2\sqrt { 2 } a\Rightarrow \overline { PR } =4a\\ \Rightarrow \triangle PMN=\overline { MN } \times \overline { PW } \div 2=2a\times (4a-a)\div 2=3a^{ 2 }=6\Rightarrow a=\sqrt { 2 } \\ \overline { PR } =4a=\overline { EH } \Rightarrow \overline { AD } =\frac { 8a }{ \sqrt { 2 }  } =\frac { 8\times \sqrt { 2 }  }{ \sqrt { 2 }  } =8=\overline { AB }$$ ，故選$\bbox[red,2pt]{(B)}$。

---

解：

甲方法: 每位學生被抽中的機率皆為1/4
乙方法: 愛班人數最多，所以愛班學生被抽中的機率高於其他班學生
，故選$\bbox[red,2pt]{(D)}$。

---

解： $${\left(n+\sqrt{n}\right)}^2\le 1600\Rightarrow n+\sqrt{n}\le 40\\n=34\Rightarrow n+\sqrt{n}=34+5.X=39.X\le 40\\n=35\Rightarrow n+\sqrt{n}=35+5.X=40.X>40\\n=39,40\Rightarrow n+\sqrt{n}>40$$

，故選$\bbox[red,2pt]{(A)}$。

---

解：
令長為$a$、寬為$b$，則 $$\begin{cases} a^{ 2 }+b^{ 2 }=\left( 2\sqrt { 5 }  \right) ^{ 2 }=20 \\ ab=6 \end{cases}\Rightarrow \begin{cases} \left( a+b \right) ^{ 2 }=a^{ 2 }+b^{ 2 }+2ab=20+12=32 \\ \left( a-b \right) ^{ 2 }=a^{ 2 }+b^{ 2 }-2ab=20-12=8 \end{cases}\\ \Rightarrow \begin{cases} a+b=4\sqrt { 2 }  \\ a-b=2\sqrt { 2 }  \end{cases}\Rightarrow a^{ 2 }-b^{ 2 }=\left( a+b \right) \left( a-b \right) =4\sqrt { 2 } \times 2\sqrt { 2 } =16$$ ，故選$\bbox[red,2pt]{(D)}$。

---

解：

${\overline{AB}}^2=0.5^2+3.5^2=\frac{25}{2}\Rightarrow \overline{AB}=\frac{5\sqrt{2}}{2}$，故選$\bbox[red,2pt]{(C)}$。

---

解：
21分鐘後，放進21/3=7球、拿出21/7=3球，箱子還有7-3=4球；
63分鐘後，箱子還有$4\times 3=12$球
66分→13球；69分→14球；70分鐘→13球；72分鐘→14球；75分鐘→15球；77分鐘→14球；
因此在下午1點14分(74分)時，箱子有14球，故選$\bbox[red,2pt]{(B)}$。

---

解：

令$\overline{AE}=\overline{EB}=a, \overline{DC}=b, \triangle AFD$面積=M, $\overline{AB}$與$\overline{DC}$的距離為h，如上圖。
$\triangle AEF\sim\triangle CDF(AAA)\Rightarrow \frac{\triangle AEF}{\triangle DCF}=\frac{{\overline{AE}}^2}{{\overline{DC}}^2}\Rightarrow \frac{64}{81}=\frac{a^2}{b^2}\Rightarrow a:b=8:9\Rightarrow a=8k,b=9k$ $$\begin{cases} \triangle ADC=bh\div 2=M+81 \\ \triangle AED=ah\div 2=M+64 \end{cases}\Rightarrow \frac { (b-a)h }{ 2 } =17\Rightarrow \frac { (9k-8k)h }{ 2 } =17\Rightarrow kh=34\\ \Rightarrow ABCD面積=\frac { (2a+b)h }{ 2 } =\frac { (16k+9k)h }{ 2 } =\frac { 25kh }{ 2 } =\frac { 25\times 34 }{ 2 } =425$$ ，故選$\bbox[red,2pt]{(C)}$。

---

解：

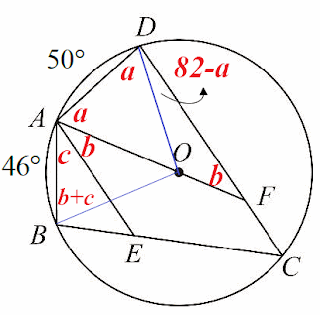
令$\angle DAO=a,\angle OAE=b,\angle EAB=c$，如上圖。

在等腰$\triangle OAD\Rightarrow 2a+\angle AOD=180\Rightarrow 2a+50=180\Rightarrow a=65^\circ$

$\triangle DAF\Rightarrow a+b+82=180\Rightarrow 65+b=98\Rightarrow b=33^\circ$

在等腰$\triangle OAB\Rightarrow 2(b+c)+\angle AOB=180\Rightarrow 2(33+c)+46=180 \Rightarrow c=34^\circ$

因此$\angle DAF-\angle BAE=a-c=65-34=31^\circ$，故選$\bbox[red,2pt]{(A)}$。

---

解：

假設$\angle   BAC=a,\angle  DAC=b,\angle   EAD=c$，見上圖。
$\triangle   ABD$與$\triangle   ACE$全等，因此$\angle   DAB=\angle   EAC\Rightarrow   a+b=b+c\Rightarrow    c=a$
 又$\angle   EAC=62^\circ\Rightarrow   b+c=62^\circ\Rightarrow   a+b=62^\circ\Rightarrow   \angle   DAB=62^\circ\Rightarrow  \angle  ADB=180-62-58=60^\circ$
在$\triangle  DAB$中，由於$\angle  ADB=60^\circ   >\angle   DBA=58^\circ\Rightarrow   \overline{AB}> \overline{AD}=\overline{AE}\Rightarrow   \overline{AB}>\overline{AE}$

在$\triangle  DAE$中，$\overline{AD}=\overline{AE}且\angle   EAD=a$；
在$\triangle  CAB$中，$\overline{AB}=\overline{AC}且\angle   CAB=a$；
由於$\overline{AB}>\overline{AE}\Rightarrow   \overline{BC}>\overline{DE}$

故選$\bbox[red,2pt]{(A)}$。

---

解：
每一個黑色五邊形的五個邊均與白色相鄰，但白色六邊形只有三個邊與黑色相鄰。
假設白色六邊形有$n$個，則$5\times   12=  n\times   3\Rightarrow   n=20$，故選$\bbox[red,2pt]{(C)}$。

---

解：

延長線段a與延長線e交於B、延長線段b與延長線d交於E，如上圖。
由於各內角均為120度，所以$\angle   DFE=\angle   FDE=\angle    CAB=\angle   BCA=60^\circ$，也就是說$\triangle   DEF$與$\triangle  ABC$均為正三角形，且$\overline{AB}//\overline{DE}$，因此$a+f=c+d$，故選$\bbox[red,2pt]{(C)}$。

---

解：

延長$\overline{AG}$交$\overline{BC}$於O，由於G是重心，所以O是$\overline{BC}$的中點，也就是圓心；延長$\overline{AG}$交$\overline{AC}$於H，由於G是重心，所以H是$\overline{AC}$的中點，見上圖。
假設$\overline{GC}=a$，在直角$\triangle BGC\Rightarrow   {\overline{BG}}^2=10^2-{\overline{GC}}^2=100-a^2$；
$\triangle  GBC=15=\overline{GC}\times\overline{BG}\div   2\Rightarrow a\times \sqrt{100-a^2}=30 \Rightarrow   (100-a^2)\times   a^2=900$
$\Rightarrow   (a^2-10)(a^2-90)=0\Rightarrow   a=\sqrt{10}\Rightarrow   \overline{GC}=\sqrt{10},\overline{BG}=3\sqrt{10}$
由於G是重心，所以$\overline{GH}=\overline{BG}\div   2=   \frac{3\sqrt{10}}{2}$
在直角$\triangle   GCH\Rightarrow   {\overline{HC}}^2={\overline{GC}}^2+{\overline{GH}}^2   =10+\frac{90}{4}  =\frac{130}{4}\Rightarrow   \overline{HC}=\frac{\sqrt{130}}{2}$
$\overline{AC}=2\overline{HC}=\sqrt{130}$，故選$\bbox[red,2pt]{(D)}$。

---

解：

$y=(x-1)(5-x)=-(x-3)^2+4\Rightarrow   A=(3,4)$，假設該水平線方程式為$y=a$，則$D=(3,a), B=(3-k,a),   C=(3+k,a)$，如上圖。
$\triangle ABC=\overline{BC}\times\overline{AD}\div   2=2k\times  (4-a)\div   2=(4-a)k=16k\Rightarrow   a=-12$
求水平線與二次函數的交點:   $(x-1)(5-x)=-12\Rightarrow   x^2-6x-7=0\Rightarrow   (x-7)(x+1)=0$
$\Rightarrow  x=7,-1\Rightarrow   2k=7-(-1)=8\Rightarrow   k=4$

答：k=$\bbox[red,2pt]{4}$

---

解：

延長$\overline{CD}$交$\overline{OB}$於E，作$\overline{DF}\bot\overline{OB}$，見上圖。
令$\overline{OC}=a\Rightarrow   \overline{CE}=a(\because   \angle   O=45^\circ)\Rightarrow   \overline{DE}=a-2$
$\overline{OE}=\sqrt{2}\times\overline{OC}=\sqrt{2}a\Rightarrow   \overline{FE}=\sqrt{2}a-a$
在直角$\triangle   DEF$中: $$\Rightarrow   {\overline{ED}}^2={\overline{DF}}^2+{\overline{EF}}^2   \Rightarrow   (a-2)^2=(\sqrt{2}a-a)^2+4   \Rightarrow   (2\sqrt{2}-2)a^2-4a=0 \\   \Rightarrow    a=\frac{4}{2\sqrt{2}-2}=\frac{4(2\sqrt{2}+2)}{4}=2\sqrt{2}+2$$

答：$\overline{OC}=\bbox[red,2pt]{2\sqrt{2}+2}$

---

- END -