高雄區公立高中 110 學年度聯合招考轉學生高二升高三
一、 單選題:（ 60 分）
解答：$$\sin 160^\circ\cos(-25^\circ)+ \cos(-20^\circ)\sin 25^\circ= \sin 20^\circ\cos(25^\circ)+ \cos(20^\circ)\sin 25^\circ \\= \sin(20^\circ+25^\circ) =\sin 45^\circ ={1\over \sqrt 2}，故選\bbox[red,2pt]{(A)}$$解答：$$1536\times({1\over 2})^n=3 \Rightarrow {1\over 2^n}={3\over 1536} ={1\over 512} ={1\over 2^9} \Rightarrow n=9，即需要9次的半衰期\\，也就9\times 8=72天，故選\bbox[red,2pt]{(D)}$$解答：$$\cases{2\vec u-\vec v=(1,-5)\\ 3\vec u+2\vec v=(19,-4)} \Rightarrow \cases{\vec u=(3,-2)\\ \vec v=(5,1)} \Rightarrow \vec u\cdot \vec v=15-2=13，故選\bbox[red,2pt]{(B)}$$解答：$$相當於圓心(-1,3)至L距離={-4+9+10\over \sqrt{4^2+3^2}} ={15\over 5}=3，再平方，即3^2=9，故選\bbox[red,2pt]{(C)}$$解答：$$假設邊長為1 \Rightarrow \overline{HB}=\sqrt 3 \Rightarrow \overline{OB}= \overline{OA}=\overline{HB}\div 2=\sqrt 3/2 \\\Rightarrow \cos \angle AOB = {\overline{OA}^2 +\overline{OB}^2-\overline{AB}^2 \over 2\times \overline{OA}\times \overline{OB}} ={3/4+3/4-1\over 3/2} ={1\over 3}，故選\bbox[red,2pt]{(A)}$$解答：$$\cases{x-y平面:z=0 \Rightarrow 法向量\vec u=(0,0,1) \\點(0,4,4)至點(3,8,t)向量\vec v=(3,4,t-4)}，\vec u與\vec v夾角45^\circ \Rightarrow \cos 45^\circ ={\vec u\cdot \vec v\over |\vec u||\vec v|} \\ \Rightarrow {1\over \sqrt 2}={t-4\over \sqrt{3^2+4^2+(t-4)^2}} \Rightarrow {1\over 2}={(t-4)^2\over t^2-8t+41} \Rightarrow t^2-8t-9=0 \Rightarrow (t-9)(t+1)=0\\ \Rightarrow t=9,-1，故選\bbox[red,2pt]{(B)}$$解答：$$L:{x+1\over 2}= {y+2\over 3} ={z-1\over 6} 的方向向量\vec u=(2,3,6)，若平面E與L不相交\\，則平面E的法向量\vec n與\vec u垂直，即\vec u\cdot \vec n=0，只有(C)與(E)符合要求；\\又P\in L \Rightarrow P(2t-1,3t-2,6t+1)分別代入(C)與(E)\\，可得\cases{P\in(C)\\ P\not \in (E)}，故選\bbox[red,2pt]{(E)}$$解答：$$第一列未改變\Rightarrow a=1 \Rightarrow \begin{bmatrix}1& 2& 1& 8\\ 2& 1& b& 7\\ 3& -5& 4& c \end{bmatrix} \xrightarrow{-2r_1+r_2,-3r_1+r_3}\begin{bmatrix}1& 2& 1& 8\\ 0& -3& b-2& -9\\ 0& -11& 1& c-24 \end{bmatrix} \\ \Rightarrow \cases{{b-2\over -3}=1\\ c-24=-21} \Rightarrow \cases{b=-1\\ c=3} \Rightarrow a+b+c=1-1+3=3，故選\bbox[red,2pt]{(D)}$$解答：$$\det\begin{bmatrix}a& 3 \\ 1& a-2 \end{bmatrix}=0 \Rightarrow a^2-2a-3=0 \Rightarrow \cases{a=3 \Rightarrow \cases{3x+3y= 3\\ x+y=1} \Rightarrow 無限多解\\ a=-1 \Rightarrow \cases{-x+3y=3 \\ x-3y=1} \Rightarrow 無解}，故選\bbox[red,2pt]{(A)}$$解答：$$1={180\over \pi}度\approx 57.3^\circ \Rightarrow \cases{a=\sin 1=\sin 57.3^\circ\\ b= \sin 2=\sin 114.6^\circ =\sin 65.4^\circ \\ c=\sin 3=\sin 171.9^\circ =\sin 8.1^\circ \\ d=\sin 4=\sin 229.2 =-\sin 49.2^\circ\\ e= \sin 5=\sin 286.5^\circ =-\sin 73.5^\circ }\\ \Rightarrow b\gt a\gt c\gt d\gt e，故選\bbox[red,2pt]{(B)}$$解答：$$\log E=11.8+1.5M \Rightarrow \cases{ E\gt 0\\ M越大，則E越大\\圖形為曲線}\quad，只有(B)符合要求，故選\bbox[red,2pt]{(B)}$$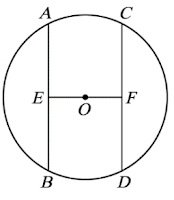解答：$$令\cases{\overline{OE}= \overline{OF}=a \\ \overline{CF}=\overline{DF} =b}，則\cases{a^2+b^2=50^2\\ \overline{AB}+ \overline{CD}+\overline{EF} =2a+4b}\\ 柯西不等式:(a^2+b^2)(2^2+4^2) \ge (2a+4b)^2 \Rightarrow 50^2 \times 20\ge (2a+4b)^2\\ \Rightarrow 2a+4b \le \sqrt{50^2\times 20} =100\sqrt{5}，故選\bbox[red,2pt]{(A)}$$解答：$$平面E的法向量=\overrightarrow{OP} =(3,5,-6)，且O\in E \Rightarrow E:3(x-4)+5(y+2)-6(z-2)=0\\ \Rightarrow 3x+5y-6z+10=0，故選\bbox[red,2pt]{(D)}$$解答：$$({1\over 5})^{20} =0.2^{20}=2^{20}\times 0.1^{20}=1024^2\times 10^{-20} \approx 1000^2\times 10^{-20}=10^{-14}，故選\bbox[red,2pt]{(C)}$$解答：正四體有4個平面，介於平面與頂點中間且與該平面平行的平面，此類平面有四個，如上圖；
正四體有三組歪斜線，與每組歪斜線平行且均分的平面也合乎要求，此類平面有3個；因此共有4+3=7個平面合乎要求，故選\(\bbox[red,2pt]{(D)}\)
二、 多重選擇題（ 40 分）
解答：$$(B)\times: \cases{f_2(0)=1\\ f_2(1)=0.5} \Rightarrow f_2(1)\lt f_2(0)\\ (E)\times: \cases{f_5(\pi/4)= \sin (-{\pi\over 2})=-1 \\f_5(\pi/8)=\sin(-{3\pi\over 4})=-1/\sqrt 2} \Rightarrow f_5(\pi/8) \gt f_5(\pi/4)\\ 其餘皆為遞增函數，故選\bbox[red,2pt]{(ACD)}$$解答：$$(A)\times: \log a+\log b=\log (ab)\ne \log(a+b)\\ (C)\times: {\log_3 2\over \log_3 8} ={\log 2/\log 3\over \log 8/\log 3} ={\log 2\over \log 8} ={\log 2\over 3\log 2}={1\over 3}\ne {1\over 4}\\ (D)\times: 真數需為正數，不存在\log (-2)\\(E)\times: \log 3\lt 0.56 \lt \log 4 \Rightarrow a的最高位數字為3\\，故選\bbox[red,2pt]{(B)}$$解答：$$(A)\bigcirc: \sin \theta \gt 0 \Rightarrow \cases{\theta 在第1象限 \Rightarrow 2\theta 在第2象限 \Rightarrow \sin (2\theta) \gt 0\\ \theta 在第2象限\Rightarrow 2\theta 在第3或第4象限 \Rightarrow \sin (2\theta) \lt 0} \qquad\Rightarrow \theta 在第2象限 \\(B)\bigcirc: \cos(2\theta)=1-2\sin^2\theta=1-2\times {1\over 9}={7\over 9}\\ (C)\times: \sin\theta ={1\over 3} \Rightarrow \cos \theta=-{2\sqrt 2\over 3} \Rightarrow \sin (2\theta)=2\sin \theta \cos\theta =-{4\sqrt 2\over 9} \\\qquad \Rightarrow \tan (2\theta)={\sin(2\theta) \over \cos (2\theta)} ={-4\sqrt 2/9\over 7 /9} = -{4\sqrt 2\over 7} \ne -{4\sqrt 2\over 9}\\(D)\bigcirc: \cos(2\theta+\theta) =\cos(2\theta)\cos\theta- \sin(2\theta)\sin \theta={7\over 9}\cdot {-2\sqrt 2\over 3}-{-4\sqrt 2\over 9} \cdot {1\over 3}=-{10\sqrt 2\over 27} \\(E)\times: \cos \theta=1-2\sin^2{\theta\over 2} \Rightarrow \sin{\theta\over 2}={1\over 2}\sqrt{1-\cos\theta} ={1\over 2}\sqrt{3+2\sqrt 2\over 3} ={1\over 6}\sqrt{9+6\sqrt 2}\\，故選\bbox[red,2pt]{(ABD)}$$解答：$$(A)\bigcirc: 1-{3\over 5} ={2\over 5}\\ (B)\bigcirc: {3\over 5} \times {3\over 5} \times {4\over 5}={36\over 125} \\(C) \times: \cases{鄧射中，其他二人未中:{3\over 5} \times {2\over 5} \times {1\over 5} ={6\over 125} \\ 湯射中，其他二人未中:{2\over 5} \times {3\over 5} \times {1\over 5} ={6\over 125} \\魏射中，其他二人未中:{2\over 5} \times {2\over 5} \times {4\over 5} ={16\over 125} }\\\qquad \Rightarrow 僅一箭射中機率=(6+6+16)/125=28/125 \\(D)\times: {2\over 5} \times {2\over 5} \times {1\over 5} ={4\over 125} =0.032 \gt 0.01\\ (E)\bigcirc: 湯射中，其他二人未中/僅一箭射中={6/125\over 28/125} ={3\over 14}\\，故選\bbox[red,2pt]{(ABE)}$$解答：$$(A)\bigcirc:T=\begin{bmatrix} 1& 0\\0 & 1\end{bmatrix} \Rightarrow \cases{T(A)=A\\ T(B)=B \\T(C)=C} \Rightarrow 頂點位置不變，面積不變\\(B)\bigcirc:T=\begin{bmatrix} 1& 0\\2 & 1\end{bmatrix} \Rightarrow \cases{A'=T(A)=(-1,1)\\ B'=T(B)=(2,8) \\ C'=T(C)=(3,7)} \Rightarrow\cases{\cases{\overrightarrow{AB}=(3,1)\\ \overrightarrow{AC}=(4,-2)} \Rightarrow \begin{Vmatrix}3& 1\\ 4& -2 \end{Vmatrix} =10\\ \cases{\overrightarrow{A'B'}=(3,7) \\ \overrightarrow{A'C'}=(4,6)} \Rightarrow \begin{Vmatrix}3& 7\\ 4& 6 \end{Vmatrix} =10} \\ \qquad \Rightarrow \triangle ABC=\triangle A'B'C' \\(C)\times:T=\begin{bmatrix} 2& 0\\0 & 3\end{bmatrix} \Rightarrow T(x,y)=(2x,3y) \Rightarrow 面積變6倍\\(D)\bigcirc: T=\begin{bmatrix} 1/2& \sqrt 3/2\\\sqrt 3/2 & -1/2\end{bmatrix} = \begin{bmatrix} \cos(2\times 30^\circ) & \sin(2\times 30^\circ)\\ \sin(2\times 30^\circ) & -\cos(2\times 30^\circ)\end{bmatrix}\\\qquad 相當於與斜率為\tan 30^\circ 的直線鏡射，因此面積不變 \\(E)\bigcirc T=\begin{bmatrix} 1/2& -\sqrt 3/2\\\sqrt 3/2 & 1/2\end{bmatrix} = \begin{bmatrix} \cos 60^\circ & -\sin 60^\circ \\ \sin 60^\circ & \cos 60^\circ\end{bmatrix}相當於逆時針旋轉60^\circ，因此面積不變\\，故選\bbox[red,2pt]{(ABDE)}$$
解答：$$(A)\times: (3,3)在y=3^{x-3}+2上，但不在y=\log_3x-2+3上\\(B)\times: (0,0)在y=-2^x+1上，但不在y=-(2^x+1)上\\(C)\bigcirc: \cases{y=x^{\log_4 3} \Rightarrow \log_x y=\log_4 3\\ y=3^{\log_4 x} \Rightarrow \log_3 y=\log_4 x \Rightarrow \log_x y=\log_4 3} \Rightarrow 兩者相同\\(D)\times: \log_4 x^2可以允許x\lt 0，但\log_2 x不允許x\lt 0\\ (E)\bigcirc: \log_2 x為遞增函數\Rightarrow -\log_2 x為遞減\\，故選\bbox[red,2pt]{(CE)}$$解答：$$(A)\times: 見上圖:L在F上且L\parallel E，但E\not \parallel F$$
$$(B)\times:見上圖: L_1\parallel E，但L_2 \not \parallel E\\ ，故選\bbox[red,2pt]{(CDE)}$$
解答：$$(A)\bigcirc: P(A)=0.6 \gt 0.5 \Rightarrow A\cap B= \varnothing \Rightarrow A、B不互斥\\(B)\times: \cases{0.1\le P(A\cap B) \le 0.5\\ P(A)\cdot P(B)=0.6\times 0.5=0.3} \Rightarrow 有可能獨立 \\(C)\times: 0.1\le P(A\cap B) \le 0.5，不一定是0.3\\(D) \times: 200人中有200\times 60\%=120會拉小提琴，因此任選兩人都會拉琴的機率為C^{120}_2/C^{200}_2 \ne 0.36\\(E) \bigcirc:會拉小提琴的人數多於會彈鋼琴\Rightarrow {兩者都會\over 會拉小提琴} \lt {兩者都會\over 會彈鋼琴}\\，故選\bbox[red,2pt]{(AE)}$$
=============== END ========================
解題僅供參考，其他
轉學考試題及詳解
沒有留言:
張貼留言