國立宜蘭大學108學年度暑假轉學招生考試微積分試題
解答：
limt→0tantsec2t3t=limt→0sint3tcostcos(2t)=limt→02sint3t(cos(3t)+cost)=limt→0(2sint)′(3t(cos(3t)+cost))′=limt→02cost3(cos(3t)+cost)−3t(3sin(3t)+sin(t))=26=13，故選(C)解答：
f(x)=x−4x+4=1−8x+4⇒f′(x)=8(x+4)2⇒f′(3)=849，故選(B)解答：
limx→∞3x+2√2x2+1=limx→∞3+2/x√2+1/x2=3√2，故選(C)解答：
f(x)=x3−3x2−24x+2⇒f′(x)=3x2−6x−24⇒f″解答：
g(2)=2^3 = a\cdot 2^2 \Rightarrow a=2，故選\bbox[red, 2pt]{(E)}解答：
\int_0^{\pi/4} \int_0^{\cos \theta} 3r^2 \sin \theta \,drd\theta =\int_0^{\pi/4} \cos^3\theta \sin \theta \,d\theta =\int_1^{\sqrt 2/2} -u^3\,du (取u=\cos\theta \Rightarrow du=-\sin\theta d\theta) \\ =\left.\left[ -{1\over 4}u^4 \right] \right|_1^{\sqrt 2/2} =-{1\over 16}+{1\over 4} ={3\over 16}，故選\bbox[red, 2pt]{(D)}解答：
取\cases{u=x \Rightarrow du=dx\\ dv=e^{-x/2}dx \Rightarrow v=-2e^{-x/2}} \Rightarrow \int_0^4 xe^{-x/2}\,dx = \left.\left[ -2xe^{-x/2} \right]\right|_0^4 +2\int_0^4 e^{-x/2}\,dx\\ =\left.\left[ -2xe^{-x/2} -4e^{-x/2}\right]\right|_0^4 =-12e^{-2}+4，故選\bbox[red, 2pt]{(B)}解答：
取\cases{u=x \Rightarrow du=dx\\ dv=\cos xdx \Rightarrow v=\sin x} \Rightarrow \int_0^{\pi/2} x\cos x\,dx = \left.\left[ x\sin x \right]\right|_0^{\pi/2} -\int_0^{\pi/2} \sin x\,dx\\ =\left.\left[ x\sin x+\cos x\right]\right|_0^{\pi /2} ={\pi \over 2}-1，故選\bbox[red, 2pt]{(C)}解答：
\int_0^2 \int_0^{\sqrt{2x-x^2}} xy\,dydx =\int_0^2 {1\over 2}x(2x-x^2)\,dx =\left.\left[ {1\over 3}x^3 - {1\over 8}x^4\right] \right|_0^2 ={8\over 3}-2={2\over 3}，故選\bbox[red, 2pt]{(D)}解答：
\sum_{n=1}^\infty {2\over 4n^2-1} =\sum_{n=1}^\infty {2\over (2n-1)(2n+1)} =\sum_{n=1}^\infty \left({1\over 2n-1}-{1\over 2n+1} \right)\\ = (1-{1\over 3}) +({1\over 3}-{1\over 5}) +({1\over 5}-{1\over 7}) +\cdots =1，故選\bbox[red, 2pt]{(C)}========================== END ========================
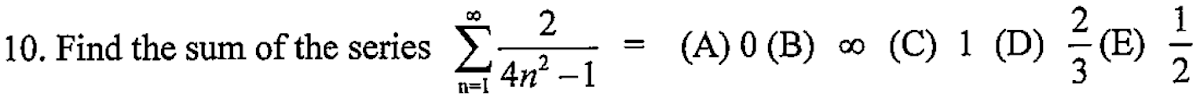
沒有留言:
張貼留言