新北市立國民中學109學年度教師聯合甄選
數學科試題
選擇題: 共 40 題,總分 100 分,每題 2.5 分數學科試題
1. 海拉魯平原上有兩座高塔,高度分別為 15, 20 公尺。現在分別從每一高塔的頂端向對面高塔的底面射出雷射光線,兩光線在空中交於一點。請問該交點距離地面的高度為多少公尺?
(A) 60/7 (B) 9 (C) 100/9 (D) 75/8
解:
$$兩高塔\cases{\overline{AC}=15 \\ \overline{BD}=20},鐳射光交於E,見上圖;\\ \cases{\overline{EF}\parallel \overline{AC} \Rightarrow {h\over 15}={b\over a+b} \\\overline{EF}\parallel \overline{BD} \Rightarrow {h\over 20}={a\over a+b} } \Rightarrow {h\over 15}+{h\over 20}={b\over a+b} +{a\over a+b} =1 \Rightarrow {4h+3h\over 60}=1 \Rightarrow h={60\over 7}\\,故選\bbox[red, 2pt]{(A)}$$
2.坐標平面上,直線\(ax+by+c=0\)不通過第二象限,其中\(a,b,c\)皆為非零常數。則直線\(bx-cy+a=0\)必不通過哪一象限?
(A) 第一象限 (B)第二象限 (C) 第三象限 (D) 第四象限
解:
$$ax+by+c=0不過第2象限 \Rightarrow \cases{斜率:-a/b > 0\\ x截距:-c/a> 0 \\ y截距: -c/b < 0} \\ bx-cy+a=0 \Rightarrow \cases{斜率:b/c > 0\\ x截距:-a/b > 0\\ y截距:a/c < 0} \Rightarrow 不過第2象限\\ 例如:\cases{a=1 \\b=-2\\c=-2} \Rightarrow \cases{x-2y-2=0 不過第2象限\\-2x+2y+1=0不過第2象限 }\\,故選\bbox[red, 2pt]{(B)}$$註:公布的答案是(A)

解:
$$星期日的日期是一奇一偶,也就是本週日是奇數,下周日就是偶數;\\四有30天,最多有5個星期日;因此四月有三個星期日是偶數,\\一定是出現在四月2日,16日,30日; 四月4日在星期二,故選\bbox[red, 2pt]{(B )}$$
解:
$$x^2+y^2=65,x,y\in Z \Rightarrow (x,y)=(\pm 8,\pm 1),(\pm 7, \pm 4),(\pm 4,\pm 7),(\pm 1,\pm 8),共16個,故選\bbox[red, 2pt]{( C)}$$
( A) 21 ( B) 33 ( C) 38 ( D) 44
解:
$$720,840,1080三個數字的最大公因數為120,因此盆栽數量可以是:\\ {720\over 120} +{840\over 120} +{1080\over 120} =,6+7+9=22;或是{720\over 60} +{840\over 60} +{1080\over 60} =12+14+18=44,故選\bbox[red, 2pt]{(D)}$$

解:
$$(B) x^3+3=x^3+(\sqrt[3]{3})^3=(x+\sqrt[3]{3})(x^2-\sqrt[3]{3}x-\sqrt[3]{3})\\ (C)x^4+4 =(x^2)^2+2^2 =(x^2+2)^2-4x^2 =(x^2+2x+2)(x^2-2x+2)\\ (D) x^5+5= x^5+(\sqrt[5]{5})^5 =(x+\sqrt[5]{5})(x^4-\sqrt[5]{5}x^3 +\sqrt[5]{5}x^2-\sqrt[5]{5}x+ 1)\\,故選\bbox[red, 2pt]{(A )}$$
(A) 1/10 (B)1/8 (C) 1/6 (D) 1/4
解:
$$\cases{ax^2+bx+c= a(x+1)(x-6) =ax^2-5ax-6a \\ ax^2+bx+c+1= a(x-1)(x-4) =ax^2-5ax+4a } \\ \Rightarrow -6a+1=4a \Rightarrow a=1/10,故選\bbox[red, 2pt]{(A )}$$

解:
$$2x+3y=0 右移2單位\Rightarrow 2(x-2)+3y=0 \Rightarrow y = -{2\over 3}(x-2),故選\bbox[red, 2pt]{( A)}$$

解:
$$\begin{vmatrix} a & 1 & 1\\ 1 & a & 1\\ 1 & 1 & a\end{vmatrix} =0 \Rightarrow a^3+2-3a=0 \Rightarrow (a-1)^2(a+2)=0\\ 當 a=1,原式\cases{x+y+z=1 \\x+y+z=1\\ x+y+z=1} 有無限多解,故選\bbox[red, 2pt]{( D)}$$
解:
$$先求1\le x\le y \le z\le w\le 10 有 H^{10}_4組;\\再扣除y=z,即1\le x\le y=z\le w\le 10 有 H^{10}_3組,因此共有H^{10}_1-H^{10}_3 =495組,故選\bbox[red, 2pt]{(C)}$$
解:
$$直角\triangle ADC \Rightarrow \overline{AD}^2+\overline{CD}^2= \overline{AC}^2 \Rightarrow \overline{AD}^2+ 25= 169 \Rightarrow \overline{AD}=12\\ \triangle ADC面積= {1\over 2}\overline{AD}\times \overline{DC} = {1\over 2}\overline{AC}\times \overline{DG}\Rightarrow 12\times 5=13\times \overline{DG} \Rightarrow \overline{DG}={60\over 13} \\ 直角\triangle ADG \Rightarrow \overline{AD}^2=\overline{AG}^2+\overline{DG}^2 \Rightarrow 144= \overline{AG}^2+ {3600\over 169} \Rightarrow \overline{AG}={144\over 13}\\
又{\overline{AO} \over \overline{AD}} ={\overline{AE} \over \overline{AG}} \Rightarrow {\overline{AO} \over 12} ={13/2 \over 144/13} \Rightarrow \overline{AO}={169\over 24} \\ I為內心 \Rightarrow \overline{IF}=\overline{ID}= b \Rightarrow {\overline{IF} \over \overline{DG}} ={\overline{AI} \over \overline{AD}} \Rightarrow {b\over 60/13} ={12-b \over 12} \Rightarrow b={10\over 3}\\ \Rightarrow \overline{IO}=\overline{AD}-\overline{AO}-\overline{ID} = 12-{169\over 24}-{10\over 3} = {13\over 8},故選\bbox[red, 2pt]{(C)}$$
又{\overline{AO} \over \overline{AD}} ={\overline{AE} \over \overline{AG}} \Rightarrow {\overline{AO} \over 12} ={13/2 \over 144/13} \Rightarrow \overline{AO}={169\over 24} \\ I為內心 \Rightarrow \overline{IF}=\overline{ID}= b \Rightarrow {\overline{IF} \over \overline{DG}} ={\overline{AI} \over \overline{AD}} \Rightarrow {b\over 60/13} ={12-b \over 12} \Rightarrow b={10\over 3}\\ \Rightarrow \overline{IO}=\overline{AD}-\overline{AO}-\overline{ID} = 12-{169\over 24}-{10\over 3} = {13\over 8},故選\bbox[red, 2pt]{(C)}$$
12. 碳-60 分子是一個非常穩定的化學結構,可以用一個有 60 個頂點的凸多面體來呈現:每一個頂點與另外三個頂點相連,而且每一個頂點是兩個正六邊形與一個正五邊形交會之處。請問這樣的模型中,正六邊形與正五邊形的個數總和為多少?
(A) 26 (B) 28 (C) 30 (D) 32
解:
$$連線數=60\times 3\div 2=90,由尤拉定理: 點-線+面=2 \Rightarrow 60-90+面=2 \Rightarrow 面=32\\,故選\bbox[red, 2pt]{(D)}$$
解:
$${1\over x^3-1} = {a\over x-1}+{bx+c\over x^2+x+1} ={a(x^2+x+1)+(bx+c)(x-1)\over x^3-1} = {(a+b)x^2+(a-b+c)x +a-c\over x^3-1} \\ \Rightarrow \cases{a+b=0 \\ a-b+c=0 \\ a-c=1} \Rightarrow \cases{a=1/3\\ b=-1/3 \\ c=-2/3} \Rightarrow a+b+c=-2/3,故選\bbox[red, 2pt]{( B)}$$
解:
$$\cases{\alpha +\beta=-6 \\ \alpha\beta=3} \Rightarrow \cases{{1\over \alpha+2} +{1\over \beta+2} ={ \alpha+\beta+4\over (\alpha+2) (\beta+2)}={\alpha +\beta+4\over \alpha\beta +2(\alpha+\beta) +4} ={-2\over -5}\\{1\over \alpha+2} \times {1\over \beta+2}={ 1\over (\alpha+2) (\beta+2)} ={1\over \alpha\beta +2(\alpha+\beta) +4}={1\over -5}} \\ \Rightarrow x^2-{2\over 5}x-{1\over 5}=0 \Rightarrow 5x^2-2x-1=0,故選\bbox[red, 2pt]{(A )}$$
解:
$$直線L的斜率為{1\over 3},經過(-1,-2)且斜率為-3的直線方程式: y+2=-3(x+1) \\\Rightarrow 3x+y=-5,故選\bbox[red, 2pt]{(D)}$$
解:
$$A4尺寸:210\times 297 = 62370 \;mm^2=623.7\;cm^2 =0.06237\;m^2\\地圖:35873.196 \;km^2 縮小100\times 100 \Rightarrow 3.5873196\;km^2= 3.5873196\times 10^6 \;m^2\\ {3.5873196\times 10^6 \over 0.06237}\approx 57.5\times 10^6=5.8\times 10^7,故選\bbox[red, 2pt]{( B)}$$
解:
$$令\cases{\triangle ABC三中線長分別為4,6,8\\ \triangle DEF三邊長分別為4,6,8\\S=(4+6+8)\div 2 =9} \Rightarrow \triangle DEF 面積=\sqrt{S(S-4)(S-6)(S-8)} \\ =\sqrt{9\times 5\times 3\times 1} =3\sqrt {15} \Rightarrow \triangle ABC={4\over 3}\triangle DEF = {4\over 3}\times 3\sqrt{15}=4\sqrt {15},故選\bbox[red, 2pt]{( B)}$$註: 三角形三中線所圍面積比例的說明:按這裡
解:
$$|ax+1| \le b \Rightarrow -b \le ax+1 \le b \Rightarrow -b-1 \le ax \le b-1 \Rightarrow \begin{cases} {-b-1\over a}\le x \le {b-1\over a} & 0< a\\ {-b-1\over a}\ge x \ge {b-1\over a} & 0> a \end{cases} \\ \\若a>0,則\cases{{-b-1\over a}=-3\\ {b-1\over a}=5},兩式相加\Rightarrow -2/a=2 \Rightarrow a=-1不合(違反a>0);\\ 若a< 0 \Rightarrow \cases{{-b-1\over a}=5\\ {b-1\over a}=-3} \Rightarrow a=-1 \Rightarrow b=4 \Rightarrow a+b=3,故選\bbox[red, 2pt]{( C)}$$
19. 平平參加丟銅板比賽,持續丟擲一枚均勻銅板,直到出現正面時才停止。若正面出現在第 k 次丟擲,則可得分數 k 分。則平平所得分數的期望值為多少?
(A) 1 (B) 2 (C) 5/2(D) 3
解:
$$S=\sum_{k=1}^\infty {k\over 2^k} = {1\over 2} + {2\over 2^2}+ {3\over 2^3} +\cdots + {n\over 2^n}+\cdots \cdots(1) \\ \Rightarrow {1\over 2}S={1\over 2^2} + {2\over 2^3}+ {3\over 2^4} +\cdots + {n\over 2^{n+1}}+\cdots \cdots(2)\\ (1)-(2) \Rightarrow {1\over 2}S ={1\over 2} + {1\over 2^2}+ {1\over 2^3} +\cdots + {1\over 2^n}+\cdots ={1/2 \over 1-1/2}=1 \\ \Rightarrow S=2,故選\bbox[red, 2pt]{(B )}$$
解:
$$f(x)=x^3+2x^2-4x+2 = (x^2+3x-1)(x-1)+1 =((x+4)(x-1)+3)(x-1)+1 \\ =(((x-1)+5)(x-1)+3)(x-1)+1 = ((x-1)^2+5(x-1)+3)(x-1)+1\\ =(x-1)^3+5(x-1)^2+3(x-1)+1\\ \Rightarrow f(0.9999)=(-0.0001)^3 +5(-0.0001)^2+3(-0.0001)+1 \approx 3(-0.0001)+1 \\ =0.9997,故選\bbox[red, 2pt]{(A )}$$
解:
$$\overline{CD}\bot \overline{AB},故選\bbox[red, 2pt]{(A )}$$
解:
$$\cases{\theta 在第2象限 \\ \cos \theta =-{4\over 5}} \Rightarrow \sin \theta ={3\over 5} \Rightarrow \tan \theta=\cases{\sin\theta /\cos \theta=-3/4 \\ {2\tan (\theta/2) \over 1-\tan^2 (\theta/2)}} \\ \Rightarrow {2\tan (\theta/2) \over 1-\tan^2 (\theta/2)} =-{3\over 4} \Rightarrow (\tan(\theta/2)-3)(3\tan(\theta/2)+1)=0 \Rightarrow \tan(\theta/2) = 3或-1/3\\ 由於 \pi/2 < \theta < \pi \Rightarrow \pi/4 < \theta/2 < \pi/2 \Rightarrow \infty > \tan(\theta/2) >1 \Rightarrow \tan(\theta/2)=3,故選\bbox[red, 2pt]{(A )}$$
解:
$$\cases{(A)6^6=2^6\cdot 3^6 \Rightarrow 正因數總和=(2^0+2^1+\cdots +2^6)(3^0+3^1+\cdots +3^6) = 奇\times 奇=奇\\ (B)7^7 正因數總和= 7^0+7^1+\cdots +7^7 = 8\times 奇=偶\\ (C)8^8 正因數總和= 8^0+8^1+\cdots +8^8 = 1+偶= 奇\\ (D)9^9 正因數總和= 9^0+9^1+\cdots +9^9 = 10\times 奇= 偶}\\,故選\bbox[red, 2pt]{( BD)}$$註:公佈答案為(B)
解:
解:
解:
解:
解:
解:
解:
解:
解:
解:
解:
解:
$$\cases{A(1,2,-1) \\ B(2,-1,2) \\ C(3,2,1) \\ D(-1,-a-1,a)} \Rightarrow \cases{\overrightarrow{AB} =(1,-3,3) \\\overrightarrow{AC} = (2,0,2)} \Rightarrow \vec n=\overrightarrow{AB} \times \overrightarrow{AC} = (-6,4,6) \\ \Rightarrow A,B,C所在的平面E:-6(x-1)+4(y-2)+6(z+1)=0;\\ D在E上\Rightarrow -6\times (-2)+4\times (-a-3) +6\times (a+1)=0 \Rightarrow a=-3,故選\bbox[red, 2pt]{(C )}$$
解:
$$36^{1-\sqrt 2\over \sqrt 2} \times 6^{-\sqrt 2} =6^{2-2\sqrt 2\over \sqrt 2} \times 6^{-\sqrt 2} = 6^{\sqrt 2-2} \times 6^{-\sqrt 2} =6^{\sqrt 2-2-\sqrt 2} =6^{-2} ={1\over 36},故選\bbox[red, 2pt]{(D)}$$
解:
$$f(x)= -x^2+2x+6 =-(x-1)^2+7 \Rightarrow x=1有最大值,但1 \not \in [2,3]\\ 因此挑選該區間離1最近的數,即2 \Rightarrow f(2)=-1+7=6為區間內最大值,故選\bbox[red, 2pt]{(B)}$$
解:
$$假設圓心為O(a,b)\Rightarrow \cases{\overline{OA} =\overline{OC} \\ \overline{OB}=\overline{OC} }\Rightarrow \cases{(a-1)^2 +(b-1)^2 = (a-3)^2+(b-1)^2 \cdots(1) \\ (a-4)^2 +b^2=(a-3)^2+(b-1)^2 \cdots(2)} \\ (1)\Rightarrow -2a+1 =-6a+9 \Rightarrow a=2 代入(2) \Rightarrow 4+b^2 = 1+(b-1)^2 \Rightarrow b=-1 \\ \Rightarrow 圓半徑R =\overline{OB} =\sqrt{(-)2^2 +(-1)^2} \Rightarrow \sqrt 5 \Rightarrow 圓方程式: (x-a)^2 +(y-b)^2=R^2 \\ \Rightarrow (x-2)^2 +(y+1)^2 = 5,故選\bbox[red, 2pt]{( C)}$$
解:
$$圓C: x^2+y^2-2x+4y-4=0 \Rightarrow (x-1)^2 +(y+2)^2 = 3^2;\\ 令 \cases{圓心O(1,-2) \\ 半徑r=3 \\ 割線長=2L} \Rightarrow d=\text{dist}(O,L)= {4-6+7 \over 5}=1 \Rightarrow r^2=d^2+L^2 \Rightarrow 9=1+L^2 \\ \Rightarrow L=2\sqrt 2 \Rightarrow 2L=4\sqrt 2,故選\bbox[red, 2pt]{(D )}$$
解:
$$\cases{ a_1+a_2+a_3 =21 \\ a_2 +a_3+a_4=42} \Rightarrow \cases{a+ar +ar^2=21\cdots(1) \\ ar+ar^2+ar^3=42 \cdots(2)} \Rightarrow {(1)\over (2)}={a(1+r+r^2) \over ar(1+r+r^2)} ={1\over r}={21 \over 42} ={1\over 2} \\ \Rightarrow r=2 代回(1) \Rightarrow a(1+2+2^2)=21 \Rightarrow a=3 \Rightarrow \sum_{n=1}^7 a_n ={a-ar^7\over 1-r} ={ 3(1-2^7)\over 1-2} = 38\\1,故選\bbox[red, 2pt]{(A )}$$
解:
$$1\times 5+ 2\times 9+3\times 13+\cdots+14\times 57 = \sum_{n=1}^{14}n(5+4(n-1)) = \sum_{n=1}^{14}(4n^2+ n) \\ = 4\times {14\times 15\times 29 \over 6} +{14\times 15\over 2} =4060+105 =4165,故選\bbox[red, 2pt]{(B )}$$
解:
$$\cases{A(1,2) \\B(4,6) \\C(3,3)} \Rightarrow \cases{\overrightarrow{AB} =(3,4) \\\overrightarrow{AC} =(2,1)} \Rightarrow 正射影長={\overrightarrow{AB} \cdot \overrightarrow{AC} \over |\overrightarrow{AC}|} ={10\over \sqrt {5}} =2\sqrt 5,故選\bbox[red, 2pt]{(C )}$$
解:
$$\cases{P((紅,藍))={3\over 5} \times {2\over 5} ={6\over 25} \\ P((藍,紅))={2\over 5} \times {3\over 5} ={6\over 25}} \Rightarrow P((紅,藍))+P((藍,紅))= {6\over 25}+{6\over 25}={12\over 25} =0.48,故選\bbox[red, 2pt]{(D )}$$
33. 某工廠生產燈泡,其品檢部門在檢驗燈泡品質時是從每一盒(每盒 12 個)中任取 4 個來檢查,如果有 2 個或 2 個以上是不合格燈泡,則整盒淘汰。 若某一盒燈泡中有 5 個不合格燈泡,則此盒燈泡被品檢部門淘汰的機率為?
(A) 14/33 (B) 17/33 (C) 19/33 (D) 23/33
解:
$${ {5\choose 4} +{5\choose 3}{7\choose 1}+{5\choose 2}{7\choose 2}\over {12 \choose 4}} ={5+10\times 10\times 21 \over 11\times 45} ={19\over 33},故選\bbox[red, 2pt]{( C)}$$
解:
$$-1\le \sin{1\over x} \le 1 \Rightarrow -|x|\le x\sin{1\over x} \le |x| \Rightarrow \lim_{x\to 0}-|x|\le \lim_{x\to 0} x\sin{1\over x} \le \lim_{x\to 0}|x| \\\Rightarrow 0\le \lim_{x\to 0} x\sin{1\over x} \le 0 \Rightarrow \lim_{x\to 0} x\sin{1\over x} =0,故選\bbox[red, 2pt]{( C)}$$
解:
$$2\theta +3\theta +4\theta =180^\circ \Rightarrow \theta =20^\circ \Rightarrow \cos \angle B= \cos 60^\circ = {a^2+c^2-b^2 \over 2ac} ={1\over 2} \Rightarrow \color{blue}{b^2-c^2}=a^2-ac\\ 在\overline{AB}上找一點B',使得\angle CB'B= \angle B=3\theta =60^\circ (見上圖,\triangle CB'B為正\triangle) \Rightarrow \angle ACB'=\theta\\ \Rightarrow \cos \angle ACB' = \cos \theta ={a^2+b^2-(c-a)^2 \over 2ab} = {\color{blue}{b^2-c^2}+2ac \over 2ab} = {a^2-ac+2ac \over 2ab} ={a+c\over 2b} \\ \Rightarrow \sec \theta ={2b\over a+c},故選\bbox[red, 2pt]{(A )}$$
解:
$$\lim_{x\to \pi/2} (\pi-2x)\tan x =\lim_{x\to \pi/2} {(\pi-2x)\sin x\over \cos x} =\lim_{x\to \pi/2} {((\pi-2x)\sin x)'\over (\cos x)'} \\=\lim_{x\to \pi/2} {-2\sin x+(\pi-2x)\cos x\over -\sin x} ={-2+0 \over -1} =2,故選\bbox[red, 2pt]{(D )}$$
解:
$$\log a=1.02 \Rightarrow a=10^{1.02}=10\cdot 10^{0.02} \Rightarrow 10^{0.02}={a\over 10} \\ \Rightarrow 0.01^{0.01} = (10^{-2})^{0.01} =10^{-0.02} =({a\over 10})^{-1}= {10\over a},故選\bbox[red, 2pt]{( D)}$$
解:
$$\sum_{k=1}^9 {2k+1\over k^2(k+1)^2} = \sum_{k=1}^9 \left({1\over k^2}-{1\over (k+1)^2} \right)= {1\over 1^2}-{1\over (9+1)^2} =1-{1\over 100}= {99\over 100},故選\bbox[red, 2pt]{(B )}$$
解:
$${x^2-4x \over x^2-4}+2={1\over 2-x} \Rightarrow {3x^2-4x-8 \over x^2-4} ={1\over 2-x} \Rightarrow (3x^2-4x-8)(2-x) =x^2-4=(x+2) (x-2) \\ \Rightarrow 3x^2-4x-8=-x-2 \Rightarrow 3x^2-3x-6=0 \Rightarrow 3(x-2)(x+1)=0 \\ \Rightarrow x=1 (2不合,分母為0) \Rightarrow 只有1根,故選\bbox[red, 2pt]{( B)}$$
解:
$$\cases{L_1方向向量\stackrel{\rightharpoonup}{u}=(1,2,-2) \\ L_2方向向量\stackrel{\rightharpoonup}{v}=(-3,4,1)} \Rightarrow \stackrel{\rightharpoonup}{n} =\stackrel{\rightharpoonup}{u}\times \stackrel{\rightharpoonup}{v} = (10,5,10)\\ \cases{在L_1上任找一點P(-2,3,-3) \\在L_2上任找一點Q(2,-2,0)} \Rightarrow \overrightarrow{PQ}=(4,-5,3)\\ 本題相當於求\overrightarrow{PQ} 在\vec n上的投影長= {\overrightarrow{PQ} \cdot \vec n \over |\vec n|} ={40-25+30 \over \sqrt{10^2+5^2 +10^2}} ={45 \over 15} =3,故選\bbox[red, 2pt]{(A )}$$
解:
$$,故選\bbox[red, 2pt]{( )}$$
解:
$$,故選\bbox[red, 2pt]{( )}$$
解:
$$,故選\bbox[red, 2pt]{( )}$$
解:
$$,故選\bbox[red, 2pt]{( )}$$
-- END (僅供參考) --
























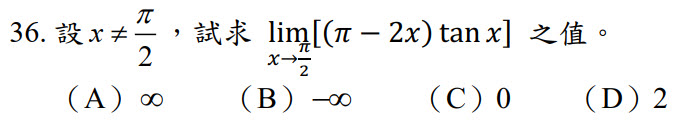




沒有留言:
張貼留言