國立中興大學附屬高級中學106學年度第1次教師甄選
解答:$$\cases{a=\sqrt 3+\sqrt 2\\ b=\sqrt 3-\sqrt 2} \Rightarrow \cases{a^2=5+2\sqrt 6\\ b^2= 5-2\sqrt 6\\ ab=1} \Rightarrow \cases{a^4=49+20\sqrt 6 \\ b^4=49-20\sqrt 6 \\a^2b^2=1}\\ \Rightarrow a^6+b^6 =(a^2)^3+(b^2)^3 =(a^2+b^2)(a^4+b^4-a^2b^2) = 10(98-1) =970 \\ 由於0\lt b^2 \lt 1 \Rightarrow 969\lt a^6 \lt 970 \Rightarrow \lceil a^6 \rceil = \bbox[red,2pt]{970}$$解答:$$\triangle ABC邊長分別\cases{\overline{BC}=a \\ \overline{AC}=a-k \\ \overline{AB}=a-2k} \Rightarrow \cos \angle A=-{1\over 2} = {(a-k)^2+(a-2k)^2 -a^2\over 2(a-k)(a-2k)} \\ \Rightarrow 2a^2-9ak+7k^2=0 \Rightarrow (2a-7k)(a-k)=0 \Rightarrow a={7\over 2}k (a=k \Rightarrow \overline{AC}=a-k=0, 不合)\\ \Rightarrow \cases{\overline{BC}=7k/2 \\ \overline{AC}=5k/2 \\ \overline{AB}=3k/2} \Rightarrow 邊長比=\bbox[red,2pt]{7:5:3}$$
解答:
$$曲線\Gamma:y=2^x上的點A,其坐標可紀錄為A(x,2^x);\\令\cases{P(1,4)\\ Q(2,5)},則\sqrt{4^x-5\times 2^{x+1}+x^2 -4x+29} -\sqrt{4^x -2^{x+3}+x^2-2x+17} \\ =\sqrt{(x-2)^2+(2^x-5)^2} -\sqrt{(x-1)^2 +(2^x-4)^2} = \overline{AQ}- \overline{AP} 最大值=\overline{PQ} = \bbox[red,2pt]{\sqrt{2}}$$
解答:$$\cases{a=\log_3 \sqrt 6 ={1\over 2}(\log_3 3+\log_3 2) ={1\over 2}(1+\log _3 2)\\ b=\sqrt {\log_3 2} \lt 1} \Rightarrow 2a-1=b^2 \Rightarrow a=(b^2+1)/2 \\ \Rightarrow \sqrt{\log_3 \sqrt 6 +\sqrt{\log_3 2}} +\sqrt{\log_3 \sqrt 6 -\sqrt{\log_3 2}} =\sqrt {a+b} -\sqrt{a-b} \\=\sqrt{{b^2+1\over 2}+b} +\sqrt{{b^2+1\over 2}-b} =\sqrt{{1\over 2}(b+1)^2} +\sqrt{{1\over 2}(b-1)^2} ={1\over \sqrt 2}(b+1) +{1\over \sqrt 2}\color{blue}{(1-b)} \\ = {2\over \sqrt 2} =\bbox[red,2pt]{\sqrt{2}}$$
解答:

$$\log_{x+y} \sqrt{1-x^2} \gt \log_{x+y} y \Rightarrow \cases{1-x^2 \gt 0\\ y \gt 0\\ x+y \gt 0\\ \cases{\sqrt{1-x^2} \gt y,\text{ if }x+y \gt 1\\\sqrt{1-x^2} \lt y,\text{ if }x+y \lt 1}} \\\Rightarrow \cases{藍色區域: x+y>1 且 x^2+y^2 < 1\\ 紅色區域:0 < x+y < 1且x^2+y^2 > 1 且x > -1} \\ \Rightarrow \cases{藍色區域面積={\pi\over 4}-{1\over 2} \\ 紅色區域面積= {1\over 2}+ (1-{\pi\over 4})\div 2} \Rightarrow 著色面積=\bbox[red,2pt]{{1\over 2}+{\pi \over 8}}$$
解答:$$令\cases{A(0,0,0)\\ B(6,0,0)\\ C(3,6\sqrt 2,0)\\ O(3,a,b)},則\cases{\overline{OA}=9 \\ \overline{OC}=6} \Rightarrow \cases{\sqrt{9+a^2+b^2} =9\\ \sqrt{(a-6\sqrt 2)^2+b^2}=6} \Rightarrow \cases{a=9/\sqrt 2\\ b=3\sqrt 7 /\sqrt 2} \\ \Rightarrow 四面積O-ABC體積= {1\over 3}\times \triangle ABC 面積\times 高={1\over 3}\times \left({1\over 2}\times 6\times 6\sqrt 2 \right)\times {3\sqrt 7\over \sqrt 2} =\bbox[red,2pt]{18\sqrt 7}$$
解答:$$|z|=1 \Rightarrow z=\cos \theta+i\sin \theta \Rightarrow |z^2-z+1|= |z(z-1+{1\over z})| =|z||z-1+{1\over z}| =|z-1+{1\over z}| \\ =|\cos \theta +i\sin \theta-1+\cos(-\theta)+i\sin(-\theta)|=|2\cos \theta-1|\Rightarrow \begin{cases} 最大值M=3 & \text{if }\cos\theta=-1 \\ 最小值m=0 & \text{if }\cos\theta=1\end{cases}\\ \Rightarrow M+m= \bbox[red,2pt]{3}$$
解答:$$代公式(k-1)^{n}+(-1)^n\times(k-1) = (3-1)^{12}+(-1)^{12}(3-1) = 2^{12}+2= \bbox[red,2pt]{4098}$$
解答:$$圓\cases{x^2+(z-1)^2 =1\\ y=0}上的點P(\cos \theta,0,\sin\theta+1)至Q(0,2,2)的直線可表示成:\\{x\over \cos \theta} ={y-2 \over -2} ={z-2 \over \sin \theta-1} ,則該直線與xy平面(z=0)的交集為{x\over \cos \theta} ={y-2 \over -2} ={-2 \over \sin \theta-1} \\\Rightarrow \cases{-2x=(y-2)\cos \theta\\ (y-2)(\sin \theta-1)=4} \Rightarrow \cases{\cos \theta={-2x\over y-2} \\ \sin\theta = {y+2\over y-2}} \Rightarrow \cos^2 \theta+\sin^2 \theta = {4x^2+(y+2)^2 \over (y-2)^2}=1 \\\Rightarrow \bbox[red,2pt]{x^2+2y=0且z=0}$$
解答:$$f(n)=\sum_{k=1}^n {1\over (2k)(2k-1)} = \sum_{k=1}^n \left({1\over 2k-1}-{1\over 2k} \right)= 1-{1\over 2} +{1\over 3}-{1\over 4}+\cdots +{1\over 2n-1}-{1\over 2n}\\ =\left( 1+{1\over 3} +{1\over 5} +\cdots +{1\over 2n-1}\right) -\left( {1\over 2}+ {1\over 4}+\cdots +{1\over 2n}\right)\\= \left( 1+ {1\over 2}+{1\over 3}+{1\over 4} +{1\over 5} +\cdots +{1\over 2n-1} +{1\over 2n}\right) -2\left( {1\over 2}+ {1\over 4}+\cdots +{1\over 2n}\right)\\= \left( 1+ {1\over 2}+{1\over 3}+{1\over 4} +{1\over 5} +\cdots +{1\over 2n-1} +{1\over 2n}\right) -\left( 1+ {1\over 2} +{1\over 3} +\cdots +{1\over n}\right)\\={1\over n+1} +{1\over n+2} +\cdots +{1\over 2n} =\sum_{k=1}^n {1\over n+k} =\sum_{k=1}^n {1\over n(1+k/n)} \\ \Rightarrow \lim_{n\to\infty} f(n)=\int_0^1 {1\over 1+x}\;dx = \left.\ln (1+x)\right|_0^1 =\bbox[red,2pt]{\ln 2}$$
解答:$$A={1\over 2}\begin{bmatrix}\cos{2\pi\over n} & -\sin {2\pi\over n}\\ \sin{2\pi\over n} & \cos {2\pi\over n}\end{bmatrix} \Rightarrow A^k= {1\over 2^k}\begin{bmatrix}\cos{2k\pi\over n} & -\sin {2k\pi\over n}\\ \sin{2k\pi\over n} & \cos {2k\pi \over n}\end{bmatrix} \\\Rightarrow \cases{P_k=A^{k-1}\left[\matrix{ 1\\ 0}\right] = {1\over 2^{k-1}}\left[\matrix{ \cos{2(k-1)\pi\over n}\\ \sin {2(k-1)\pi\over n}}\right] \\P_{k+1}= A^{k}\left[\matrix{ 1\\ 0}\right] = {1\over 2^{k}}\left[\matrix{ \cos{2k\pi\over n}\\ \sin {2k\pi\over n}}\right]} \Rightarrow S_k={1\over 2}\begin{Vmatrix} {1\over 2^{k-1}} \cos{2(k-1)\pi \over n} & {1\over 2^{k-1}} \sin{2(k-1)\pi \over n} \\ {1\over 2^{k}} \cos{2k\pi \over n} & {1\over 2^{k}} \sin{2k\pi \over n}\end{Vmatrix} \\ ={1\over 2^{2k}}\sin{2\pi\over n} \Rightarrow \lim_{n\to \infty}\left( n\times \sum_{k=1}^n S_k\right) =\lim_{n\to \infty}n\sin{2\pi \over n}({1\over 2^2} +{1\over 2^4} +\cdots +{1\over 2^{2n}} )\\ = 2\pi\lim_{n\to \infty} {\sin 2\pi/n \over 2\pi/n} \times \lim_{n\to \infty}{2^{2n}-1 \over 3\times 2^{2n}} = 2\pi \times {1\over 3} =\bbox[red,2pt]{2\pi \over 3}$$
解答:$$令\cases{a=x \ge 0\\ b=2y\ge 0\\ c=3z\ge 0},則此變為:已知a+b+c=1,求a^2b +b^2c +c^2a的最大值\\ 假設a\ge b\ge c,則\cases{ac \ge bc\\ b\ge c} \Rightarrow abc+bc^2 \ge ac^2+b^2c \text{ (Rearrangement inequality) } \\ \Rightarrow a^2b +b^2c +c^2a \le a^2b+ abc+bc^2 = b(a^2+ac+c^2) \le b(a+c)^2 \le 4\left({{a+c\over 2} +{a+c\over 2} +b \over 3} \right)^3 \\=4({a+b+c \over 3})^3 ={4\over 27} \Rightarrow a^2b +b^2c +c^2a的最大值為\bbox[red,2pt]{4\over 27}$$
解答:$$\angle POQ=90^\circ \Rightarrow {1\over \overline{OP}^2} +{1\over \overline{OQ}^2} ={1\over 3} +{1\over 4}={7\over 12}\\ 因此\cfrac{{1\over \overline{OP}^2} +{1\over \overline{OQ}^2}}{2} \ge \sqrt{{1\over \overline{OP}^2} \times {1\over \overline{OQ}^2}} \Rightarrow {7\over 24} \ge {1\over \overline{OP}\times \overline{OQ}} \Rightarrow \overline{OP}\times \overline{OQ} \ge {24\over 7} \\ \Rightarrow \triangle POQ= {1\over 2}\times \overline{OP}\times \overline{OQ} \ge {12\over 7 } \Rightarrow \triangle POQ面積的最小值=\bbox[red,2pt]{12 \over 7}$$
解答:$$代公式:\cases{C_n=2^{n \choose 2}-{1\over n}\sum_{i=1}^{n-1}i{n \choose i}2^{n-i\choose 2}C_i, \text{ for }n\gt 1\\ C_1=1}\\ \Rightarrow C_2=1 \Rightarrow C_3=4 \Rightarrow C_4=38 \Rightarrow C_5=728 \Rightarrow C_6= \bbox[red,2pt]{26704}$$
解答:$$令\cases{A(0,0,0)\\ B(6,0,0)\\ C(3,6\sqrt 2,0)\\ O(3,a,b)},則\cases{\overline{OA}=9 \\ \overline{OC}=6} \Rightarrow \cases{\sqrt{9+a^2+b^2} =9\\ \sqrt{(a-6\sqrt 2)^2+b^2}=6} \Rightarrow \cases{a=9/\sqrt 2\\ b=3\sqrt 7 /\sqrt 2} \\ \Rightarrow 四面積O-ABC體積= {1\over 3}\times \triangle ABC 面積\times 高={1\over 3}\times \left({1\over 2}\times 6\times 6\sqrt 2 \right)\times {3\sqrt 7\over \sqrt 2} =\bbox[red,2pt]{18\sqrt 7}$$
解答:$$|z|=1 \Rightarrow z=\cos \theta+i\sin \theta \Rightarrow |z^2-z+1|= |z(z-1+{1\over z})| =|z||z-1+{1\over z}| =|z-1+{1\over z}| \\ =|\cos \theta +i\sin \theta-1+\cos(-\theta)+i\sin(-\theta)|=|2\cos \theta-1|\Rightarrow \begin{cases} 最大值M=3 & \text{if }\cos\theta=-1 \\ 最小值m=0 & \text{if }\cos\theta=1\end{cases}\\ \Rightarrow M+m= \bbox[red,2pt]{3}$$
解答:$$代公式(k-1)^{n}+(-1)^n\times(k-1) = (3-1)^{12}+(-1)^{12}(3-1) = 2^{12}+2= \bbox[red,2pt]{4098}$$
解答:$$圓\cases{x^2+(z-1)^2 =1\\ y=0}上的點P(\cos \theta,0,\sin\theta+1)至Q(0,2,2)的直線可表示成:\\{x\over \cos \theta} ={y-2 \over -2} ={z-2 \over \sin \theta-1} ,則該直線與xy平面(z=0)的交集為{x\over \cos \theta} ={y-2 \over -2} ={-2 \over \sin \theta-1} \\\Rightarrow \cases{-2x=(y-2)\cos \theta\\ (y-2)(\sin \theta-1)=4} \Rightarrow \cases{\cos \theta={-2x\over y-2} \\ \sin\theta = {y+2\over y-2}} \Rightarrow \cos^2 \theta+\sin^2 \theta = {4x^2+(y+2)^2 \over (y-2)^2}=1 \\\Rightarrow \bbox[red,2pt]{x^2+2y=0且z=0}$$
解答:$$f(n)=\sum_{k=1}^n {1\over (2k)(2k-1)} = \sum_{k=1}^n \left({1\over 2k-1}-{1\over 2k} \right)= 1-{1\over 2} +{1\over 3}-{1\over 4}+\cdots +{1\over 2n-1}-{1\over 2n}\\ =\left( 1+{1\over 3} +{1\over 5} +\cdots +{1\over 2n-1}\right) -\left( {1\over 2}+ {1\over 4}+\cdots +{1\over 2n}\right)\\= \left( 1+ {1\over 2}+{1\over 3}+{1\over 4} +{1\over 5} +\cdots +{1\over 2n-1} +{1\over 2n}\right) -2\left( {1\over 2}+ {1\over 4}+\cdots +{1\over 2n}\right)\\= \left( 1+ {1\over 2}+{1\over 3}+{1\over 4} +{1\over 5} +\cdots +{1\over 2n-1} +{1\over 2n}\right) -\left( 1+ {1\over 2} +{1\over 3} +\cdots +{1\over n}\right)\\={1\over n+1} +{1\over n+2} +\cdots +{1\over 2n} =\sum_{k=1}^n {1\over n+k} =\sum_{k=1}^n {1\over n(1+k/n)} \\ \Rightarrow \lim_{n\to\infty} f(n)=\int_0^1 {1\over 1+x}\;dx = \left.\ln (1+x)\right|_0^1 =\bbox[red,2pt]{\ln 2}$$
解答:$$A={1\over 2}\begin{bmatrix}\cos{2\pi\over n} & -\sin {2\pi\over n}\\ \sin{2\pi\over n} & \cos {2\pi\over n}\end{bmatrix} \Rightarrow A^k= {1\over 2^k}\begin{bmatrix}\cos{2k\pi\over n} & -\sin {2k\pi\over n}\\ \sin{2k\pi\over n} & \cos {2k\pi \over n}\end{bmatrix} \\\Rightarrow \cases{P_k=A^{k-1}\left[\matrix{ 1\\ 0}\right] = {1\over 2^{k-1}}\left[\matrix{ \cos{2(k-1)\pi\over n}\\ \sin {2(k-1)\pi\over n}}\right] \\P_{k+1}= A^{k}\left[\matrix{ 1\\ 0}\right] = {1\over 2^{k}}\left[\matrix{ \cos{2k\pi\over n}\\ \sin {2k\pi\over n}}\right]} \Rightarrow S_k={1\over 2}\begin{Vmatrix} {1\over 2^{k-1}} \cos{2(k-1)\pi \over n} & {1\over 2^{k-1}} \sin{2(k-1)\pi \over n} \\ {1\over 2^{k}} \cos{2k\pi \over n} & {1\over 2^{k}} \sin{2k\pi \over n}\end{Vmatrix} \\ ={1\over 2^{2k}}\sin{2\pi\over n} \Rightarrow \lim_{n\to \infty}\left( n\times \sum_{k=1}^n S_k\right) =\lim_{n\to \infty}n\sin{2\pi \over n}({1\over 2^2} +{1\over 2^4} +\cdots +{1\over 2^{2n}} )\\ = 2\pi\lim_{n\to \infty} {\sin 2\pi/n \over 2\pi/n} \times \lim_{n\to \infty}{2^{2n}-1 \over 3\times 2^{2n}} = 2\pi \times {1\over 3} =\bbox[red,2pt]{2\pi \over 3}$$
解答:$$令\cases{a=x \ge 0\\ b=2y\ge 0\\ c=3z\ge 0},則此變為:已知a+b+c=1,求a^2b +b^2c +c^2a的最大值\\ 假設a\ge b\ge c,則\cases{ac \ge bc\\ b\ge c} \Rightarrow abc+bc^2 \ge ac^2+b^2c \text{ (Rearrangement inequality) } \\ \Rightarrow a^2b +b^2c +c^2a \le a^2b+ abc+bc^2 = b(a^2+ac+c^2) \le b(a+c)^2 \le 4\left({{a+c\over 2} +{a+c\over 2} +b \over 3} \right)^3 \\=4({a+b+c \over 3})^3 ={4\over 27} \Rightarrow a^2b +b^2c +c^2a的最大值為\bbox[red,2pt]{4\over 27}$$
解答:
$$假設\cases{f(x)=cx(1-x)\\ g(x)=x\\ \Omega_1(綠色區域)= y=f(x)與y=g(x)所圍區域面積 };\\先求兩圖形交點,即cx(1-x)=x \Rightarrow cx^2+(1-c)x=0 \Rightarrow x(cx+1-c)=0 \Rightarrow x=0,1-{1\over c}\\ 令交點\cases{O(0,0)\\ A(1-{1\over c},1-{1\over c})} \Rightarrow \cases{\Omega_1=\int_0^{1-1/c} f(x)-g(x)\;dx ={1\over 2}(1-{1\over c})^2(c-1)-{1\over 3}c(1-{1\over c})^3\\\Omega_c= \int_{0}^1 f(x)\;dx ={1\over 6}c}\\ \Omega_1= {1\over 2}\Omega_c \Rightarrow {1\over 2}(1-{1\over c})^2(c-1)-{1\over 3}c(1-{1\over c})^3={c\over 12} \Rightarrow {1\over 2}(1-{1\over c})^3 -{1\over 3}(1-{1\over c})^3={1\over 12} \\ \Rightarrow {1\over 6}(1-{1\over c})^3 ={1\over 12} \Rightarrow (1-{1\over c})^3 ={1\over 2} \Rightarrow 1-{1\over c}={1\over \sqrt[3] 2} \Rightarrow {\sqrt[3]2-1\over \sqrt[3] 2} ={1\over c} \Rightarrow c=\bbox[red,2pt]{\sqrt[3] 2\over \sqrt[3]2 -1}$$
解答:$$\angle POQ=90^\circ \Rightarrow {1\over \overline{OP}^2} +{1\over \overline{OQ}^2} ={1\over 3} +{1\over 4}={7\over 12}\\ 因此\cfrac{{1\over \overline{OP}^2} +{1\over \overline{OQ}^2}}{2} \ge \sqrt{{1\over \overline{OP}^2} \times {1\over \overline{OQ}^2}} \Rightarrow {7\over 24} \ge {1\over \overline{OP}\times \overline{OQ}} \Rightarrow \overline{OP}\times \overline{OQ} \ge {24\over 7} \\ \Rightarrow \triangle POQ= {1\over 2}\times \overline{OP}\times \overline{OQ} \ge {12\over 7 } \Rightarrow \triangle POQ面積的最小值=\bbox[red,2pt]{12 \over 7}$$
解答:$$代公式:\cases{C_n=2^{n \choose 2}-{1\over n}\sum_{i=1}^{n-1}i{n \choose i}2^{n-i\choose 2}C_i, \text{ for }n\gt 1\\ C_1=1}\\ \Rightarrow C_2=1 \Rightarrow C_3=4 \Rightarrow C_4=38 \Rightarrow C_5=728 \Rightarrow C_6= \bbox[red,2pt]{26704}$$
註: 公式來源\(\href{https://books.google.si/books?id=yJIMx9nXB6kC&pg=PA580&lpg=PA580&dq=number%20of%20simple%20connected%20labeled%20graphs&source=bl&ots=1Reo0hpaQX&sig=0ljeS2CZl3kDDi81jML-SC7jEx4&hl=en&sa=X&ei=YoOSVPjnLIWGzAO7tYDQAg&ved=0CDcQ6AEwBw#v=onepage&q=number%20of%20simple%20connected%20labeled%20graphs&f=false}{按這裡}\)




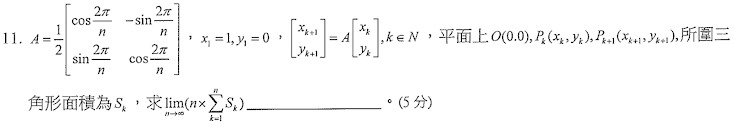




你好:請問第14題的第1行是為什麼呢?謝謝
回覆刪除這是某個定理: 橢圓上兩點P,Q, 若OP垂直OQ則 1/(OP)^2+ 1/(OQ)^2=1/a^2 +1/b^2
刪除