109年特種考試地方政府公務人員考試試題
等 別:三等考試類 科:電力工程、電子工程
科 目:工程數學
甲、申論題部分:(50%)
解:
(一)$$e^{iz} =\cos z+i\sin z \Rightarrow \cos z= {1\over 2}(e^{iz}+e^{-iz})\\ 令\omega=e^{iz},則\cos z=\sqrt 2 \Rightarrow {1\over 2}(\omega+{1\over \omega})=\sqrt 2 \Rightarrow \omega^2-2\sqrt 2\omega+1 =0 \Rightarrow \omega = {\sqrt 2\pm 1} \\ \Rightarrow e^{iz}=\sqrt 2\pm 1 \Rightarrow iz = \ln(\sqrt 2\pm 1) \Rightarrow z= -i\ln(\sqrt 2\pm 1) \Rightarrow \bbox[red, 2pt]{z=-i\ln(\sqrt 2\pm 1)+2n\pi,n\in Z}$$(二)$$f(z)={z^3+z^2 +4\over z^4+4z^2} ={z^3+z^2 +4\over z^2(z+2i)(z-2i)} \Rightarrow \cases{z=0,\pm 2i皆在圓內\\ z=0為二階極點 \\ z=\pm 2i皆為一階極點} \\ \Rightarrow \cases{\text{Res}(f,0)= \left .{d\over dz}(z^2f(z)) \right|_{z=0}= \left.{d\over dz}\left({z^3+z^2 +4\over z^2+4}\right) \right|_{z=0}= \left.{3z^2+2z \over z^2+4}-{2z(z^3+z^2 +4)\over (z^2+4)^2} \right|_{z=0} ={1\over 4} \\\text{Res}(f,2i)= \left.(z-2i)f(z)\right|_{z=2i} = \left.{z^3+z^2 +4\over z^2(z+2i)} \right|_{z=2i}={1\over 2} \\\text{Res}(f,-2i)= \left.(z+2i)f(z)\right|_{z=-2i} = \left.{z^3+z^2 +4\over z^2(z-2i)} \right|_{z=-2i}={1\over 2}}\\ \Rightarrow \oint_C f(z)\;dz = 2\pi i(\text{Res}(f,0)+\text{Res}(f,2i)+ \text{Res}(f,-2i))=2\pi i \times {5\over 4} =\bbox[red,2pt]{{5\over 2}\pi i}$$
解:
解:(一)$$y'(t)+ 5y(t)= 5x(t) =3e^{-2t}u(t) \Rightarrow L\{y'\}+ 5L\{y\} =3L\{e^{-2t}u(t)\} \\ \Rightarrow sY(s)-y(0)+5Y(s) ={3\over s+2} \Rightarrow Y(s)={1\over s+2} -{3\over s+3} \\ \Rightarrow L^{-1}\{ Y(s)\} =L^{-1}\{{1\over s+2} \}- 3L^{-1}\{{1 \over s+3} \} \Rightarrow \bbox[red,2pt]{y(t) =e^{-2t}- 3e^{-3t}}$$(二)$$\text{initial value } x(0) = \lim_{s\to \infty}sX(s) = \lim_{s\to \infty}e^{-2s}{2s^2+1\over (s+2)^2} =0\\ \text{final value } x(\infty) = \lim_{s\to 0}sX(s)= \lim_{s\to 0}e^{-2s}{2s^2+1\over (s+2)^2} = {1\over 4} \\ \Rightarrow \bbox[red, 2pt]{\cases{x(t)的初值為0\\ x(t)的終值為1/4}}$$
解:
(一)(a)$${\bf Ax=b},定義A'=(A|b) =\left(\begin{array}{cccc|c}1 & 2 & 3 & 1 & 3 \\ 3 & 2 & 1 & 4& 6\\ 2 & 6 & 10 & 3 & 6 \\ 1 & 1& 1& 1& k\end{array} \right)\\ \xrightarrow{-r_4+r_1,-3r_4+r_2,-2r_4+r_3}\left(\begin{array}{cccc|c}0 & 1 & 2 & 0 & 3-k \\ 0 & -1 & -2 & 1& 6-3k\\ 0 & 4 & 8 & 1 & 6-2k \\ 1 & 1& 1& 1& k\end{array} \right) \xrightarrow{r_1+r_2,-4r_1+r_3} \left(\begin{array}{cccc|c}0 & 1 & 2 & 0 & 3-k \\ 0 & 0 & 0 & 1& 9-4k\\ 0 & 0 & 0 & 1 & -6+2k \\ 1 & 1& 1& 1& k\end{array} \right) \\ \Rightarrow 9-4k=-6+2k \Rightarrow \bbox[red,2pt]{k={5\over 2}}$$(一)(b)
由(a)可知 \(rank(A)\ne 4 \Rightarrow det(A)=\bbox[red,2pt]{0}\)
(二)$$\cases{{dx_1\over dt}=2x_1-2x_2+3x_3\\ {dx_2\over dt}=x_1+x_2+x_3\\ {dx_3\over dt}=x_1+3x_2-x_3} \Rightarrow \begin{bmatrix}x_1'\\ x_2' \\ x_3' \end{bmatrix} =\begin{bmatrix}2 &-2 & 3\\ 1& 1 & 1 \\ 1 & 3& -1 \end{bmatrix}\begin{bmatrix}x_1\\ x_2 \\ x_3 \end{bmatrix} \\ 令A= \begin{bmatrix}2 &-2 & 3\\ 1& 1 & 1 \\ 1 & 3& -1 \end{bmatrix},\det(A-\lambda I)=0 \Rightarrow \begin{vmatrix}2-\lambda &-2 & 3\\ 1& 1-\lambda & 1 \\ 1 & 3& -1-\lambda \end{vmatrix}=0 \\ \Rightarrow -(\lambda-1)(\lambda+2)(\lambda-3)=0 \Rightarrow \lambda=1,-2,3\\ \lambda=1 \Rightarrow 特徵向量u_1=\begin{bmatrix}-1\\ 1 \\ 1 \end{bmatrix},\lambda=-2 \Rightarrow 特徵向量u_2=\begin{bmatrix}11\\ 1 \\ -14 \end{bmatrix},\lambda=3 \Rightarrow 特徵向量u_3=\begin{bmatrix}1\\ 1 \\ 1\end{bmatrix}\\ \Rightarrow \begin{bmatrix}x_1\\ x_2 \\ x_3\end{bmatrix} = C_1\begin{bmatrix}-1\\ 1 \\ 1 \end{bmatrix}e^x +C_2\begin{bmatrix}11\\ 1 \\ -14 \end{bmatrix}e^{-2x} +C_3\begin{bmatrix}1\\ 1 \\ 1 \end{bmatrix}e^{3x}\\ 將初始值\cases{x_1(0)=1\\ x_2(0)=0 \\ x_3(0)=1/2} 帶入上式\Rightarrow \cases{1=-C_1+11C_2+C_3 \\ 0=C_1+C_2 +C_3\\ 1/2=C_1-14C_2+C_3} \Rightarrow \cases{C_1=-2/3 \\ C_2=-1/30\\ C_3=7/10} \\ \Rightarrow \bbox[red,2pt]{\cases{x_1={2\over 3}e^x -{11\over 30}e^{-2x} +{7\over 10}e^{3x}\\ x_2=-{2\over 3}e^x -{1\over 30}e^{-2x} +{7\over 10}e^{3x}\\ x_3=-{2\over 3}e^x +{14\over 30}e^{-2x} +{7\over 10}e^{3x}}}$$
乙、測驗題部分:(50%)
解:$$\det(A-\lambda I)=0 \Rightarrow \begin{vmatrix} 1-\lambda & 0 & 2\\ 0 & -\lambda & 0 \\ 2 & 0 & 4-\lambda\end{vmatrix}=0 \Rightarrow -\lambda(\lambda-4)(\lambda-1)+4\lambda=0 \\ \Rightarrow -\lambda(\lambda^2-5\lambda+4-4)=0 \Rightarrow -\lambda^2(\lambda-5)=0 \Rightarrow \lambda=0,0,5 \\ \Rightarrow D=\begin{pmatrix} \lambda_1 & 0 & 0\\ 0 & \lambda_2 & 0 \\ 0 & 0 & \lambda_3 \end{pmatrix} =\begin{pmatrix} 0 & 0 & 0\\ 0 & 0 & 0 \\ 0 & 0 & 5 \end{pmatrix}\Rightarrow 故選\bbox[red,2pt]{(A)}$$
解:$$\cases{\det(A)=6\\ \det(B)=2} \Rightarrow \det(AB^{-1}) = \det(A)\cdot \det(B^{-1}) ={\det(A)\over \det(B)} = {6\over 2} =3,故選\bbox[red, 2pt]{(C)}$$
解:$$(A)\bigcirc: \nabla\cdot {\bf r} =({\partial \over \partial x}{\bf i}+ {\partial \over \partial y}{\bf j}+{\partial \over \partial z}{\bf k}) \cdot (x {\bf i} +y{\bf j}+ z{\bf k}) = {\partial \over \partial x}x+ {\partial \over \partial y}y+ {\partial \over \partial z}z =1+1+1=3 \\(B)\bigcirc: \cases{{\bf r}=(x {\bf i} +y{\bf j}+ z{\bf k})\\ {\bf a}=(c_1 {\bf i} +c_2{\bf j}+ c_3{\bf k})} \Rightarrow {\bf a}\times {\bf r} =((c_2z-c_3y){\bf i} +(c_3x-c_1z){\bf j} +(c_1y-c_2x){\bf k}) \\ \qquad \Rightarrow \nabla\cdot ({\bf a}\times {\bf r})= {\partial \over \partial x}(c_2z-c_3y) + {\partial \over \partial y}(c_3x-c_1z) +{\partial \over \partial z}(c_1y-c_2x)=0+0+0 =0\\ (C)\bigcirc: \nabla \times {\bf r} =(({\partial \over \partial y}z-{\partial \over \partial z}y) {\bf i},({\partial \over \partial z}x-{\partial \over \partial x}z) {\bf j}, ({\partial \over \partial x}y-{\partial \over \partial y}x){\bf k})=0 \\ (D)\times: \nabla \times ({\bf a}\times {\bf r}) =\nabla \times ((c_2z-c_3y){\bf i} +(c_3x-c_1z){\bf j} +(c_1y-c_2x){\bf k}) \\ \qquad =(c_1-c_1){\bf i}+ (c_2-c_2){\bf j}+(c_3-c_3){\bf k}=0 \ne {\bf a}\\故選\bbox[red, 2pt]{(D)}$$
解:$$\int_{(1,1)}^{(2,4)}2xy\;dx+x^2\;dy =\left. \left[ x^2y\right] \right|_{(1,1)}^{(2,4)} =16-1=15,故選\bbox[red, 2pt]{(B)}$$
解:$$A=\begin{pmatrix} 1 & 0 \\ 0 & -1\end{pmatrix} \Rightarrow At=\begin{pmatrix} t & 0 \\ 0 & -t\end{pmatrix} \Rightarrow e^{At}= \begin{pmatrix} e^{t} & 0 \\ 0 & e^{-t}\end{pmatrix},故選\bbox[red, 2pt]{(C)}$$
解:
解:$$令\cases{M(x,y)=x+y\\ N(x,y)=x\ln(x)}\\(A)\times: \cases{{\partial \over \partial y}xM = {\partial \over \partial y}(x^2+xy) = x\\{\partial \over \partial x}xN ={\partial \over \partial x}(x^2\ln(x))= 2x\ln(x)+x } \Rightarrow {\partial \over \partial y}xM \ne {\partial \over \partial x}xN \\(B) \times: \cases{{\partial \over \partial y}3M = {\partial \over \partial y}(3x +3y) = 3\\{\partial \over \partial x}3N ={\partial \over \partial x}(3x\ln(x))= 3\ln(x)+3 } \Rightarrow {\partial \over \partial y}3M \ne {\partial \over \partial x}3N \\(C)\bigcirc: \cases{{\partial \over \partial y}{1\over x}M = {\partial \over \partial y}(1 +{y\over x}) = {1\over x}\\{\partial \over \partial x}{1\over x}N ={\partial \over \partial x}\ln(x)= {1\over x} } \Rightarrow {\partial \over \partial y}{1\over x}M = {\partial \over \partial x}{1\over x}N \\(D)\times: \cases{{\partial \over \partial y}{1\over x^2}M = {\partial \over \partial y}({1\over x} +{y\over x^2}) = {1\over x^2}\\{\partial \over \partial x}{1\over x^2}N ={\partial \over \partial x}{\ln(x) \over x}= -{\ln(x)\over x^2}+{1\over x^2} } \Rightarrow {\partial \over \partial y}{1\over x^2}M \ne {\partial \over \partial x}{1\over x^2}N\\ ,故選\bbox[red,2pt]{(C)}$$
解:$$y''-6y'+9y = t^2e^{3t} \Rightarrow L\{y''\}-6L\{y'\}+9L\{y\} =L\{t^2e^{3t}\}\\ \Rightarrow s^2Y(s)-sy(0)-y'(0)-6(sY(s)-y(0))+ 9Y(s)= \frac{2!}{(s-3)^{3}} \\ \Rightarrow s^2Y(s)-2s-6-6sY(s)+12+9Y(s)= \frac{2}{(s-3)^{3}} \\ \Rightarrow Y(s)= {2\over (s-3)^5}+{2 \over s-3 } ={2(s-3)^4+2\over (s-3)^5} ={2(s-c)^d+2 \over (s-a)^b} \Rightarrow \cases{a=3\\ b=5\\ c=3 \\ d=4} \\ \Rightarrow \cases{a+b+c+d =15 \\a+b+c-d= 7 \\a-b-c+d =-1 \\ -a+b-c+d =3 \ne -3},故選\bbox[red,2pt]{(D)}$$
解:$$f(x)=x^3 \Rightarrow f(x)為奇函數\Rightarrow a_0=0,a_n=0,故選\bbox[red,2pt]{(A)}$$
解:$$y=c_1e^x +c_2e^{-2x}+c_3xe^{-2x} \Rightarrow 1, -2,-2為\lambda^2 +a\lambda^2 +b\lambda+c=0之三根為\\ \Rightarrow \cases{a=-(1-2-2) =3\\ b=1\cdot(-2)+ (-2)\cdot (-2)+ (-2)\cdot 1=0\\ c=-1\cdot (-2)\cdot (-2)=-4} \Rightarrow a+b+c=-1,故選\bbox[red,2pt]{(D)}$$
解:$$f(t)=\cos t +\int_0^t e^{-\tau}f(t-\tau)\;d\tau \Rightarrow L\{f(t)\} = L\{\cos t\} +L\{\int_0^t e^{-\tau}f(t-\tau)\;d\tau\} \\ \Rightarrow F(s)={s\over s^2+1} +{F(s)\over s+1} \Rightarrow F(s)={s+1\over s^2+1} ={s\over s^2+1} +{1\over s^2+1} \\ \Rightarrow L^{-1}\{F(s)\}= L^{-1}\{{s\over s^2+1}\}+L^{-1}\{{1\over s^2+1}\} \Rightarrow f(t) =\cos t+\sin t,故選\bbox[red,2pt]{(D)}$$
解:$$f為機率密度函數\Rightarrow \int_{-\infty}^\infty f(x)\;dx=1 \Rightarrow \int_{0}^1 kx^2\;dx =1 \Rightarrow \left. \left[ {1\over 3}kx^3 \right] \right|_{0}^1=1 \Rightarrow {1\over 3}k=1 \Rightarrow k=3\\ \Rightarrow \cases{EX = \int_0^1 xf(x)\;dx =\int_0^1 3x^3\;dx = {3\over 4}\\ EX^2 =\int_0^1 x^2f(x)\;dx = \int_0^13x^4\;dx = {3\over 5}} \Rightarrow \sigma^2 = EX^2-(EX)^2 = {3\over 5} -{9\over 16}= {3\over 80}\\,故選\bbox[red,2pt]{(D)}$$
解:$$ \iint fdxdy=1 \Rightarrow \int_0^1 \int_0^1 kxy \;dxdy =1 \Rightarrow \int_0^1 {1\over 2}ky\;dy =1 \Rightarrow {1\over 4}k = 1 \Rightarrow k=4;\\ 因此P(X>0.25,Y>0.5) = \int_{0.25}^1 \int_{0.5}^1 4xy\;dydx =\int_{0.25}^1 {3\over 2}x\;dx = {45 \over 64},故選\bbox[red, 2pt]{(C)}$$
解:$$z_0=\pi不在圓周|z|=3內,而z_0=\pi/2則在圓周|z|=3內,\\因此\oint_C\left({\cosh z\over (z-\pi)^3} -{\sin^2 z\over (2z-\pi)^3} \right)dz =\oint_C\left( -{\sin^2 z\over (2z-\pi)^3} \right)dz =\oint_C\left( -{\sin^2 z\over 8(z-\pi/2)^3} \right)dz \\=\oint_C {f(z)\over (z-\pi/2)^3} dz , 其中f(z)=-{1\over 8}\sin^2 z \Rightarrow f'(z)=-{1\over 4}\sin z\cos z =-{1\over 8} \sin (2z) \\\Rightarrow f''(z)= -{1\over 4}\cos (2z) \Rightarrow f''(\pi/2)=-{1\over 4}\cos \pi={1\over 4} \\\Rightarrow \oint_C {f(z)\over (z-\pi/2)^3} dz =(2\pi i)\times {1\over 2!}\times f''(\pi/2) = {\pi i\over 4},故選\bbox[red, 2pt]{(A)}$$
解:$${z\over (z+1)(z^2+1)}={z\over (z+1)(z+i)(z-i)} ={f(z)\over z-i} ={g(z)\over z+i},其中\cases{f(z)={z\over (z+1)(z+i) }\\ g(z)={z\over (z+1) (z-i)}}\\ -1不再橢圓內,而\pm i在橢圓內,因此\oint_C{z\over (z+1)(z^2+1)}\;dz = 2\pi i(f(i)+g(-i)) \\=2\pi i({i\over (1+i)(2i)} +{-i\over (1-i)(-2i)}) =2\pi i({1-i\over 4} +{1+i\over 4}) =\pi i,故選\bbox[red, 2pt]{(C)}$$
解:$$z_0={1+i\over \sqrt 2} =\cos {\pi \over 4}+i\sin {\pi \over 4} =e^{i{\pi\over 4}} \Rightarrow \cases{z_0^2 =i\\z_0^4=-1\\ z_0^8=1} \\ \Rightarrow f(z_0) =z_0^{24}- 3z_0^{20}+4z_0^{12}-5z_0^6 =(z_0^{8})^3- 3(z_0^{4})^5+4(z_0^{4})^3-5z_0^4\cdot z_0^2\\ = 1+3-4+5i=5i,故選\bbox[red, 2pt]{(A)}$$
解:$$\oint_\Gamma {\cos (z)\over z}\;dz = \oint_\Gamma {f(z)\over z}\;dz = 2\pi i\times f(0)=2\pi i\times 1 =2\pi i,故選\bbox[red, 2pt]{(D)}$$
解:封閉路徑之線積分為0,故選\(\bbox[red, 2pt]{(C)}\)
解:$$\cases{x=t^2\\ y=-t \\ z=t^2} \Rightarrow \cases{dx=2tdt\\ dy=-dt \\ dz=2tdt} \Rightarrow \int_C x^2dx-yzdy +e^zdz =\int_0^1 t^4(2tdt)-(-t^3)(-dt)+e^{t^2}(2tdt)\\ =\int_0^1 2t^5-t^3+2te^{t^2}\;dt = \left. \left[ {1\over 3}t^6-{1\over 4}t^4+e^{t^2}\right] \right|_0^1 =({1\over 12}+e)-1=e-{11\over 12},故選\bbox[red, 2pt]{(C)}$$
解:$$\det(A-\lambda I)=0 \Rightarrow \begin{vmatrix} 1-\lambda & 0 & 2\\ 0 & -\lambda & 0 \\ 2 & 0 & 4-\lambda\end{vmatrix}=0 \Rightarrow -\lambda(\lambda-4)(\lambda-1)+4\lambda=0 \\ \Rightarrow -\lambda(\lambda^2-5\lambda+4-4)=0 \Rightarrow -\lambda^2(\lambda-5)=0 \Rightarrow \lambda=0,0,5 \\ \Rightarrow D=\begin{pmatrix} \lambda_1 & 0 & 0\\ 0 & \lambda_2 & 0 \\ 0 & 0 & \lambda_3 \end{pmatrix} =\begin{pmatrix} 0 & 0 & 0\\ 0 & 0 & 0 \\ 0 & 0 & 5 \end{pmatrix}\Rightarrow 故選\bbox[red,2pt]{(A)}$$
解:$$\cases{\det(A)=6\\ \det(B)=2} \Rightarrow \det(AB^{-1}) = \det(A)\cdot \det(B^{-1}) ={\det(A)\over \det(B)} = {6\over 2} =3,故選\bbox[red, 2pt]{(C)}$$
解:$$(A)\bigcirc: \nabla\cdot {\bf r} =({\partial \over \partial x}{\bf i}+ {\partial \over \partial y}{\bf j}+{\partial \over \partial z}{\bf k}) \cdot (x {\bf i} +y{\bf j}+ z{\bf k}) = {\partial \over \partial x}x+ {\partial \over \partial y}y+ {\partial \over \partial z}z =1+1+1=3 \\(B)\bigcirc: \cases{{\bf r}=(x {\bf i} +y{\bf j}+ z{\bf k})\\ {\bf a}=(c_1 {\bf i} +c_2{\bf j}+ c_3{\bf k})} \Rightarrow {\bf a}\times {\bf r} =((c_2z-c_3y){\bf i} +(c_3x-c_1z){\bf j} +(c_1y-c_2x){\bf k}) \\ \qquad \Rightarrow \nabla\cdot ({\bf a}\times {\bf r})= {\partial \over \partial x}(c_2z-c_3y) + {\partial \over \partial y}(c_3x-c_1z) +{\partial \over \partial z}(c_1y-c_2x)=0+0+0 =0\\ (C)\bigcirc: \nabla \times {\bf r} =(({\partial \over \partial y}z-{\partial \over \partial z}y) {\bf i},({\partial \over \partial z}x-{\partial \over \partial x}z) {\bf j}, ({\partial \over \partial x}y-{\partial \over \partial y}x){\bf k})=0 \\ (D)\times: \nabla \times ({\bf a}\times {\bf r}) =\nabla \times ((c_2z-c_3y){\bf i} +(c_3x-c_1z){\bf j} +(c_1y-c_2x){\bf k}) \\ \qquad =(c_1-c_1){\bf i}+ (c_2-c_2){\bf j}+(c_3-c_3){\bf k}=0 \ne {\bf a}\\故選\bbox[red, 2pt]{(D)}$$
解:$$\int_{(1,1)}^{(2,4)}2xy\;dx+x^2\;dy =\left. \left[ x^2y\right] \right|_{(1,1)}^{(2,4)} =16-1=15,故選\bbox[red, 2pt]{(B)}$$
解:$$A=\begin{pmatrix} 1 & 0 \\ 0 & -1\end{pmatrix} \Rightarrow At=\begin{pmatrix} t & 0 \\ 0 & -t\end{pmatrix} \Rightarrow e^{At}= \begin{pmatrix} e^{t} & 0 \\ 0 & e^{-t}\end{pmatrix},故選\bbox[red, 2pt]{(C)}$$
解:
只有(B)的rank是2,其它都是1,故選\(\bbox[red, 2pt]{(B)}\)
解:$$令\cases{M(x,y)=x+y\\ N(x,y)=x\ln(x)}\\(A)\times: \cases{{\partial \over \partial y}xM = {\partial \over \partial y}(x^2+xy) = x\\{\partial \over \partial x}xN ={\partial \over \partial x}(x^2\ln(x))= 2x\ln(x)+x } \Rightarrow {\partial \over \partial y}xM \ne {\partial \over \partial x}xN \\(B) \times: \cases{{\partial \over \partial y}3M = {\partial \over \partial y}(3x +3y) = 3\\{\partial \over \partial x}3N ={\partial \over \partial x}(3x\ln(x))= 3\ln(x)+3 } \Rightarrow {\partial \over \partial y}3M \ne {\partial \over \partial x}3N \\(C)\bigcirc: \cases{{\partial \over \partial y}{1\over x}M = {\partial \over \partial y}(1 +{y\over x}) = {1\over x}\\{\partial \over \partial x}{1\over x}N ={\partial \over \partial x}\ln(x)= {1\over x} } \Rightarrow {\partial \over \partial y}{1\over x}M = {\partial \over \partial x}{1\over x}N \\(D)\times: \cases{{\partial \over \partial y}{1\over x^2}M = {\partial \over \partial y}({1\over x} +{y\over x^2}) = {1\over x^2}\\{\partial \over \partial x}{1\over x^2}N ={\partial \over \partial x}{\ln(x) \over x}= -{\ln(x)\over x^2}+{1\over x^2} } \Rightarrow {\partial \over \partial y}{1\over x^2}M \ne {\partial \over \partial x}{1\over x^2}N\\ ,故選\bbox[red,2pt]{(C)}$$
解:$$y''-6y'+9y = t^2e^{3t} \Rightarrow L\{y''\}-6L\{y'\}+9L\{y\} =L\{t^2e^{3t}\}\\ \Rightarrow s^2Y(s)-sy(0)-y'(0)-6(sY(s)-y(0))+ 9Y(s)= \frac{2!}{(s-3)^{3}} \\ \Rightarrow s^2Y(s)-2s-6-6sY(s)+12+9Y(s)= \frac{2}{(s-3)^{3}} \\ \Rightarrow Y(s)= {2\over (s-3)^5}+{2 \over s-3 } ={2(s-3)^4+2\over (s-3)^5} ={2(s-c)^d+2 \over (s-a)^b} \Rightarrow \cases{a=3\\ b=5\\ c=3 \\ d=4} \\ \Rightarrow \cases{a+b+c+d =15 \\a+b+c-d= 7 \\a-b-c+d =-1 \\ -a+b-c+d =3 \ne -3},故選\bbox[red,2pt]{(D)}$$
解:$$f(x)=x^3 \Rightarrow f(x)為奇函數\Rightarrow a_0=0,a_n=0,故選\bbox[red,2pt]{(A)}$$
解:$$y=c_1e^x +c_2e^{-2x}+c_3xe^{-2x} \Rightarrow 1, -2,-2為\lambda^2 +a\lambda^2 +b\lambda+c=0之三根為\\ \Rightarrow \cases{a=-(1-2-2) =3\\ b=1\cdot(-2)+ (-2)\cdot (-2)+ (-2)\cdot 1=0\\ c=-1\cdot (-2)\cdot (-2)=-4} \Rightarrow a+b+c=-1,故選\bbox[red,2pt]{(D)}$$
解:$$f(t)=\cos t +\int_0^t e^{-\tau}f(t-\tau)\;d\tau \Rightarrow L\{f(t)\} = L\{\cos t\} +L\{\int_0^t e^{-\tau}f(t-\tau)\;d\tau\} \\ \Rightarrow F(s)={s\over s^2+1} +{F(s)\over s+1} \Rightarrow F(s)={s+1\over s^2+1} ={s\over s^2+1} +{1\over s^2+1} \\ \Rightarrow L^{-1}\{F(s)\}= L^{-1}\{{s\over s^2+1}\}+L^{-1}\{{1\over s^2+1}\} \Rightarrow f(t) =\cos t+\sin t,故選\bbox[red,2pt]{(D)}$$
解:$$f為機率密度函數\Rightarrow \int_{-\infty}^\infty f(x)\;dx=1 \Rightarrow \int_{0}^1 kx^2\;dx =1 \Rightarrow \left. \left[ {1\over 3}kx^3 \right] \right|_{0}^1=1 \Rightarrow {1\over 3}k=1 \Rightarrow k=3\\ \Rightarrow \cases{EX = \int_0^1 xf(x)\;dx =\int_0^1 3x^3\;dx = {3\over 4}\\ EX^2 =\int_0^1 x^2f(x)\;dx = \int_0^13x^4\;dx = {3\over 5}} \Rightarrow \sigma^2 = EX^2-(EX)^2 = {3\over 5} -{9\over 16}= {3\over 80}\\,故選\bbox[red,2pt]{(D)}$$
解:$$ \iint fdxdy=1 \Rightarrow \int_0^1 \int_0^1 kxy \;dxdy =1 \Rightarrow \int_0^1 {1\over 2}ky\;dy =1 \Rightarrow {1\over 4}k = 1 \Rightarrow k=4;\\ 因此P(X>0.25,Y>0.5) = \int_{0.25}^1 \int_{0.5}^1 4xy\;dydx =\int_{0.25}^1 {3\over 2}x\;dx = {45 \over 64},故選\bbox[red, 2pt]{(C)}$$
解:$$z_0=\pi不在圓周|z|=3內,而z_0=\pi/2則在圓周|z|=3內,\\因此\oint_C\left({\cosh z\over (z-\pi)^3} -{\sin^2 z\over (2z-\pi)^3} \right)dz =\oint_C\left( -{\sin^2 z\over (2z-\pi)^3} \right)dz =\oint_C\left( -{\sin^2 z\over 8(z-\pi/2)^3} \right)dz \\=\oint_C {f(z)\over (z-\pi/2)^3} dz , 其中f(z)=-{1\over 8}\sin^2 z \Rightarrow f'(z)=-{1\over 4}\sin z\cos z =-{1\over 8} \sin (2z) \\\Rightarrow f''(z)= -{1\over 4}\cos (2z) \Rightarrow f''(\pi/2)=-{1\over 4}\cos \pi={1\over 4} \\\Rightarrow \oint_C {f(z)\over (z-\pi/2)^3} dz =(2\pi i)\times {1\over 2!}\times f''(\pi/2) = {\pi i\over 4},故選\bbox[red, 2pt]{(A)}$$
解:$${z\over (z+1)(z^2+1)}={z\over (z+1)(z+i)(z-i)} ={f(z)\over z-i} ={g(z)\over z+i},其中\cases{f(z)={z\over (z+1)(z+i) }\\ g(z)={z\over (z+1) (z-i)}}\\ -1不再橢圓內,而\pm i在橢圓內,因此\oint_C{z\over (z+1)(z^2+1)}\;dz = 2\pi i(f(i)+g(-i)) \\=2\pi i({i\over (1+i)(2i)} +{-i\over (1-i)(-2i)}) =2\pi i({1-i\over 4} +{1+i\over 4}) =\pi i,故選\bbox[red, 2pt]{(C)}$$
解:$$z_0={1+i\over \sqrt 2} =\cos {\pi \over 4}+i\sin {\pi \over 4} =e^{i{\pi\over 4}} \Rightarrow \cases{z_0^2 =i\\z_0^4=-1\\ z_0^8=1} \\ \Rightarrow f(z_0) =z_0^{24}- 3z_0^{20}+4z_0^{12}-5z_0^6 =(z_0^{8})^3- 3(z_0^{4})^5+4(z_0^{4})^3-5z_0^4\cdot z_0^2\\ = 1+3-4+5i=5i,故選\bbox[red, 2pt]{(A)}$$
解:$$\oint_\Gamma {\cos (z)\over z}\;dz = \oint_\Gamma {f(z)\over z}\;dz = 2\pi i\times f(0)=2\pi i\times 1 =2\pi i,故選\bbox[red, 2pt]{(D)}$$
解:封閉路徑之線積分為0,故選\(\bbox[red, 2pt]{(C)}\)
解:$$\cases{p_X(1)=0+1/4=1/4\\ p_X(0)=1/4+1/4=1/2\\ p_X(-1)=1/4+0 =1/4} \Rightarrow E(X)=1\cdot{1\over 4} +0\cdot {1\over 2} +(-1)\cdot {1\over 4}=0\\ \cases{p_Y(1)=0+1/4 +1/4=1/2\\ P_Y(-1)=1/4+1/4+0 =1/2} \Rightarrow E(Y)=1\cdot {1\over 2}-1\cdot {1\over 2}=0\\ E(XY) = \sum xyp(x,y) \\= 1\cdot 1\cdot p(1,1)+ 1\cdot (-1)\cdot p(1,-1)+ (-1)\cdot 1\cdot p(-1,1)+ (-1)\cdot (-1)\cdot p(-1,-1) \\=0 -1/4-1/4+0 = -1/2\\ 因此 COV(X,Y)= E(XY)-EXEY =-1/2-0=-1/2,故選\bbox[red, 2pt]{(B)}$$
=====================================================
申請論未公布答案,解題僅供參考






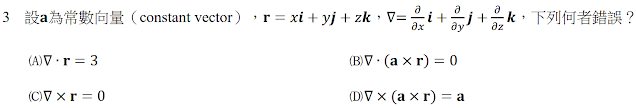

















作者已經移除這則留言。
回覆刪除有過程可以分享嗎? 謝謝!
刪除不好意思,請問第二題的第二小題是否寫錯了?
回覆刪除