110年警專40期數學科(甲組)詳解

臺灣警察專科學校110學年度專科警員班

第40期正期學生組新生入學考試甲組數學試題

壹、單選題

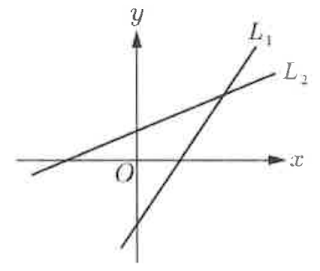
解答：$$y=\cos x 的週期為2\pi，在一個週期內，y={1\over 4}有兩個解；\\在二個週期[-2\pi,2\pi]有4個解，也就是4個交點，故選\bbox[red, 2pt]{(D)}$$

解答：$$\cases{L_1:ax-y+b=0\\ L_2:cx-y+d=0} \Rightarrow \cases{L_1斜率=a\\ L_2斜率=c}；由圖形知 \cases{a\gt c，且a,c \gt 0\\ b \lt 0 \\ d \gt 0} \Rightarrow d\gt b，故選\bbox[red, 2pt]{(D)}$$

解答：$$-3 \le x\le 5 \Rightarrow -4 \le x-1 \le 4 \Rightarrow |x-1| \le 4 \Rightarrow |-x+1|\le 4\equiv |ax+1| \le b \\\Rightarrow \cases{a=-1 \\ b=4}，故選\bbox[red, 2pt]{(C)}$$

解答：$$\cases{7x+3y=10 \\5x-3y=2} \Rightarrow \cases{x=1\\ y=1} ，即(1,1,z),z \in R 為一平行z軸的直線，故選\bbox[red, 2pt]{(D)}$$

解答：$$取法有4男1女(C^5_4C^5_1)、3男2女(C^5_3C^5_2)、2男3女(C^5_2C^5_3)、1男4女(C^5_1C^5_4)，\\共有5\times 5+10\times 10+ 10\times 10 + 5\times 5=250種取法，故選\bbox[red, 2pt]{(A)}$$

解答：$$f(x) = x^5-4x^4-72x^3- 56x^2+15x+8 \\ \Rightarrow f(11)= 11^5-4\cdot 11^4-72\cdot 11^3- 56\cdot 11^2+15\cdot 11+8 \\ =(11-4)11^4-72\cdot 11^3- 56\cdot 11^2+15\cdot 11+8 \\=7\cdot 11^4-72\cdot 11^3- 56\cdot 11^2+15\cdot 11+8 \\ =5\cdot 11^3- 56\cdot 11^2+15\cdot 11+8 = - 11^2+15\cdot 11+8 =4\cdot 11+8\\ =52，故選\bbox[red, 2pt]{(B)}$$

解答：$$y=ax^2 +bx+{3\over a}在x=-2有最大值-1 \Rightarrow \cases{y(-2)=-1\\ y'(-2)=0} \Rightarrow \cases{4a-2b+{3\over a}=-1 \cdots(1)\\ -4a+b=0 \cdots (2)}\\ 由(2) \Rightarrow b=4a 代入(1) \Rightarrow 4a-8a+{3\over a}=-1 \Rightarrow 4a^2-a-3=0 \Rightarrow (4a+3)(a-1)=0\\ \Rightarrow a=-{3\over 4} (a=1不合，違反y有最大值) \Rightarrow b=4a =-3，故選\bbox[red, 2pt]{(D)}$$

解答：$$\cases{a=2^{-1/2} = {1\over \sqrt 2} \\ b=3^{-1/3} ={1\over \sqrt[3] 3} \\ c=4^{-1/4}=2^{-1/2} = a} \Rightarrow \cases{a^6= {1\over 8} \\ b^6={1\over 9}} \Rightarrow a =c\gt b，故選\bbox[red, 2pt]{(C)}$$

解答：$$\log x+\log y=2 \Rightarrow \log (xy)=2 \Rightarrow xy=10^2=100;\\ 令k={4\over x}+{1\over y}= {x+4y\over xy} ={x+4y\over 100}，其中 4x+y \ge 2\sqrt{4xy}=40\\ \Rightarrow k \ge {40\over 100}={2\over 5} \Rightarrow {4\over x}+{1\over y }最小值為{2\over 5}，故選\bbox[red, 2pt]{(D)}$$

解答：$$2\log (7-x)= \log 2+\log(x-3) \Rightarrow \log (7-x)^2 = \log 2(x-3) \Rightarrow (7-x)^2=2(x-3)\\ \Rightarrow x^2-14x+49= 2x-6 \Rightarrow x^2-16x+55=0 \Rightarrow (x-5)(x-11)=0 \\\Rightarrow x=5 (x=11不合，違反 7-x \gt 0)，故選\bbox[red, 2pt]{(B)}$$

解答：$$3-i為一根，則3+i也為一根，因此(x-(3-i))(x-(3+i))= x^2-6x+10為f(x)的因式\\ 利用長除法，可得f(x)=(x^2-6x+10)(x+a+6)+(6(a+6)-6)x+ 10-10(a+6)\\ 餘式為0 \Rightarrow a=-5 \Rightarrow f(x)=(x^2-6x+10)(x+1) \Rightarrow f(x)=0的另一根為-1，故選\bbox[red, 2pt]{(A)}$$

解答：$$\cases{a_4=42 \\ a_{10}=27} \Rightarrow \cases{a_1+3d=42 \\ a_1+9d=27} \Rightarrow \cases{a_1=99/2 \\d=-5/2} \Rightarrow S_n = {n(2a_1+(n-1)d)}\div 2 \\ ={1\over 2}dn^2 +(a_1-{d\over 2})n \Rightarrow {d\over dn}S_n=0 \Rightarrow dn+(a_1-{d\over 2}) =0 \Rightarrow n=({d\over 2}-a_1)/d \\ ={1\over 2}+{99\over 5} =20.3 \approx 20，故選\bbox[red, 2pt]{(C)}$$

解答：$$f(x)= (ax-{1\over x^3})^8 = \sum_{k=0}^8 C^8_k(ax)^k\cdot (-{1\over x^3})^{8-k}  = \sum_{k=0}^8 C^8_k (-1)^{8-k}a^k   x^{4k-24} \\ 當k=6時，常數項=C^8_6(-1)^{2}a^6 =1792 \Rightarrow a^6= 1792\div 28= 64 \Rightarrow a=2，故選\bbox[red, 2pt]{(A)}$$

解答：$$迴歸直線方程式: y-\mu_y = r{\sigma_y\over \sigma_x}(x-\mu_x)經過(63,68)  \Rightarrow 68-65= {2\over 3}\cdot {\sigma_y \over 2} \cdot (63-60)\\ \Rightarrow \sigma_y =3，故選\bbox[red, 2pt]{(C)}$$

解答：$$\sin \theta- \cos \theta=-{1\over 5} \Rightarrow (\sin \theta- \cos \theta)^2 = 1-2\sin\theta \cos \theta={1\over 25} \Rightarrow 2\sin\theta \cos \theta ={24\over 25} \\ 又(\sin \theta +\cos \theta)^2 = 1+2 \sin \theta \cos \theta =1 + {24\over 25} ={49\over 25} \Rightarrow \sin \theta +\cos \theta={7\over 5} \\ 由\cases{\sin \theta- \cos \theta=-{1\over 5} \\ \sin \theta +\cos \theta={7\over 5}} \Rightarrow \cases{\sin \theta =3/5\\ \cos\theta =4/5} \Rightarrow \tan \theta =3/4，故選\bbox[red, 2pt]{(A)}$$

解答：

$$\angle C=90^\circ \Rightarrow \overline{BD}為直徑 \Rightarrow \angle A=90^\circ \Rightarrow \overline{BD}^2= \overline{AB}^2 +\overline{AD}^2 = 12^2+16^2 =20^2 \\ \Rightarrow 直徑=2r=\overline{BD}=20 \Rightarrow 半徑r=10;\\圓周角\angle ADC=60^\circ \Rightarrow 圓心角\angle AOC=120^\circ ；\\再利用餘弦定理: \cos \angle AOC={\overline{OA}^2 +\overline{OC}^2 -\overline{AC}^2 \over 2\cdot \overline{OA} \cdot \overline{OC}}  \Rightarrow -{1\over 2} ={10^2 +10^2 -\overline{AC}^2 \over 2\cdot 10\cdot 10} \\ \Rightarrow \overline{AC}^2 =300 \Rightarrow \overline{AC}=10\sqrt 3，故選\bbox[red, 2pt]{(B)}$$

解答：$$A=\begin{bmatrix} a & c\\ b & d\end{bmatrix}，則\cases{A\begin{bmatrix} 7\\ 3\end{bmatrix} =\begin{bmatrix} 2\\ 1\end{bmatrix} \\A\begin{bmatrix} 9\\ 4\end{bmatrix} =\begin{bmatrix} 1\\ 5\end{bmatrix} } \Rightarrow \cases{\begin{bmatrix} a & c\\ b & d\end{bmatrix}\begin{bmatrix} 7\\ 3\end{bmatrix} =\begin{bmatrix} 2\\ 1\end{bmatrix} \\\begin{bmatrix} a & c\\ b & d\end{bmatrix}\begin{bmatrix} 9\\ 4\end{bmatrix} =\begin{bmatrix} 1\\ 5\end{bmatrix} }  \\ \Rightarrow \cases{\cases{7a+3c=2 \\9a+4c=1} \\\cases{7b+3d=1 \\ 9b+4d=5}} \Rightarrow \cases{a=5\\ b=-11\\ c=-11\\ d=26}，故選\bbox[red, 2pt]{(B)}$$

解答：$$\cases{圓心O(-1,2) \\ P(3,5)} \Rightarrow \overrightarrow{OP} =(4,3) \Rightarrow 過P且法向量為(4,3)的直線L方程式:4(x-3)+3(y-5)=0\\ \Rightarrow (0,9)在L上，故選\bbox[red, 2pt]{(A)}$$

解答：$$(\sin \theta +\cos \theta)^2 = 1+2\sin \theta \cos \theta = 1+\sin 2\theta \Rightarrow \sin \theta +\cos \theta = \sqrt{1+\sin 2\theta}\\ 因此\cases{(A)\sin 12^\circ +\cos 12^\circ =\sqrt{1+\sin 24^\circ} \\(B) \sin 32^\circ +\cos 32^\circ =\sqrt{1+\sin 64^\circ} \\(C) \sin 52^\circ +\cos 52^\circ =\sqrt{1+\sin 104^\circ}  =\sqrt{1+\sin 86^\circ}\\(D) \sin 72^\circ +\cos 72^\circ =\sqrt{1+\sin 144^\circ} =\sqrt{1+\sin 36^\circ}} \Rightarrow (C)最大，故選\bbox[red, 2pt]{(C)}$$

解答：$${英文及格且數學不及格 \over 英文及格人數} ={2/5-1/3\over 1-3/8} ={1/15\over 5/8} ={8 \over 75}，故選\bbox[red, 2pt]{(B)}$$

解答：$$\vec a+\vec b+ \vec c=\vec 0 \Rightarrow \vec a+\vec b=-\vec c \Rightarrow |\vec a+\vec b|= |-\vec c| = 5 \Rightarrow |\vec a+\vec b|^2=25 \\又|\vec a+\vec b|^2 = (\vec a+\vec b) \cdot (\vec a+\vec b)= |\vec a|^2+ 2\vec a\cdot \vec b+|\vec b|^2= 4+ 2\vec a\cdot \vec b+9=25 \\ \Rightarrow \vec a\cdot \vec b=\vec a\cdot \vec b=6 \cdots(1)\\ |\vec a+2\vec b+3\vec c|^2 =|\vec a+2\vec b+3(-\vec a-\vec b)|^2 = |-2\vec a-\vec b |^2 =|2\vec a+\vec b |^2 =(2\vec a+\vec b) \cdot (2\vec a+\vec b) \\ =4|\vec a|^2 +|\vec b|^2 +4\vec a\cdot \vec b=16+9+ 24=49(將(1)代入) \Rightarrow |\vec a+2\vec b+3\vec c|=\sqrt{49}=7，故選\bbox[red, 2pt]{(C)}$$

解答：$$(x^2+y^2)(x^2-y^2)=0 \Rightarrow x^2-y^2=0 \Rightarrow (x+y)(x-y)=0 \Rightarrow x+y=0或x-y=0\\ 也就是兩條直線，故選\bbox[red, 2pt]{(B)}$$

解答：$$|\vec a||\vec b|\sin \theta =|\vec a\times \vec b|  \Rightarrow 2\cdot 7\cdot \sin \theta = |(3,6,-2)| \Rightarrow 14\sin \theta = \sqrt{3^2+6^2+(-2)^2} =7\\ \Rightarrow \sin \theta ={7\over 14} ={1\over 2}，故選\bbox[red, 2pt]{(A)}$$

解答：$$\angle ADB=90^\circ \Rightarrow \overline{BD}^2 =\overline{AB}^2-\overline{AD}^2=24^2-15^2 = 351；\\ \angle CBD=90^\circ \Rightarrow \overline{BC}^2 =\overline{CD}^2-\overline{BD}^2= 20^2-351=49 \Rightarrow \overline{BC}=7\\ \Rightarrow \sin \theta ={\overline{BC}\over \overline{CD}} ={7\over 20}，故選\bbox[red, 2pt]{(A)}$$

解答：$${x^2\over 169} +{y^2 \over 144} \Rightarrow \cases{a=13\\ b=12} \Rightarrow \cases{M=a^2=169\\ m=b^2=144}，故選\bbox[red, 2pt]{(A)}$$

解答：$$z={(3-4i)(2-5i) \over (5+2i)(12-5i)} \Rightarrow |z|= {|3-4i||2-5i |\over |5+2i||12-5i|} ={5\cdot \sqrt{29} \over \sqrt {29} \cdot 13} ={5\over 13}，故選\bbox[red, 2pt]{(B)}$$

解答：$$(2,0,0),(0,-6,0),(0,0,4)在E上\Rightarrow E:{x\over 2}-{y\over 6}+{z\over 4}=1\\ \Rightarrow 原點至E的距離={1\over \sqrt{{1\over 4}+ {1\over 26}+{1\over 16}}} ={1\over {7\over 12}} ={12\over 7}，故選\bbox[red, 2pt]{(D)}$$

解答：$$(A) \lim_{n\to \infty} {3n^2+5 \over 2n+7} = \infty \\(B) \lim_{n\to \infty}{2^n+5^n \over 4^n+ 3^n} = \infty\\ (C) \lim_{n\to \infty}\sqrt{n^2+n+1}-n = \lim_{n\to \infty}{ n^2+n+1 -n^2 \over \sqrt{n^2+n+1}+n} = \lim_{n\to \infty}{ n+1   \over \sqrt{n^2+n+1}+n} \\\qquad =\lim_{n\to \infty}{ 1+1/n   \over \sqrt{1+1/n+1/n^2}+1}=1/2\\ (D)\lim_{n\to \infty} \cos (n\pi)= \pm 1\\，故選\bbox[red, 2pt]{(C)}$$

解答：$$\cases{x+ 2y+3z=6\cdots(1)\\ 2x-y+z=2 \cdots(2)\\ 3x+y +4z=k \cdots(3)} \Rightarrow \triangle =\begin{vmatrix} 1 & 2& 3\\ 2 & -1 & 1\\ 3 & 1 & 4\end{vmatrix} =0，\Rightarrow 有無限多組解\\ \cases{2\times(2)+(1) \Rightarrow 5x+5z=10\\ (2)+(3) \Rightarrow 5x+5z=k+2}有無限多解\Rightarrow k+2=10 \Rightarrow k=8，故選\bbox[red, 2pt]{(D)}$$

解答：$$x={\pi\over 2}，所有選項皆不正確，本題\bbox[blue, 2pt]{送分}$$

貳、多重選題題

解答：$$(A)\times: \begin{bmatrix} 1 & 4\\ 2 & 0\end{bmatrix}\begin{bmatrix} a\\   0\end{bmatrix} =\begin{bmatrix} a\\   2a \end{bmatrix} \\(B)\bigcirc:\begin{bmatrix} 0 & 1\\ -1 & 0\end{bmatrix}\begin{bmatrix} a\\  0\end{bmatrix} =\begin{bmatrix} 0\\   -a \end{bmatrix} \\(C)\times:\begin{bmatrix} -1 & 2\\ 3 & -6\end{bmatrix}\begin{bmatrix} a\\   0\end{bmatrix} =\begin{bmatrix} -a\\   3a \end{bmatrix} \\(D)\bigcirc: \begin{bmatrix} 0 & 3\\ 2 & 1 \end{bmatrix} \begin{bmatrix} a\\   0\end{bmatrix} =\begin{bmatrix} 0\\   2a \end{bmatrix} \\(E)\times:\begin{bmatrix} 2 & 1\\ -1 & 0 \end{bmatrix}\begin{bmatrix} a\\   0\end{bmatrix} =\begin{bmatrix} 2a\\   -a \end{bmatrix}\\，故選\bbox[red, 2pt]{(BD)}$$

解答：$$(A)\times: \cases{X\sim B(10,0.5)\\ Y\sim B(10,0.8)} \Rightarrow \cases{E(X)=np=5\\ E(Y)= np=8} \Rightarrow E(Y) \gt E(X)\\ (B)\bigcirc: \cases{Var(X)=np(1-p)=10 \cdot 0.5\cdot 0.5=2.5\\ Var(Y)= 10\cdot 0.8\cdot 0.2=1.6} \Rightarrow Var(X) \gt Var(Y) \\(C)\bigcirc: P(X\le 5) = \sum_{k=0}^5C^{10}_k0.5^k0.5^{10-k} =0.5^{10}(C^{10}_0+ C^{10}_1+ C^{10}_2+ C^{10}_3+ C^{10}_4+ C^{10}_5)\\ \qquad ={638 \over 1024} \ge 0.5 \\(D)\times: p=0.8，圖形為左偏，也就是P(Y\le 5) \lt {1\over 2} \\(E)\bigcirc: \cases{X\sim B(10,0.5)\\ Y\sim B(10,0.8)} \Rightarrow \cases{X圖形對稱\\ Y圖形左偏} \quad\Rightarrow P(Y\gt 5) \ge P(X\gt 5)\\，故選\bbox[red, 2pt]{(BCE)}$$

解答：$$(B)\times: 有無限多\\(C)\times: 有無限多\\(D)\times:有無限多\\，故選\bbox[red, 2pt]{(AE)}$$

解答：$$(B)\times:  由於2^x \gt x \Rightarrow -x \gt -2^x，所以無交點\\ (D)\times:2^x \gt x \Rightarrow 2^{|x|} \gt |x| \ge -x，所以無交點，故選\bbox[red, 2pt]{(ACE)}$$

解答：$$\cases{P(x,y)\\ F_1(3,2)\\ F_2(-3,2)} \Rightarrow \Gamma:|\overline{PF_1}-\overline{PF_2}|= k；由於\overline{F_1F_2}= 6，因此0\lt k\lt 6才是雙曲線，故選\bbox[red, 2pt]{(AB)}$$

解答：$$(A)\times: \sum_{n=1}^\infty 1= 1+1 +\cdots =\infty \\(B)\times: 調和數列發散，即\sum_{n=1}^\infty{1\over n}=\infty \\(C) \bigcirc: \sum_{n=1}^\infty{1\over 2^n} ={1/2\over 1-1/2} =1\\(D) \bigcirc: \sum_{n=1}^\infty{1\over n(n+1)} =\sum_{n=1}^\infty \left( {1\over n }-{1\over n+1}\right) = 1-{1\over 2}+{1\over 2}-{1\over 3}+\cdots=1 \\(E) \times: \sum_{n=1}^\infty{1\over n(n+2)} =\sum_{n=1}^\infty {1\over 2}\left( {1\over n }-{1\over n+2}\right) ={1\over 2}(1-{1\over 3} +{1\over 2}-{1\over 4}+ {1\over 3}-{1\over 5} +{1\over 4}-{1\over 6}+\cdots )\\ \qquad ={1\over 2}(1+{1\over  2}) ={3\over 4}，故選\bbox[red, 2pt]{(CD)}$$

解答：$$\tan \theta =-4 \Rightarrow P(x,5)在y=-4x上\Rightarrow P(-{5\over 4},5) \Rightarrow \cases{\sin \theta =4/\sqrt{17} \\ \cos \theta =-1/\sqrt{17}} \\ \Rightarrow \cases{\sin(-\theta)=-\sin\theta= -4/\sqrt{17}\\ \sin(90^\circ +\theta)= \cos\theta=-1/\sqrt{17} =-17/\sqrt{17}\\ \cos(180^\circ-\theta) = -\cos \theta = 1/\sqrt{17}= 17/\sqrt{17}}，故選\bbox[red, 2pt]{(CDE)}$$

解答：$$(A)\bigcirc: 恰有一組解\Rightarrow \begin{vmatrix} k& 2\\ 2 & k\end{vmatrix} \ne 0 \Rightarrow (k+2)(k-2)\ne 0\Rightarrow k\ne 2,-2\\ (B)\times: k=2 \Rightarrow \cases{2x+ 2y=5 \\ 2x+2y =5} \Rightarrow 兩式相同，有無限多解\\ (C)\bigcirc: k=-2 \Rightarrow \cases{-2x+2y = -3\\ 2x-2y=9} \Rightarrow \cases{2x-2y = 3\\ 2x-2y=9} \Rightarrow 無解 \\(D)\times: 兩直線\cases{2x-2y = 3\\ 2x-2y=9} 距離={6\over \sqrt{2^2+2^2}} ={3\over \sqrt 2}\ne 2 \\(E)\bigcirc: 2x+2y=5的斜率為-1\\，故選\bbox[red, 2pt]{(ACE)}$$

解答：$$\cases{a_n= C^4_n{1\over 2^4}  \\b_n= C^8_n {1\over 2^8}} \\ (A)\times: a_2=C^4_2 {1\over 2^4}= {3\over 8}\\ (B) \times:  b_4=C^8_4{1\over 2^8} ={35\over 128} \ne a_2\\ (C)\bigcirc: C^8_2=C^8_6 \Rightarrow b_2=b_6\\ (D)\bigcirc: \cases{a_3 =C^4_3{1\over 2^4} = 1/4=8/32 \\ b_3=C^8_3{1\over 2^8} =56/256 =7/32} \Rightarrow a_3\gt b_3 \\(E)\times: \max\{C^8_n,n\in[0,8]\} =C^8_4 \Rightarrow  \max\{b_n,n\in[0,8]\}=b_4\ne b_5\\，故選\bbox[red, 2pt]{(CD)}$$

解答：$$(A)\times: \omega = e^{i2\pi/7} \Rightarrow \omega^{110} =e^{i220\pi/7} =e^{i(30+10\pi/7)} =e^{i( 10\pi/7)} =\omega^5\ne 1 \\(B)\bigcirc: \omega = e^{i2\pi/7} \Rightarrow\omega^7=1 \Rightarrow \omega^7-1=0 \Rightarrow (\omega-1)(\omega^6+ \omega^5+\cdots +\omega+1)=0\\ \qquad 令\omega'=1+\omega +\cdots +\omega^6=0 \Rightarrow 1+\omega+\cdots +\omega^{21}= \omega'+ \omega^7\omega' +\omega^{14}\omega'+\omega^{21} =\omega^{21}=1 \\(C)\bigcirc: \omega^7=1 \Rightarrow \omega^6={1\over \omega}= \bar \omega \\(D)\bigcirc: f(x)=1+x^2+\cdots +x^6=0的六根為\omega,\omega^2,\dots, \omega^6 \Rightarrow f(x)=(x-\omega)(x-\omega^2)\dots (x-\omega^6)\\ \qquad \quad \Rightarrow f(1)= 1+1+\cdots +1=7 =(1-\omega)(1-\omega^2) \cdots (1-\omega^5)(1-\omega^6) \\ \qquad \quad \Rightarrow (1-\omega)(1-\omega^2) (1-\omega^3)(1-\omega^4)(1-\omega^5)(1-\omega^6)=7 \\\times: (E)由(D)知|(1-\omega)\cdots (1-\omega^6)|= |(1-\omega)(1-\omega^2)(1-\omega^3)(1-\overline{\omega^3}) (1-\overline{\omega^2})(1-\overline{\omega}) | \\ \qquad \quad =|(1-\omega)(1-\omega^2)(1-\omega^3)||(1-\overline{\omega^3}) (1-\overline{\omega^2})(1-\overline{\omega})| \\ \qquad \quad = |(1-\omega)(1-\omega^2)(1-\omega^3)|^2 =7\\\qquad \quad\Rightarrow |(1-\omega)(1-\omega^2)(1-\omega^3)|=|(1-\omega)||(1-\omega^2)||(1-\omega^3)| =\sqrt 7\\，故選\bbox[red, 2pt]{(BCD)}$$
 =========== END ==========

解題僅供參考，其它警專試題及詳解