國立臺北科大附屬桃園農工 110 學年度第一次教師甄試
解答:(1)$$令\cases{\log_c b= x\\ \log_c a=y} \Rightarrow {\log_c b\over \log_c a}={x\over y} \Rightarrow \log_c b-{x\over y}\log_c a=0 \Rightarrow \log_c{b\over a^{x/y}} =0 \Rightarrow b= a^{x/y} \\ \Rightarrow \log_a b= {x\over y} \Rightarrow \log_a b= {\log_c b\over \log_c a},\bbox[red, 2pt]{故得證}$$(2)$$y=f(x)= \log_a (x-2)+x^3-28=0 \Rightarrow \log_a (x-2)=28-x^3 \\其解個數相當於兩圖形\cases{y=g(x)=\log_a (x-2)\\ y=h(x)=28-x^3} 的交點數,其中x \in [3,a+2];\\而h'(x)=-3x^2 \lt 0,\forall x \in R,因此\cases{y=g(x)為遞增\\ y=h(x)為遞減}\\ 又\cases{f(3)=0+3^3-28=-1 \lt 0\\ f(a+2)=1+ (a+2)^3-28 \gt 0 (\because a\gt 3)},因此有一交點,也僅有\bbox[red, 2pt]{一個交點}。$$(3)$$\cases{a,b\in \mathbb{N}\\ a+b=12\\ a\ne 1\\ b\ne 1} \Rightarrow (a,b)=(2,10),(3,9),\dots,(10,2),11種可能\\ 再加上\log_b c= \log_a 4 \Rightarrow \begin{array}{}a & b & c \\\hline 2 & 10 & 100 \\ 3& 9 & 16 \\ 4 & 8 & 8 \\ 6 & 6 & 4 \\9 & 3 & 2\\\hline \end{array}\\ 即(a,b,c)= \bbox[red, 2pt]{(2,10,100), (3,9,16), (4,8,8), (6,6,4),(9,3,2)}$$
解答:
解答:
(1)$$C^{n+1}_3 = C^n_2+ C^n_3 =C^n_2 + (C^{n-1}_2 + C^{n-1}_3 ) = C^n_2 + C^{n-1}_2 + (C^{n-2}_2 +C^{n-2}_3 ) =\cdots \\ =C^n_2+ C^{n-1}_2 +C^{n-2}_2 +\cdots +C^2_2,\bbox[red, 2pt]{故得證}$$(2)$$C^n_2 ={n(n-1)\over 2} \Rightarrow n^2 = 2C^n_2 +n \Rightarrow \sum_{k=2}^n k^2 =\sum_{k=2}^n (2C^k_2 +k) =2 \sum_{k=2}^n C^k_2 +\sum_{k=2}^n k\\ = 2C^{n+1}_3 +{(n-1)(n+2) \over 2} = {(n-1)n(n+1)\over 3}+{(n-1)(n+2) \over 2} ={2n^3+3n^2+n-6 \over 6}\\ \Rightarrow \sum_{k=1}^n k^2 ={2n^3+3n^2+n-6 \over 6} +1 ={2n^3+3n^2+n \over 6} ={n(n+1)(2n+1) \over 6},\bbox[red, 2pt]{故得證}$$
解答:$$(1+x)^n= C^n_0+ C^n_1x +C^n_2x^2 +\cdots +C^n_nx^n\\ \Rightarrow \int_{-1}^0(1+x)^n\;dx = \int_{-1}^0C^n_0+ C^n_1x +C^n_2x^2 +\cdots +C^n_nx^n \;dx \\ \Rightarrow \left. \left[ {1\over n+1}(1+x)^{n+1} \right] \right|_{-1}^0 =\left. \left[ C^n_0x+{1\over 2} C^n_1x^2 + {1\over 3}C^n_2x^3 +\cdots + {1\over n+1}C^n_nx^{n+1} \right] \right|_{-1}^0 \\ \Rightarrow {1\over n+1} = 0-(-C^n_0+{1\over 2}C^n_1 -{1\over 3}C^n_2 +\cdots +{1\over n+1}(-1)^{n+1}C^n_n)\\ \Rightarrow C^n_0-{1\over 2}C^n_1 +{1\over 3}C^n_2+ \cdots + {1\over n+1}(-1)^nC^n_n ={1\over n+1},\bbox[red, 2pt]{故得證}$$
解答:
解答:$$(1+x)^n= C^n_0+ C^n_1x +C^n_2x^2 +\cdots +C^n_nx^n\\ \Rightarrow \int_{-1}^0(1+x)^n\;dx = \int_{-1}^0C^n_0+ C^n_1x +C^n_2x^2 +\cdots +C^n_nx^n \;dx \\ \Rightarrow \left. \left[ {1\over n+1}(1+x)^{n+1} \right] \right|_{-1}^0 =\left. \left[ C^n_0x+{1\over 2} C^n_1x^2 + {1\over 3}C^n_2x^3 +\cdots + {1\over n+1}C^n_nx^{n+1} \right] \right|_{-1}^0 \\ \Rightarrow {1\over n+1} = 0-(-C^n_0+{1\over 2}C^n_1 -{1\over 3}C^n_2 +\cdots +{1\over n+1}(-1)^{n+1}C^n_n)\\ \Rightarrow C^n_0-{1\over 2}C^n_1 +{1\over 3}C^n_2+ \cdots + {1\over n+1}(-1)^nC^n_n ={1\over n+1},\bbox[red, 2pt]{故得證}$$
解答:
(1)$$\left(({a\over \sqrt{2a+b}})^2 + ({b\over \sqrt{2b+c}})^2 +({c\over \sqrt{2c+a}})^2 \right) \left((\sqrt{2a+b})^2 +(\sqrt{2b+c})^2 +(\sqrt{2c+a})^2 \right)\\ \qquad\qquad \ge (a +b +c)^2\\ \Rightarrow \left({a^2 \over 2a+b} +{b^2 \over 2b+c} +{c^2 \over 2c+a} \right)(3(a+b+c)) \ge (a+b+c)^2 \\ \Rightarrow {a^2 \over 2a+b} +{b^2 \over 2b+c} +{c^2 \over 2c+a}\ge {a+b+c \over 3},\bbox[red, 2pt]{故得證}$$(2)$$算幾不等式:\cases{r_1^3+ r_2^3+r_3^3 \ge 3 \sqrt[3]{r_1^3 r_2^3r_3^3} =3r_1r_2r_3\cdots(1) \\ (r_1r_2)^3 +(r_2r_3)^3 +(r_3r_1)^3 \ge 3\sqrt[3]{ (r_1r_2)^3 (r_2r_3)^3 (r_3r_1)^3} =3r_1^2r_2^2r_3^2 \cdots(2)}\\ 令\cases{r_1=a_2/a_1 \\r_2= b_2/b_1\\ r_3=c_2/c_1},則 \cases{(a_1^3 +a_2^3)(b_1^3+b_2^3) (c_1^3+c_2^3) = a_1^3b_1^3c_1^3(1+r_1^3) (1+r_2^3)(1+r_3^3)\\ (a_1b_1c_1 +a_2b_2c_2)^3 = a_1^3b_1^3c_1^3(1+r_1r_2r_3)^3} \\ 由於 (1+r_1^3) (1+r_2^3)(1+r_3^3) \\= 1+ (r_1^3+ r_2^3+r_3^3) +((r_1r_2)^3 +(r_2r_3)^3 +(r_3r_1)^3) + r_1^3r_2^3r_3^3 \\ \ge 1+3r_1r_2r_3 + 3r_1^2r_2^2r_3^2 + r_1^3r_2^3r_3^3 =(1+r_1r_2r_3)^3 ( 將(1),(2)代入) \\ \Rightarrow 因此(1+r_1^3) (1+r_2^3)(1+r_3^3) \ge (1+r_1r_2r_3)^3\\ 也就是(a_1^3 +a_2^3)(b_1^3+b_2^3) (c_1^3+c_2^3) \ge (a_1b_1c_1 +a_2b_2c_2)^3,\bbox[red, 2pt]{故得證}$$
$$\cos \theta = {|\vec a|^2 +|\vec b|^2-|\vec c|^2 \over 2|\vec a||\vec b|} \Rightarrow |\vec c|^2= |\vec a|^2 +|\vec b|^2- 2|\vec a||\vec b| \cos \theta \cdots(1)\\ \vec c =\vec a-\vec b \Rightarrow |\vec c|^2 = (\vec a-\vec b)\cdot (\vec a-\vec b) =|\vec a|^2 +|\vec b|^2 -2\vec a\cdot \vec b \Rightarrow \vec a\cdot \vec b={|\vec a|^2 +|\vec b|^2-|\vec c|^2 \over 2} \cdots(2)\\ 將(1)代入(2) \Rightarrow \vec a\cdot \vec b=|\vec a||\vec b|\cos \theta,\bbox[red, 2pt]{故得證}$$
解答:$$\cases{{b\over a} +{a\over b}= {a^2+b^2 \over ab}=4\cos C \Rightarrow \cos C={a^2+b^2\over 4ab}\\ \cos C={a^2+b^2-c^2 \over 2ab}} \Rightarrow {a^2+b^2\over 4ab}={a^2+b^2-c^2 \over 2ab} \Rightarrow a^2+b^2=2c^2 \cdots(1)\\ \tan C(\cot A+\cot B) = {\sin C\over \cos C}\left({\cos A\over \sin A} +{\cos B\over \sin B} \right) ={\cos A\over \cos C}\cdot {\sin C\over \sin A} +{\cos B\over \cos C} \cdot {\sin C\over \sin B} \\ = \left({b^2+c^2-a^2\over 2bc} \cdot {2ab \over a^2+b^2-c^2} \right) \cdot {c\over a} + \left({a^2+c^2-b^2 \over 2ac} \cdot {2ab \over a^2+b^2-c^2}\right) \cdot {c\over b} \\ ={b^2+c^2-a^2\over a^2+b^2-c^2} +{a^2+c^2-b^2 \over a^2+b^2-c^2} ={ 2c^2\over a^2+b^2-c^2} ={2c^2 \over 2c^2-c^2} ((1)代入) =\bbox[red, 2pt]{2}$$
解答:
解答:$$\cases{{b\over a} +{a\over b}= {a^2+b^2 \over ab}=4\cos C \Rightarrow \cos C={a^2+b^2\over 4ab}\\ \cos C={a^2+b^2-c^2 \over 2ab}} \Rightarrow {a^2+b^2\over 4ab}={a^2+b^2-c^2 \over 2ab} \Rightarrow a^2+b^2=2c^2 \cdots(1)\\ \tan C(\cot A+\cot B) = {\sin C\over \cos C}\left({\cos A\over \sin A} +{\cos B\over \sin B} \right) ={\cos A\over \cos C}\cdot {\sin C\over \sin A} +{\cos B\over \cos C} \cdot {\sin C\over \sin B} \\ = \left({b^2+c^2-a^2\over 2bc} \cdot {2ab \over a^2+b^2-c^2} \right) \cdot {c\over a} + \left({a^2+c^2-b^2 \over 2ac} \cdot {2ab \over a^2+b^2-c^2}\right) \cdot {c\over b} \\ ={b^2+c^2-a^2\over a^2+b^2-c^2} +{a^2+c^2-b^2 \over a^2+b^2-c^2} ={ 2c^2\over a^2+b^2-c^2} ={2c^2 \over 2c^2-c^2} ((1)代入) =\bbox[red, 2pt]{2}$$
解答:
(1)$$AB=I \Rightarrow B(AB)=BI \Rightarrow BAB=B \Rightarrow BAB-B=0 \Rightarrow (BA-I)B=0\\ \Rightarrow BA=I (若B=0_n,則AB\ne I),\bbox[red, 2pt]{故得證}$$(2)$$\left[ \begin{array}{ccc|ccc}1 & 2 & 0 & 1 & 0 & 0\\ 2 & 3 & 0 & 0 & 1& 0\\ 0 & 1 & 2 & 0 & 0 & 1 \end{array}\right] \underrightarrow{-2r_1+r_2} \left[ \begin{array}{ccc|ccc}1 & 2 & 0 & 1 & 0 & 0\\ 0 & -1 & 0 & -2 & 1& 0\\ 0 & 1 & 2 & 0 & 0 & 1 \end{array}\right] \\ \underrightarrow{2r_2+r_1,r_2+r_3}\left[ \begin{array}{ccc|ccc}1 & 0 & 0 & -3 & 2 & 0\\ 0 & -1 & 0 & -2 & 1& 0\\ 0 & 0 & 2 & -2 & 1 & 1 \end{array}\right] \underrightarrow{-r_2 ,r_3/2 }\left[ \begin{array}{ccc|ccc}1 & 0 & 0 & -3 & 2 & 0\\ 0 & 1 & 0 & 2 & -1& 0\\ 0 & 0 & 1 & -1 & 1/2 & 1/2 \end{array}\right] \\ \Rightarrow A^{-1} = \bbox[red, 2pt]{\left[ \begin{array}{rrr}-3 & 2 & 0\\ 2 & -1& 0\\ -1 & 1/2 & 1/2 \end{array}\right]}$$
解答:$$題目的n應該是x \\ \\由於 \lim_{x\to 0^+} x\log (\sin x) =\lim_{x\to 0^+} {\log (\sin x) \over 1/x} =\lim_{x\to 0^+} {(\log (\sin x))' \over (1/x)'} = \lim_{x\to 0^+} {- x^2 \cos x\over \sin x} \\ =\lim_{x\to 0^+} (-x) \cdot \lim_{x\to 0^+} {x\over \tan x} =0 \cdot 1= 0 \\ 因此 \lim_{x\to 0^+} (\sin x)^x = \lim_{x\to 0^+} e^{x \log\sin x} =e^0= \bbox[red, 2pt]{1}$$
解答:$$f(x)= [\sin(x^2+1)]^x = e^{x\log \sin(x^2+1)} \\\Rightarrow f'(x) = (\log \sin(x^2+1) +{ 2x^2\cos(x^2+1)\over \sin(x^2+1)}) e^{x\log \sin(x^2+1)} \\ = \bbox[red, 2pt]{(\log \sin(x^2+1) + 2x^2\cot(x^2+1) ) [\sin(x^2+1)]^x}$$
解答:$$令u^2=1+x^3 \Rightarrow x=(u^2-1)^{1/3} \Rightarrow dx = {2\over 3}u(u^2-1)^{-2/3}du \\ \Rightarrow \int {x^5 \over \sqrt{1+x^3}}\;dx = \int {(u^2-1)^{5/3} \over u} \cdot {2\over 3}u(u^2-1)^{-2/3}du =\int {2\over 3}(u^2-1)\;du \\ ={2\over 3}({1\over 3}u^3-u)+C = \bbox[red, 2pt]{{2\over 9}(1+x^3)^{3/2}-{2\over 3}(1+x^2)^{1/2}+C,C為常數}$$
解答:$$\int {\cos x\over e^x}dx = e^{-x}\sin x+ \int e^{-x}\sin x\;dx\left(\because\cases{u=e^{-x}\\ dv = \cos xdx} \Rightarrow \cases{du=-e^{-x} dx\\ v=\sin x} \right) \\ =e^{-x}\sin x-e^{-x}\cos x-\int e^{-x} \cos x \;dx \left(\because\cases{u=e^{-x}\\ dv = \sin xdx} \Rightarrow \cases{du=-e^{-x} dx\\ v=-\cos x} \right) \\ \Rightarrow 2\int e^{-x}\cos x\;dx =e^{-x}\sin x-e^{-x}\cos x \Rightarrow \int e^{-x}\cos x\;dx = \bbox[red, 2pt]{{\sin x-\cos x\over 2e^x}+C,C為常數}$$
解答:$$題目的n應該是x \\ \\由於 \lim_{x\to 0^+} x\log (\sin x) =\lim_{x\to 0^+} {\log (\sin x) \over 1/x} =\lim_{x\to 0^+} {(\log (\sin x))' \over (1/x)'} = \lim_{x\to 0^+} {- x^2 \cos x\over \sin x} \\ =\lim_{x\to 0^+} (-x) \cdot \lim_{x\to 0^+} {x\over \tan x} =0 \cdot 1= 0 \\ 因此 \lim_{x\to 0^+} (\sin x)^x = \lim_{x\to 0^+} e^{x \log\sin x} =e^0= \bbox[red, 2pt]{1}$$
解答:$$f(x)= [\sin(x^2+1)]^x = e^{x\log \sin(x^2+1)} \\\Rightarrow f'(x) = (\log \sin(x^2+1) +{ 2x^2\cos(x^2+1)\over \sin(x^2+1)}) e^{x\log \sin(x^2+1)} \\ = \bbox[red, 2pt]{(\log \sin(x^2+1) + 2x^2\cot(x^2+1) ) [\sin(x^2+1)]^x}$$
解答:$$令u^2=1+x^3 \Rightarrow x=(u^2-1)^{1/3} \Rightarrow dx = {2\over 3}u(u^2-1)^{-2/3}du \\ \Rightarrow \int {x^5 \over \sqrt{1+x^3}}\;dx = \int {(u^2-1)^{5/3} \over u} \cdot {2\over 3}u(u^2-1)^{-2/3}du =\int {2\over 3}(u^2-1)\;du \\ ={2\over 3}({1\over 3}u^3-u)+C = \bbox[red, 2pt]{{2\over 9}(1+x^3)^{3/2}-{2\over 3}(1+x^2)^{1/2}+C,C為常數}$$
解答:$$\int {\cos x\over e^x}dx = e^{-x}\sin x+ \int e^{-x}\sin x\;dx\left(\because\cases{u=e^{-x}\\ dv = \cos xdx} \Rightarrow \cases{du=-e^{-x} dx\\ v=\sin x} \right) \\ =e^{-x}\sin x-e^{-x}\cos x-\int e^{-x} \cos x \;dx \left(\because\cases{u=e^{-x}\\ dv = \sin xdx} \Rightarrow \cases{du=-e^{-x} dx\\ v=-\cos x} \right) \\ \Rightarrow 2\int e^{-x}\cos x\;dx =e^{-x}\sin x-e^{-x}\cos x \Rightarrow \int e^{-x}\cos x\;dx = \bbox[red, 2pt]{{\sin x-\cos x\over 2e^x}+C,C為常數}$$
=========== END ===============
學校未公布答案,解題僅供參考,其它教甄試題及詳解




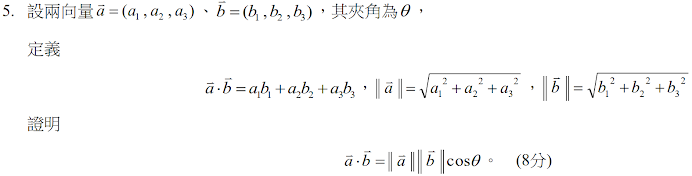






沒有留言:
張貼留言