106 年公務人員初等考試試題
等 別: 初等考試
類 科: 統計
科 目: 統計學大意
解答:$$P(X=1)=1/2 \Rightarrow P(X=k)=(1-1/2)\div 5=1/10,k=2-5;\\ 點數和小於等於4 \Rightarrow (X_1,X_2)=(1,1),(1,2),(1,3),(2,1),(2,2),(3,1) \\ \Rightarrow 機率為{1\over 2}\cdot {1\over 2}+ {1\over 2}\cdot {1\over 10}+{1\over 2}\cdot {1\over 10}+ {1\over 10}\cdot {1\over 2}+ {1\over 10}\cdot {1\over 10}+ {1\over 10}\cdot {1\over 2}\\ ={23\over 50} \Rightarrow 點數和 大於4的機率=1-{23\over 50} ={27\over 50} ,故選\bbox[red,2pt]{(A)}$$
解答:$${B工廠生產的不良品\over 不良品} ={0.7\times 0.03\over 0.3\times 0.08 +0.7\times 0.03} ={0.021\over 0.045} =0.4667,故選\bbox[red,2pt]{(C)}$$
解答:$$只有共變異數是計算兩個變數之間的關係,其他皆為一個變數的不同統計值,故選\bbox[red,2pt]{(B)}$$
解答:$$柴比雪夫不等式:P(|X-\mu|\lt k\sigma)\ge 1-{1\over k^2}\\欲求P(22 \lt X\lt 27)= P( |X-24.5|\lt {2.5\over 1.2}\cdot 1.2) \ge 1-{1\over (2.5/1.2)^2}={481\over 625} = 0.7696\\,故選\bbox[red,2pt]{(B)}$$
解答:$$心理學成績高於平均值,而微積分成績低於平均值,因此心理學比較好,故選\bbox[red,2pt]{(A)}$$
解答:$$B班成績較集中、A班成績較分散;且A班Q_2\lt B班Q_2,故選\bbox[red,2pt]{(D)}$$
解答:$$\cases{50\div 4=12.5 \Rightarrow Q_1為排名第13成績,即Q_1=62\\ 50\times 3\div 4=37.5 \Rightarrow Q_3為排名第38成績,即Q_3=79} \\ \Rightarrow IQR= Q_3-Q_1=79-62=17,故選\bbox[red,2pt]{(C)}$$
解答:$$(1-0.6)^3=0.064,故選\bbox[red,2pt]{(A)}$$
解答:$$常態分配\Rightarrow P(X\gt \mu)=0.5,故選\bbox[red,2pt]{(D)}$$
解答:$$簡單隨機可抽出任意結果,系統隨機需有平均分配的規律性;\\\cases{S1:數字集中在前4個\\S2、S5:數字間隔皆為25\\ S3、S4:無規律性 },故選\bbox[red,2pt]{(B)}$$
解答:$$P(X\lt 2)=0.005 \Rightarrow P(Z\lt {2-4\over \sigma})=0.005,查表可得P(Z\lt 2.575)=0.995\\ 因此{2-4\over \sigma}=-2.575 \Rightarrow \sigma = {2\over 2.575}=0.7767,故選\bbox[red,2pt]{(C)}$$
解答:$$\cases{E(X)=np = 30\times {80\over 200}=12\\ Var(X)=npq= 30\times {80\over 200}\times {120\over 200}=7.2} \Rightarrow E(X)\times Var(X)=12\times 7.2=86.4,無此選項\\由於{樣本數n\over 母體數N}={30\over 200}=0.15 \gt 5\%,因此需要校正因子{N-n\over N-1} ={200-30\over 200-1}=0.854\\ \Rightarrow 86.4\times 0.854=73.8,故選\bbox[red,2pt]{(A)}$$
解答:$$2z_{\alpha/2}\sqrt{p(1-p)\over n} =2\times 1.645\times \sqrt{{2\over 7}\cdot {5\over 7}\over 560}=0.0628,故選\bbox[red,2pt]{(C)}$$
解答:$$增加樣本數可以縮短信賴區間,其他選項皆加大區間長度,故選\bbox[red,2pt]{(B)}$$
解答:$$\cases{p_1=184/300\\ p_2=250/400} \Rightarrow 比例差異信賴區間=(p_1-p_2)\pm z_{\alpha/2}\sqrt{{p_1(1-p_1)\over n_1}+{p_2(1-p_2) \over n_2}} \\ =({184\over 300}-{250\over 400})\pm 1.96\times \sqrt{{{184\over 300}-{116\over 300}\over 300}+ {{250\over 400}-{150\over 400}\over 400}} =-0.012 \pm 1.96\times 0.037\\ =(-0.084,0.061),故選\bbox[red,2pt]{(A)}$$
解答:$$\overline{X}是\mu的不偏也是最大概似估計,而\hat \sigma^2 是\sigma^2的最大概似估計,故選\bbox[red,2pt]{(C)}$$
解答:$$\cases{Var(T_1)= Var({X_1+2X_2+ 3X_3\over 6})= \sigma^2({1\over 36} +{1\over 9} +{1\over 4} ) ={14\over 36}\sigma^2 \\ Var(T_2)= Var({X_1+X_2\over 2})=\sigma^2({1\over 4} +{1\over 4})={1\over 2}\sigma^2} \\ \Rightarrow Var(T_1)< Var(T_2) \Rightarrow T_1 較具有效性,故選\bbox[red,2pt]{(A)}$$
解答:$${\bar x-\mu\over \sigma/\sqrt n} \gt z_\alpha \Rightarrow {\bar x-5 \over 1.78/\sqrt{16}} \gt 1.645 \Rightarrow \bar x\gt 5.732,故選\bbox[red,2pt]{(C)}$$
解答:$$小樣本且兩母體變異數未知,但已知相等,自由度為n_1+n_2-2,故選\bbox[red,2pt]{(C)}$$
解答:$$95\%的信心被\text{ Reject} \Rightarrow p \lt 0.05 \Rightarrow p \lt 0.1 \Rightarrow 必定會在90\%信心下也被\text{ Reject},故選\bbox[red,2pt]{(B)}$$
解答:$$區間長度不超過0.12 \Rightarrow z_{\alpha/2}{\sigma \over \sqrt n} \lt {0.12\over 2} \Rightarrow 1.645 \cdot \sqrt{0.1\times 0.9 \over n} \lt 0.06 \Rightarrow {0.4935 \over \sqrt n}\lt 0.06\\ \Rightarrow n \gt 67.65,故選\bbox[red,2pt]{(C)}$$
解答:$$p\lt \alpha \Rightarrow 達顯著,故拒絕H_0,故選\bbox[red,2pt]{(B)}$$
解答:$$\cases{MSTR=50\\ SSTR=150} \Rightarrow 處理數量={SSTR\over MSTR}+1={150\over 50}+1=4,故選\bbox[red,2pt]{(B)}$$
解答:
$$\cases{df_B=5-1=4\\ df_W=65-1-4=60\\SSW=600-200=400 }\Rightarrow\cases{ MSB=200/df_B=50\\ MSW=SSW/df_W=20/3}\\ \Rightarrow F=MSB/MSW = 150/20= 7.5,故選\bbox[red,2pt]{(C)}$$
解答:$$A因子的自由度乘上B因子的自由度=(a-1)(b-1),故選\bbox[red,2pt]{(A)}$$
解答:$$SSE = MSE\times(n-2)=200\times 18= 3600 \Rightarrow SST= SSE+SSR = 3600+1600= 5200\\ \Rightarrow R^2 = 1-{SSE\over SST} =1-{36\over 52}=0.308,故選\bbox[red,2pt]{(C)}$$
解答:$$斜率={\sum(x-\bar x)(y-\bar y)\over \sum(x-\bar x)^2} ={2250\over 100\times (10-1)}=2.5;\\又迴歸直線經過(\bar x,\bar y),因此直線方程式為:y-\bar y=2.5(x-\bar x) \Rightarrow y-7.5=2.5(x-5)\\ \Rightarrow y=2.5x-5 \Rightarrow 截距為-5,故選\bbox[red,2pt]{(B)}$$
解答:$$判定係數R^2=0.81 \Rightarrow 相關係數 r=\pm \sqrt{0.81} =\pm 0.9\\ 又r={\text{cov}(x,y)\over S_x\cdot S_y} ={\text{cov}(x,y)\over \sqrt{1600}\cdot \sqrt{1225}} ={\text{cov}(x,y)\over 40\cdot 35} = 0.9 \Rightarrow \text{cov}(x,y)=1260,故選\bbox[red,2pt]{(A)}$$
解答:$$(\hat y(2)-8)^2 +(\hat y(1)-5)^2 +(\hat y(2)-7)^2 =(11-8)^2 +(6-5)^2 +(11-7)^2 = 9+1+16=26\\,故選\bbox[red,2pt]{(C)}$$
解答:$$迴歸直線斜率= 相關係數r\times {\sigma_y\over \sigma_x} \Rightarrow 4.568 = r\times {31.9043 \over 6.8336} \Rightarrow r= 0.9784 \\\Rightarrow R^2=r^2= 0.9573 ,故選\bbox[red,2pt]{(B)}$$
解答:$$連檢定\text{(Runs Test) 即是用來檢定樣本是否為隨機產生的};\\現在p=0.3685 \gt 5\% \Rightarrow 未達顯著,故選\bbox[red,2pt]{(A)}$$
解答:$$觀察值:\begin{array}{l|cc|r} & \lt 30 & \gt 30 & 小計\\\hline 職業婦女 & 42 & 38 & 80\\家庭主婦 & 38 & 62 & 100\\ \hdashline 小計 & 80 & 100 & 180\end{array} \\ \Rightarrow 期望值:\begin{array}{l|cc|r} & \lt 30 & \gt 30 & 小計\\\hline 職業婦女 & 80\cdot {4\over 9}=35.56 & 80\cdot {5\over 9}=44.44 & 80\\家庭主婦 & 100\cdot {4\over 9}=44.44 & 100\cdot {5\over 9}= 55.56& 100\\ \hdashline 小計 & 80 & 100 & 180\end{array}\\ \Rightarrow 檢定統計量\chi^2={(42-35.56)^2\over 35.56} +{(38-44.44)^2\over 44.44} +{(38-44.44)^2\over 44.44} +{(62-55.56)^2\over 55.56} \approx 3.8\\,故選\bbox[red,2pt]{(C)}$$
解答:$$均勻分配\Rightarrow 每組人數相等,均為150\div 3=50,故選\bbox[red,2pt]{(D)}$$
解答:$$\cases{總人數=450\\ 職級2的員工數=15+ 240+20 + 5=280 \\離婚人數=7+20+ 3=30} \\ \Rightarrow 離婚比例={30\over 450} \Rightarrow 職級2離婚人數之期望值=280\times {30\over 450} =18.667,故選\bbox[red,2pt]{(B)}$$
解答:$$期望值:\begin{array}{} 機票類似& 國內 & 國外\\\hline 頭等艙& 35 & 15\\ 商務艙& 150 & 66 \\ 經濟艙& 438 & 192\\\hline \end{array} \\ \Rightarrow 檢定統計量\chi^2 = {(28-35)^2\over 35} +{(22-15)^2\over 15} + {(95-150)^2\over 150} +{(121-66)^2 \over 66} +{(500-438)^2\over 438}\\\qquad + {(130-192)^2\over 192} \approx 99.5,故選\bbox[red,2pt]{(D)}$$
解答:$$五月的預估值F(5)=F(4)+0.4(221-F(4)) = 217+0.4(221-217)= 218.6\\ \Rightarrow F(6)=F(5)+0.4(216-F(5))=218.6+0.4(216-218.6)=217.56,故選\bbox[red,2pt]{(D)}$$
解答:$$期數越多代表被平均的數也越多,曲線變得更平緩,故選\bbox[red,2pt]{(B)}$$
解答:$${80分以上且來自A班\over 所有80分以上的人數}={50\times 12\% \over 50\times 12\% +70\times 10\%+ 80\times 15\%} ={6\over 6+7 + 12} ={6\over 25},故選\bbox[red,2pt]{(B)}$$
解答:$$A因子的自由度乘上B因子的自由度=(a-1)(b-1),故選\bbox[red,2pt]{(A)}$$
解答:$$SSE = MSE\times(n-2)=200\times 18= 3600 \Rightarrow SST= SSE+SSR = 3600+1600= 5200\\ \Rightarrow R^2 = 1-{SSE\over SST} =1-{36\over 52}=0.308,故選\bbox[red,2pt]{(C)}$$
解答:$$斜率={\sum(x-\bar x)(y-\bar y)\over \sum(x-\bar x)^2} ={2250\over 100\times (10-1)}=2.5;\\又迴歸直線經過(\bar x,\bar y),因此直線方程式為:y-\bar y=2.5(x-\bar x) \Rightarrow y-7.5=2.5(x-5)\\ \Rightarrow y=2.5x-5 \Rightarrow 截距為-5,故選\bbox[red,2pt]{(B)}$$
解答:$$判定係數R^2=0.81 \Rightarrow 相關係數 r=\pm \sqrt{0.81} =\pm 0.9\\ 又r={\text{cov}(x,y)\over S_x\cdot S_y} ={\text{cov}(x,y)\over \sqrt{1600}\cdot \sqrt{1225}} ={\text{cov}(x,y)\over 40\cdot 35} = 0.9 \Rightarrow \text{cov}(x,y)=1260,故選\bbox[red,2pt]{(A)}$$
解答:$$(\hat y(2)-8)^2 +(\hat y(1)-5)^2 +(\hat y(2)-7)^2 =(11-8)^2 +(6-5)^2 +(11-7)^2 = 9+1+16=26\\,故選\bbox[red,2pt]{(C)}$$
解答:$$迴歸直線斜率= 相關係數r\times {\sigma_y\over \sigma_x} \Rightarrow 4.568 = r\times {31.9043 \over 6.8336} \Rightarrow r= 0.9784 \\\Rightarrow R^2=r^2= 0.9573 ,故選\bbox[red,2pt]{(B)}$$
解答:$$連檢定\text{(Runs Test) 即是用來檢定樣本是否為隨機產生的};\\現在p=0.3685 \gt 5\% \Rightarrow 未達顯著,故選\bbox[red,2pt]{(A)}$$
解答:$$觀察值:\begin{array}{l|cc|r} & \lt 30 & \gt 30 & 小計\\\hline 職業婦女 & 42 & 38 & 80\\家庭主婦 & 38 & 62 & 100\\ \hdashline 小計 & 80 & 100 & 180\end{array} \\ \Rightarrow 期望值:\begin{array}{l|cc|r} & \lt 30 & \gt 30 & 小計\\\hline 職業婦女 & 80\cdot {4\over 9}=35.56 & 80\cdot {5\over 9}=44.44 & 80\\家庭主婦 & 100\cdot {4\over 9}=44.44 & 100\cdot {5\over 9}= 55.56& 100\\ \hdashline 小計 & 80 & 100 & 180\end{array}\\ \Rightarrow 檢定統計量\chi^2={(42-35.56)^2\over 35.56} +{(38-44.44)^2\over 44.44} +{(38-44.44)^2\over 44.44} +{(62-55.56)^2\over 55.56} \approx 3.8\\,故選\bbox[red,2pt]{(C)}$$
解答:$$均勻分配\Rightarrow 每組人數相等,均為150\div 3=50,故選\bbox[red,2pt]{(D)}$$
解答:$$\cases{總人數=450\\ 職級2的員工數=15+ 240+20 + 5=280 \\離婚人數=7+20+ 3=30} \\ \Rightarrow 離婚比例={30\over 450} \Rightarrow 職級2離婚人數之期望值=280\times {30\over 450} =18.667,故選\bbox[red,2pt]{(B)}$$
解答:$$期望值:\begin{array}{} 機票類似& 國內 & 國外\\\hline 頭等艙& 35 & 15\\ 商務艙& 150 & 66 \\ 經濟艙& 438 & 192\\\hline \end{array} \\ \Rightarrow 檢定統計量\chi^2 = {(28-35)^2\over 35} +{(22-15)^2\over 15} + {(95-150)^2\over 150} +{(121-66)^2 \over 66} +{(500-438)^2\over 438}\\\qquad + {(130-192)^2\over 192} \approx 99.5,故選\bbox[red,2pt]{(D)}$$
解答:$$五月的預估值F(5)=F(4)+0.4(221-F(4)) = 217+0.4(221-217)= 218.6\\ \Rightarrow F(6)=F(5)+0.4(216-F(5))=218.6+0.4(216-218.6)=217.56,故選\bbox[red,2pt]{(D)}$$
解答:$$期數越多代表被平均的數也越多,曲線變得更平緩,故選\bbox[red,2pt]{(B)}$$
解答:$${80分以上且來自A班\over 所有80分以上的人數}={50\times 12\% \over 50\times 12\% +70\times 10\%+ 80\times 15\%} ={6\over 6+7 + 12} ={6\over 25},故選\bbox[red,2pt]{(B)}$$


























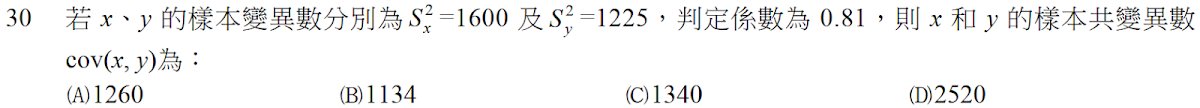








沒有留言:
張貼留言